Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 2 Lesson 2.2 Adding and Subtracting in Scientific Notation to finish your assignments.
Math in Focus Grade 8 Course 3 A Chapter 2 Lesson 2.2 Answer Key Adding and Subtracting in Scientific Notation
Math in Focus Grade 8 Chapter 2 Lesson 2.2 Guided Practice Answer Key
Complete.
Question 1.
The population of Washington, D.C., is about 5.9 • 105. South Dakota has a population of approximately 8 • 105.
a) Find the sum of the populations.
Sum of populations
= Population of Washington D.C. + Population of South Dakota
The sum of the populations is about 
.
Answer:
Sum of populations
= Population of Washington D.C. + Population of South Dakota
5.9 • 105 + 8 • 105.
Substitute the value 105. from each term
Add within the parentheses
(5.9 + 8) • 105.
13.9 • 105.
write 13.9 in the scientific notation.
1.39 • 101.• 105.
Use the product of powers property.
1.39 • 106.
b) Find the difference in the populations.
Difference in the populations
= Population of South Dakota – Population of Washington, D.C.
The difference in the populations is about .
Answer:
Population of South Dakota – Population of Washington, D.C.
8 • 105 – 5.9 • 105.
Substitute the value 105. from each term
Add within the parentheses
(8 – 5.9) • 105.
2.1 • 105.
write 13.9 in the scientific notation.
21 • 101.• 105.
Use the product of powers property.
21 • 106.
Question 2.
The approximate length of the smallest salamander is 1.7 • 10-2 meter. The smallest lizard is about 1.6 • 10-2 meter long.
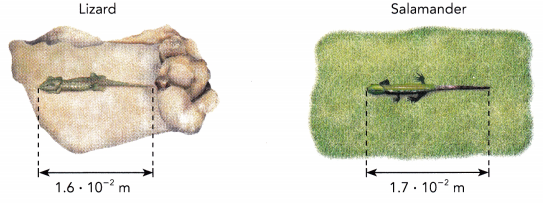
a) What is the sum of the lengths of the salamander and the lizard?
Sum of the lengths of the salamander and the lizard
= Length of salamander + Length of lizard
= 1.7 • 10-2 + 1.6 • 10-2 Substitute.
= ( + ) • Factor from each term.
= • m within parentheses.
The sum of the lengths is about meter.
Answer:
Sum of the lengths of the salamander and the lizard
= Length of salamander + Length of lizard
= 1.7 • 10-2 + 1.6 • 10-2 Substitute.
= (1.7 + 1.6) • 10-2
= (3.3)• 10-2
The sum of the lengths is about (3.3)• 10-2 meter.
b) What is the difference ¡n the length of the reptiles?
The salamander is about meter longer than the lizard.
Answer:
Difference in length between the salamander and lizard.
= Length of salamander – Length of lizard
= 1.7 • 10-2 – 1.6 • 10-2 Substitute.
= (1.7 – 1.6) • 10-2
= 0.1 • 10-2
= 1 • 10-1 • 10-2
= 1 • 10-3
Question 3.
The approximate area of the continent of Australia is 9 • 106 square kilometers.
The area of the continent of Antarctica is about 1,37 • 107 square kilometers.
a) Find the approximate sum of the land areas of the two continents.
The sum of the land areas is about square kilometers.
Answer:
Approximate sum of the land areas of the two continents
Area of Australia + Area of Antarctica
9 • 106 + 1.37 • 107
9 • 106 + 1.37 • 106 • 101
(9 + 13.7) • 106
22.7 • 106
2.27 • 107 square kilometers
b) What is the difference in the areas of the two continents?
Difference in the land areas
= Area of Antarctica – Area of Australia
The land area of Antarctica is about square kilometers larger than the land area of Australia.
Answer:
The difference in the land areas
= Area of Antarctica – Area of Australia
9 • 106 – 1.37 • 107
1.37 • 106 – 9 • 106
(13.7 – 9) • 106
4.7 • 106 square kilometers
Solve. Write your answers in scientific notation.
Question 4.
A custom-made invitation using a 10-pt card stock is about 2.54 • 10-4 meter thick. It is placed inside a tissue paper insert that is approximately 6.0 • 10-6 meter thick.
a) How thick is the invitation when placed in the tissue paper insert?
Answer:
2.54 • 10-4+ 6.0 • 10-6 meters thick
2.54 • 10-4+ 0.06 • 10-4 meters thick
(2.54 + 0.06) • 10-4 meters thick
2.6 • 10-4 meters
b) How much thicker is the invitation than the tissue paper insert?
Answer:
Let x is a variable here representing the number of times thicker.
Thickness of the card stock is x times as thick as tissue.
2.54 • 10-4= x • 6.0 • 10-6
x = 2.54 • 10-4/6.0 • 10-6
x = 0.423 • 102
x = 4.23 • 102
Complete.
Question 5.
On average, Pluto orbits the Sun at a distance of approximately 4,802 gigameters. Uranus’s average distance from the Sun is about 2.992 • 109 kilometers. Which planet is farther from the Sun? How much farther?
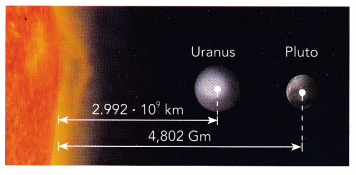
Distance of Pluto from the Sun:
Gm = • km Write in scientific notation.
Difference in distance of Pluto and Uranus from the Sun
= Distance of from the Sun – Distance of from the Sun
= • – • Substitute.
= ( – ) • Factor from each term.
= • km within parentheses.
So, is kilometers farther from the Sun.
Answer:
Given,
On average, Pluto orbits the Sun at a distance of approximately 4,802 gigameters.
Uranus’s average distance from the Sun is about 2.992 • 109 kilometers.
1 gigameter = 106 kilometers.
4,802 gigameters = 4,802 • 106 kilometers.
Difference in distance of Pluto and Uranus from the Sun
= Distance of Pluto from the Sun – Distance of Uranus from the Sun
4,802 • 106 kilometers – 2.992 • 109 kilometers
= 4,802 • 106 kilometers – 2,992 • 106 kilometers
= (4802 – 2992) • 106 kilometers
= 1810 • 106
So, Pluto is 1810 • 106 kilometers farther from the Sun.
Math in Focus Course 3A Practice 2.2 Answer Key
Solve. Show your work. Round the coefficient to the nearest tenth.
Question 1.
6.3 • 10-2 + 4.9 • 10-2
Answer:
(6.3 + 4.9) • 10-2
(11.2) • 10-2
Now, Round the coefficient to the nearest tenth.
11 • 10-2
Question 2.
7.2 • 102 – 3.5 • 102
Answer:
7.2 • 102 – 3.5 • 102
(7.2 – 3.5) • 102
3.7 • 102
Now, Round the coefficient to the nearest tenth.
4 • 102
Question 3.
3.8 • 103 + 5.2 • 104
Answer:
3.8 • 103 + 5.2 • 104
3.8 • 103 + 5.2 • 103 • 101
(3.8 + 52) • 103
55.8 • 103
Now, Round the coefficient to the nearest tenth.
56 • 103
Question 4.
8.1 • 105 – 2.8 • 104
Answer:
8.1 • 105 – 2.8 • 104
81 • 104 – 2.8 • 104
(81 – 2.8) • 104
78.2 • 104
Now, Round the coefficient to the nearest tenth.
78 • 104
Use the table to answer questions 5 to 9.
The table shows the amounts of energy, in Calories, contained in various foods.
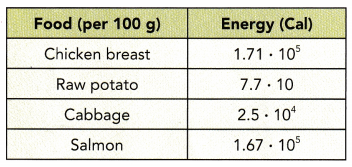
Question 5.
Find the total energy in each food combination. Write your answer in scientific notation. Round coefficients to the nearest tenth.
a) Chicken breast and cabbage
Answer:
Chicken breast: 1.71 • 104
cabbage: 2.5 • 104
Total energy in each food combination is
1.71 • 104 + 2.5 • 104
(1.7 + 2.5) • 104
4.2 • 104
4 • 104
b) Cabbage and raw potato
Answer:
cabbage: 2.5 • 104
Raw potato: 7.7 • 10
Total energy in each food combination is
2500 • 10 + 7.7 • 10
2507.7 • 10
2510 • 10
Question 6.
How many more Calories are in chicken breast than in salmon?
Answer:
Chicken breast: 1.71 • 104
Salmon: 1.67 • 105
1.67 • 105 – 1.71 • 104
(16.7 – 1.71) • 104
14.99 • 104
Question 7.
How many more Calories are in salmon than in cabbage?
Answer:
Salmon: 1.67 • 105
cabbage: 2.5 • 104
1.67 • 105 – 2.5 • 104
(16.7 – 2.5) • 104
14.2 • 104
Solve. Show your work.
Question 8.
A flight from Singapore to New York includes a stopover at Hawaii. The distance between Singapore and Hawaii is about 6.7 • 103 miles. The distance between New York and Hawaii is about 4.9 • 103 miles. Write each sum or difference in scientific notation.
a) Find the total distance from Singapore to New York.
Answer:
The distance between Singapore and Hawaii is about 6.7 • 103 miles.
The distance between New York and Hawaii is about 4.9 • 103 miles.
6.7 • 103 miles + 4.9 • 103 miles
(6.7 + 4.9) • 103 miles
11.6 • 103 miles
b) Find the difference in the length of the two flights.
Answer:
The distance between Singapore and Hawaii is about 6.7 • 103 miles.
The distance between New York and Hawaii is about 4.9 • 103 miles.
6.7 • 103 miles – 4.9 • 103 miles
(6.7 – 4.9) • 103 miles
1.8 • 103 miles
Question 9.
Angora wool, obtained from rabbits, has fibers with a diameter of about 1 • 10-6 meter. Cashmere, obtained from goats, has fibers with a diameter of about 1.45 • 10-5 meter. Write your answers in the appropriate unit in prefix form.
a) Find the sum of the diameters of the two types of fiber.
Answer:
Angora wool, obtained from rabbits, has fibers with a diameter of about 1 • 10-6 meter.
Cashmere, obtained from goats, has fibers with a diameter of about 1.45 • 10-5 meter.
1.45 • 10-5 meter + 1 • 10-6 meter.
14.5 • 10-6 meter + 1 • 10-6 meter.
(14.5 + 1) • 10-6 meter.
15.5 • 10-6 meter.
1.55 • 10-5 meter.
b) How much wider is the cashmere fiber than the angora fiber?
Answer:
Angora wool, obtained from rabbits, has fibers with a diameter of about 1 • 10-6 meter.
Cashmere, obtained from goats, has fibers with a diameter of about 1.45 • 10-5 meter.
1.45 • 10-5 meter – 1 • 10-6 meter.
14.5 • 10-6 meter – 1 • 10-6 meter.
(14.5 – 1) • 10-6 meter.
13.5 • 10-6 meter.
1.35 • 10-5 meter.
The average distances of three planets from the Sun are shown in the diagram. Use this information for questions 10 to 13. Express your answers in kilometers.
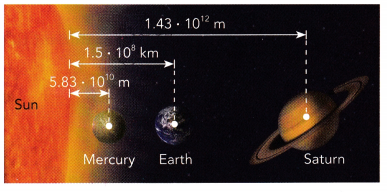
Question 10.
What is the closest Mercury comes to Earth when both are at an average distance from the Sun?
Answer:
Mercury: 5.83 • 1010
Earth: 1.5 • 108 km = 1.5 • 108 • 103 m = 1.5 • 1010• 101
Difference between the distance of Earth from Sun to distance of Mercury from Sun
15 • 1010 – 5.83 • 1010
(15 – 5.83) • 1010
9.17 • 1010
Question 11.
What is the closest Saturn comes to Mercury when both are at an average distance from the Sun?
Answer:
Mercury: 5.83 • 1010
Saturn: 1.43 • 1012
Difference between the distance of Saturn from Sun to distance of Mercury from Sun
143 • 1010 – 5.83 • 1010
(143 – 5.83) • 1010
137.17 • 1010
Question 12.
What is the closest Saturn comes to Earth when both are at an average distance from the Sun?
Answer:
Earth: 1.5 • 108 km = 1.5 • 108 • 103 m = 1.5 • 1011
Saturn: 1.43 • 1012
Difference between the distance of Saturn from Sun to distance of Mercury from Sun
14.3 • 1011 – 1.5 • 1011
(14.3 – 1.5) • 1011
12.8• 1011
Question 13.
Is the distance you found in 12 greater or less than the average distance from Earth to the Sun? Explain.
Answer: Yes the distance of Saturn from the Sun to the distance of Mercury from the Sun is 12.8• 1011
Solve. Show your work.
Question 14.
Factories A and B produce potato chips. They use the same basic ingredients: potatoes, oil, and salt. Last year, each factory used different amounts of these ingredients, as shown in the table.
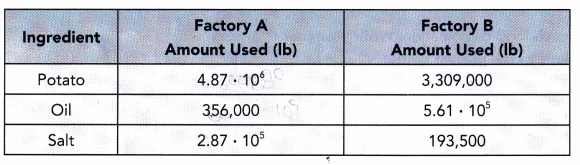
a) Which factory used more potatoes last year? How many more potatoes did it use?
Answer: By seeing the above table we can say that Factory A has used more potatoes last year than Factor B.
Potato Factory A Used: 4.87 • 106
Potato Factory B Used: 3,309 • 103
Potato Factory A Used: 4870 • 103
Potatoes Used Last Year: 4870 • 103– 3,309 • 103
(4870 – 3309) • 103
1561 • 103
b) Which factory used more oil last year? How much more oil did it use than the other factory?
Answer:
By seeing the above table we can say that Factory B has used more oil last year than Factor A.
Oil Factory A Used: 356,000 = 356 • 103
Oil Factory B Used: 5.61 • 105 = 561 • 103
Oil Used Last Year: 561 • 103– 356• 103
(561- 356) • 103
205• 103
c) Find the total weight of the ingredients used by each factory. Write your answer in scientific notation.
Answer:
Factory A:
Potato Factory A Used: 4870 • 103
Oil Factory A Used: 356,000 = 356 • 103
Salt Factory A Used: 2.87 • 105 = 287 • 103
4870 • 103 + 356 • 103 + 287 • 103
(4870 + 356 + 287) • 103
5513 • 103
Factory B:
Potato Factory B Used: 3,309 • 103
Oil Factory B Used: 561 • 103
Salt Factory B Used: 193500 = 193.5 • 103
3309 • 103 + 561 • 103 + 193.5 • 103
(3309+ 561 + 193.5) • 103
4063.5 • 103
Question 15.
Math journal The approximate population of the following countries in North America in 2011 are shown in the table. Explain how to use scientific notation to find the total population of the countries.
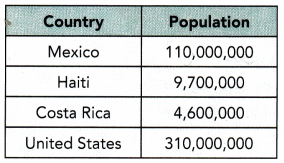
Answer:
Mexico: 110,000,000 = 11 • 107
Haiti: 9,700 000 = 97 • 105
Costa Rica: 4,600,000 = 46 • 105
United States: 310,000,000 = 31 • 107
11 • 107 + 31 • 107 + 97 • 105 + 46 • 105
4 • 107 + 143 • 105