Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems: Rates and Unit Rates

by

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 5 Lesson 5.2 Real-World Problems: Rates and Unit Rates to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 5 Lesson 5.2 Answer Key Real-World Problems: Rates and Unit Rates

Math in Focus Grade 6 Chapter 5 Lesson 5.2 Guided Practice Answer Key

Solve.

Question 1.
A unicycle wheel makes 196 revolutions in 7 minutes.
a) At this rate, how many revolutions does it make in 1 minute?
The unicycle wheel makes the same number of revolutions every minute.
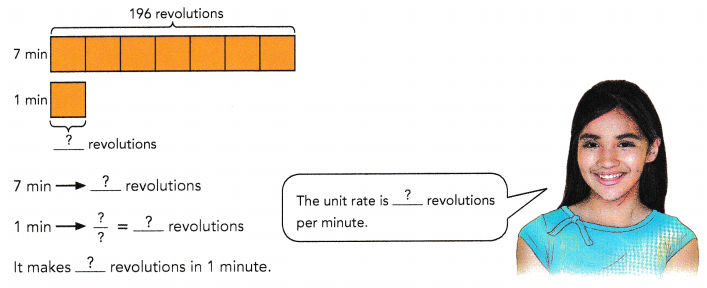
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 1
Answer:
28 revolutions
Explanation:

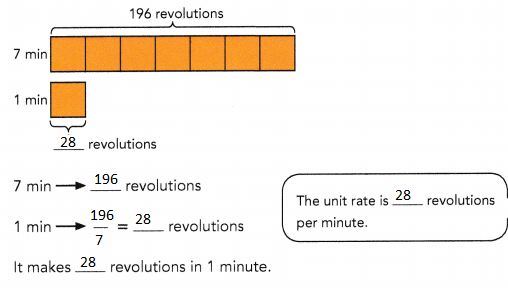
b) At this rate, how many revolutions does the unicycle wheel make in 15 minutes?
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 2
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 min → Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 × Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 = Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 revolutions
The unicycle makes Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 revolutions in 15 minutes.
Answer:
420 revolutions
Explanation:

15 min → 28 × 15 = 420 revolutions
The unicycle makes 420 revolutions in 15 minutes.

Question 2.
Megan babysits for 5 hours and earns $60.
a) At this rate, how much does she earn in 1 hour?
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 hours → $ Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
1 hour → $ Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 ÷ Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 = $Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
She earns $ Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 in 1 hour.
Answer:
$ 12 in 1 hour.
Explanation:
5 hours → $ 60
1 hour → $ 60 ÷ 5 = $12
She earns $ 12 in 1 hour.

b) At this rate, how much will Megan earn if she babysits for 14 hours?
14 hours → Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 × Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 = $Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
Megan will earn $ Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 if she babysits for 14 hours.
Answer:
$168 for 14 hours
Explanation:
14 hours → 14 × 12 = $168
Megan will earn $ 168 if she babysits for 14 hours.

Question 3.
The table shows the charges for renting a bicycle.
Tom rented a bicycle from 10 A.M. to 2 P.M. ON the same day. How much did he pay for renting the bicycle?
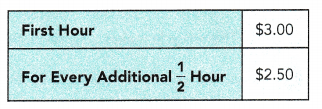
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 4
Total number of hours = Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 h
Charge for first hour = $Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
Charge for each additional 1 hour = 2 × Cost for each additional \(\frac{1}{2}\) hour
= 2 × $Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
= $Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
Charge for last three hours = Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 × $Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
= $Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
Total charge = $Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 + $Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
= $Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
Tom paid $Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 for renting the bicycle.
Answer:
$18
Explanation:
Total number of hours = 4 h
Charge for first hour = $3.00
Charge for each additional 1 hour = 2 × Cost for each additional \(\frac{1}{2}\) hour
= 2 × $2.5
= $5.0
Charge for last three hours = 3 × $5
= $15.00
Total charge = $3.00 + $15.00
= $18.00
Tom paid $18.00 for renting the bicycle.

Question 4.
Chloe scored 87 points in 5 basketball games, and Fiona scored 45 points in 2 basketball games. Which of the two players scored more points per game? Explain.
Chloe: .
5 games → Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 points
1 game → Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 ÷ 5 = Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 points
Chloe scored Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 points per game.

Fiona: .
2 games → Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 points
1 game → Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 ÷ Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 = Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 points
Fiona scored Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 points per game.

Comparing the number of points each player scored per game, Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 scored a higher number of points per game.
So, Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 scored more points per game.
Answer:
5.1 scored more points per game
Explanation:
Chloe: .
5 games → 87 points
1 game → 87 ÷ 5 = 17.4 points
Chloe scored 17.4 points per game.

Fiona: .
2 games → 45 points
1 game → 45 ÷ 2 = 22.5 points
Fiona scored 22.5 points per game.

Comparing the number of points each player scored per game, Fiona scored a higher number of points per game.
22.5 – 17.4 = 5.1
So, 5.1 scored more points per game.

Question 5.
A high-speed train can travel at a speed of 65 meters per second. How far can the train travel in 2 seconds?
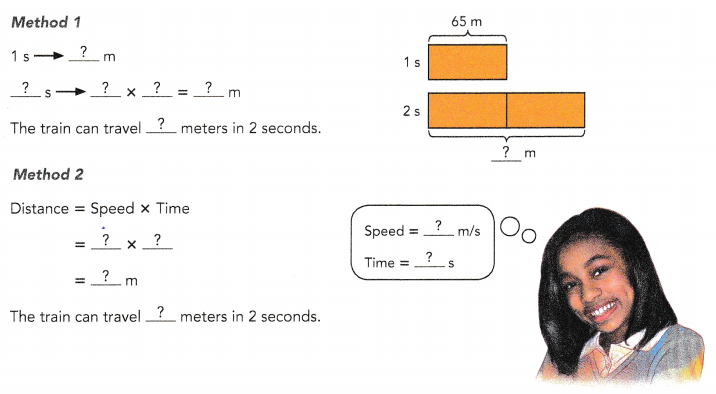
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 5
Answer:
130 M
Explanation:

Question 6.
The distance between City X and City Y is 216 kilometers. Mr. Thomas rides his motorcycle at a speed of 54 kilometers per hour. How long does he take to travel from City X to City Y?
Method 1
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 km → Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 h
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 km → \(\frac{?}{?}\) = Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 h
Mr. Thomas takes Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 hours to travel from City X to City Y.
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 6
Method 2
Time = Distance ÷ Speed
= Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 ÷ Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
= Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 h
Mr. Thomas takes Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 hours to travel from City X to City Y.
Answer:
4 hours
Explanation:
Method 1
216 km → Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 h
216 km → \(\frac{216}{54?}\) = 4 h
Mr. Thomas takes 4 hours to travel from City X to City Y.

Method 2
Time = Distance ÷ Speed
= 216 ÷ 54
= 4 h
Mr. Thomas takes 4 hours to travel from City X to City Y.

Question 7.
The distance between Town P and Town Q is 80 miles, and the distance between Town Q and Town R is 320 miles. A van takes 2\(\frac{1}{2}\) hours to travel from Town P to Town Q. It takes another 5 hours to travel from Town Q to Town R. Find the average speed of the van for the whole journey.
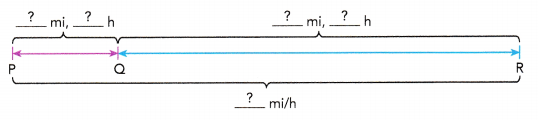
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 7
Total distance from Town P to Town R = 80 + Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
= Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 mi
Total time taken to travel from Town P to Town R = 2\(\frac{1}{2}\) + Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
= Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 h
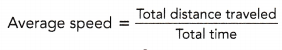
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 12
= \(\frac{?}{?}\)
= Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 ÷ Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
= Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 mi/h or Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 mph
The average speed of the van is Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 miles per hour.
Answer:
53.33 min/hr or 53 mph
Explanation:

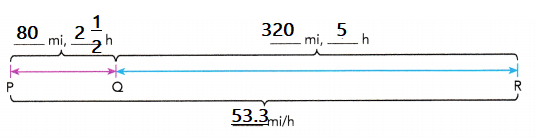
Total distance from Town P to Town R = 80 + 320 = 400 mi
Total time taken to travel from Town P to Town R = 2\(\frac{1}{2}\) + 5
= \(\frac{15}{2}\) h
=7\(\frac{1}{2}\) h
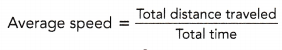
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 12
= \(\frac{?}{?}\)
= 400 ÷7 \(\frac{1}{2}\)
= 53.33 min/hr or 53 mph
The average speed of the van is 53.33 miles per hour.

Question 8.
Celia ran around a 400-meter track two times. It took her 4 minutes to run around the track once, and 6 minutes to run around it again. Find Celia’s average speed.
Total distance Celia ran = 2 × Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
= Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 m
Total time taken to run around the track twice = Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 + Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3
= Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 min
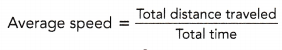
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 12
= \(\frac{?}{?}\)
= Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 m/min
Celia’s average speed was Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 3 meters per minute.
Answer:
80 meters per minute.
Explanation:
Total distance Celia ran = 2 × 400 = 800 m
Total time taken to run around the track twice = 4 + 6 = 10 min
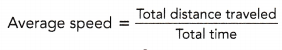
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 12
= \(\frac{800}{10}\)
= 80 m/min
Celia’s average speed was 80 meters per minute.

Math in Focus Course 1A Practice 5.2 Answer Key

Solve. Show your work.

Question 1.
A tennis ball machine can launch 60 tennis balls in 12 minutes. At this rate, how many tennis balls can it launch in 2 hours?
Answer:
600 Tennis balls
Explanation:
There are 120 minutes in 2 hours
10 sets of 12 minutes in 120 minutes.
\(\frac{120}{12}\) x 60 = 600
Therefore, 10 sets of 60 balls launched.

Question 2.
Water flows from a faucet at a rate of 5 liters every 25 seconds.
a) At this rate, how much water will flow from the faucet in 45 seconds?
Answer:
9 liters
Explanation:
The rate per 5 seconds, given in the first question is 45 seconds.
\(\frac{5}{25}\) = \(\frac{11}{5}\)
The x amount of liters in 45 seconds.
\(\frac{x}{45}\) = \(\frac{11}{5}\)
5x = 45
x = 9 liters

b) At this rate, how long will it take to collect 60 liters of water?
Answer:
300 seconds or 5 hours
Explanation:
9 liters for every 45 seconds.
60 liters in x amount of seconds.
\(\frac{60}{x}\) = \(\frac{11}{5}\)
x = 60 x 5
x = 300 sec

Question 3.
There are 1,600 kilocalories in the 5 cups of dog food that Mike gives his adult dog. Mike gives his puppy 2 cups of the same dog food. How many kilocalories are there in this 2-cup serving?
Answer:
640 kilocalories
Explanation:
There are 1,600 kilocalories in the 5 cups of dog food that Mike gives his adult dog.
Kilocalories = \(\frac{1,600}{5}\)
Mike gives his puppy 2 cups of the same dog food.
Total kilocalories are there in this 2-cup serving
Kilocalories = 320 per cup
Kilocalories for 2 cups = 320 x 2 = 640 for 2 cups

Question 4.
The table shows the postal charges for sending letters to Country Y. How much does it cost to send a letter weighing 60 grams to Country Y?
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 9
Answer:
$1.70
Explanation:
Cost of a letter weighing 60 grams to Country
first 20 g = 50 cents
next 40 g = 30 cents x 4 = 120 cents
weighing 60 grams to Country Y total  = 120 + 50
= 170 cents or $1.70

Question 5.
A vehicle traveled at a speed of 54 kilometers per hour for 3 hours. Find the distance traveled.
Answer:
162 kilometers
Explanation:
A vehicle traveled at a speed of 54 kilometers per hour
The distance traveled for 3 hours
1 hour = 54 kilometers
3 hours = 54 x 3 = 162 kmph.

Question 6.
A pigeon can fly at a speed of 84 kilometers per hour. How long does it take the pigeon to fly 7 kilometers?
Answer:
\(\frac{1}{12}\)minutes
Explanation:
A pigeon can fly at a speed of 84 kilometers per hour.
\(\frac{84}{1}\) = \(\frac{7}{x}\)
84x = 7
x = \(\frac{7}{84}\)
The distance taken by pigeon to fly 7 kilometers
= \(\frac{1}{12}\)

Question 7.
Karen walks home from school at a speed of 5 kilometers per hour. She takes 12 minutes to reach home. What is the distance between her school and her home? (Hint: Convert the time from minutes to hours.)
Answer:
1 kilometer
Explanation:
Distance = speed x time
= 5 x 12
=5 x 12/60 km
=60/60
=1 km

Question 8.
Kayla ran from her home to a beach at a speed of 6 meters per second. The distance from her home and the beach was 756 meters.
a) How long did she take to run from her home to the beach?
Answer:
126 seconds
Explanation:
Time = Distance ÷ Speed
Kayla ran from her home to a beach at a speed of 6 meters per second.
The distance from her home and the beach was 756 meters.
Distance = 756m
Speed= 6 meters per second
756m ÷ 6m/s = 126s

b) If Kayla wants to take 18 fewer seconds to reach the beach, at what speed must she run?
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 10
Answer:
7 meter per second
Explanation:
speed = Distance /time
= 756 / 108    (126 – 18 = 108sec)
= 7 m/s

Question 9.
Car A travels 702 miles on 12 gallons of gasoline. Car B travels 873 miles on 15 gallons of gasoline. David wants to buy a car with the lowest fuel consumption. Find out the distance traveled by each car per gallon of gasoline. Then tell which of the two cars, A, or B, David should buy.
Answer:
Car A
Explanation:
Car A travels 702 miles on 12 gallons of gasoline
= \(\frac{702}{12}\)
= 58.5 miles per gallon

Car B travels 873 miles on 15 gallons of gasoline
= \(\frac{873}{15}\)
= 58.2 miles of gallon
Car A,  David should buy.

Question 10.
Post A and Post B are 120 meters apart. Post B and Post C are 300 meters apart. Ben cycled from Post A to Post B in 15 seconds. Then he cycled from Post B to Post C in 55 seconds. Find Ben’s average speed for the distance from Post A to Post C.
Answer:
6 meters per second
Explanation:
Post A to B
= \(\frac{120}{15}\)
= 8m/s
Post B to C
= \(\frac{300}{55}\)
= 5.45 m/s
average speed for the distance from Post A to Post C.
\(\frac{8 + 5.45}{2}\)
= 6.72m/s

Question 11.
Mr. Alan drove for 2\(\frac{1}{5}\) hours at a speed of 70 kilometers per hour. He then drove another 224 kilometers. He took 5 hours for the whole journey. What was Mr. Alan’s average speed for the whole journey?
Answer:
57.4 KMPH
Explanation:
Mr. Alan drove for 2\(\frac{1}{5}\) hours at a speed of 70 kilometers per hour
Distance = speed x time
Speed = Distance /Time
= \(\frac{224}{5}\)
= 44.5 KMPH
Mr. Alan’s average speed for the whole journey
= (70 + 44.5)/2
= 57.4 KMPH

Question 12.
A family took 2 hours to drive from City A to City B at a speed of 55 miles per hour. On the return trip, due to a snowstorm, the family took 3 hours to travel back to City A.
a) How many miles did the family travel in all?
Answer:
220 miles
Explanation:
City A to B
Distance = Speed x time
= 55 x 2 = 110 km
Return journey from city B to A distance 110 km
Distance = Speed x time
110 = Speed x 3
Speed = 36.66 miles per hour

b) What was the average speed for the entire trip?
Answer:
44 miles per hour
Explanation:
Return journey from city B to A distance 110 km
Distance = Speed x time
110 = Speed x 3
Speed = 36.66 miles per hour
the average speed for the entire trip
(55 + 36.66)/2 = 45.83 miles per hour

Brain @ Work

Question 1.
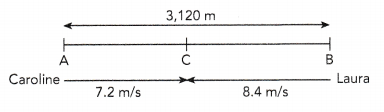
The distance between Point A and Point B is 3,120 meters. Caroline leaves Point A and Laura leaves Point B at the same time. The two girls cycle toward each other until they meet at Point C. Caroline’s speed is 7.2 meters per second, and Laura’s speed is 8.4 meters per second.
a) How long does Laura take to reach Point C?
Answer:
1,680 minutes
Explanation:
7.2 + 8.4 = 15.6 m/s
Time = Distance / Speed
= 3120/15.6
= 200 s
Laura take to reach Point C
Distance = Time x speed
= 200 x 8.4 = 1680 min

b) What is the distance between Point A and Point C?
Math in Focus Grade 6 Chapter 5 Lesson 5.2 Answer Key Real-World Problems Rates and Unit Rates 11
Answer:
Caroline leaves Point A
Explanation:
Distance from Point A to C
A = 3,120 and C = 1,680
3,120 – 1,680 = 1,440m

Leave a Comment