Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 7 Lesson 7.4 Expanding and Factoring Algebraic Expressions to score better marks in the exam.
Math in Focus Grade 6 Course 1 A Chapter 7 Lesson 7.4 Answer Key Expanding and Factoring Algebraic Expressions
Math in Focus Grade 6 Chapter 7 Lesson 7.4 Guided Practice Answer Key
Expand each expression.
Question 1.
3(x + 4)
Answer:
3x+12
Explanation:
3(x + 4)
= 3x + 3 x 4
= 3x + 12
Question 2.
6(2x + 3)
Answer:
12x + 18
Explanation:
6(2x + 3)
= 6 X 2x + 6 x 3
= 12x + 18
Question 3.
2(7 + 6x)
Answer: 14+ 12x
Explanation:
2(7 + 6x)
= 2 x 7 + 6x X 2
= 14 + 12x
Question 4.
5(y – 3)
Answer:
5y – 15
Explanation:
5(y – 3)
= 5y-15
Question 5.
4(4y – 1)
Answer:
16y – 4
Explanation:
4(4y – 1)
= 16y – 4
Question 6.
9(5x – 2)
Answer:
45x – 18
Explanation:
9(5x – 2)
= 9 x 5x – 2 x 9
= 45x – 18
State whether each pair of expressions are equivalent.
Question 7.
6(x + 5) and 6x + 30
Answer:
Yes, pair of expressions are equivalent
Explanation:
6(x + 5) and 6x + 30
6(x + 5) = 6x + 30
6(x + 5) and 6x + 30 are equal.
Question 8.
7(x + 3) and 21 + 7x
Answer:
Yes, pair of expressions are equivalent
Explanation:
7(x + 3) and 21 + 7x
7(x + 3) = 7x + 21
7x + 21 and 21 + 7x are equal.
Question 9.
4(y – 4) and 4y – 4
Answer:
NO, pair of expressions are not equivalent
Explanation:
4(y – 4) and 4y – 4
4(y – 4) = 4y – 16
4y – 16 is not equal to 4y – 4
Question 10.
3(y – 6) and 18 – 3y
Answer:
NO, pair of expressions are not equivalent
Explanation:
3(y – 6) and 18 – 3y
3(y – 6) = 3y – 18
3y – 18 is not equal to 18 – 3y
Hands-On Activity
Materials
- paper
- ruler
- scissors
RECOGNIZE THAT EXPANDED EXPRESSIONS ARE EQUIVALENT
STEP 1: Draw a rectangle that is 8 centimeters wide and more than 3 centimeters long on a piece of paper. Then cut out the rectangle.
Answer:
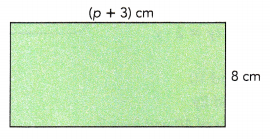
STEP 2: Find the area of the rectangle in terms of p.
Answer:
8p + 24 cm
Explanation:
Area of rectangle = Length x Breadth
= (p+3) x 8
= 8p + 24 cm
STEP 3: Then cut the rectangle into two rectangles A and B as shown.
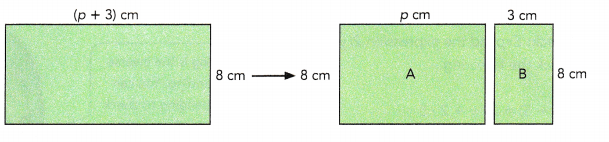
STEP 4: Find the areas of rectangle A and rectangle B.
Answer:
24cm
Explanation:
Area of rectangle A = Length x Breadth
= p x 8
= 8p cm
Area of rectangle B = Length x Breadth
= 3 x 8
= 24 cm
STEP 5: Using your answers found in STEP 2 and STEP 4, state how the three areas are related.
Answer:
8p + 24 cm
Explanation:
Area of rectangle = Area of rectangle A + Area of rectangle B
8p + 24 cm = 8p + 24 cm
STEP 6: You may repeat the activity using rectangles of other sizes.
can be done with different size of rectangles
Factor each expression.
Question 11.
3x + 3
Answer:
3,(x + 1)
Explanation:
In the above expression 3 is common factor.
3 and (x + 1) are the factors of 3x + 3
Question 12.
4x + 6
Answer:
2 and (2x + 3)
Explanation:
In the above expression 2 is common factor.
2,(2x + 3) are the factors of 4x + 6
Question 13.
8 + 6y
Answer:
2 and (4 + 3y)
Explanation:
8+6y
In the above expression 2 is common factor.
2 and (4 + 3y) are the factors of 8 + 6y
Question 14.
5y – 10
Answer:
5, (y-2)
Explanation:
In the above expression 5 is common factor.
5y – 10 = 5(y – 2)
Question 15.
4 – 10z
Answer:
2(2 – 5z)
Explanation:
In the above expression 2 is common factor.
4 – 10z = 2(2 – 5z)
Question 16.
12 – 8x
Answer:
4, (3-2x)
Explanation:
In the above expression 4 is common factor.
12 – 8x = 4(3 – 2x)
Question 17.
8f + 6
Answer:
2 ,(4f+3)
Explanation:
In the above expression 2 is common factor.
8f + 6 = 2(4f + 3)
Question 18.
12t – 8
Answer:
4,(3f – 2)
Explanation:
In the above expression 4 is common factor.
12t – 8 = 4(3f – 2)
Question 19.
15 + 5q
Answer:
5, (3+q)
Explanation:
In the above expression 5 is common factor.
15 + 5q = 5(3 + q)
Question 20.
32m – 40
Answer:
8 and (4m-5)
Explanation:
In the above expression 8 is common.
8 and (4m – 5)are the factors of 32m – 40
State whether each pair of expressions are equivalent.
Question 21.
8x + 6 and 2(4x + 3)
Answer:
Yes, pair of expressions are equivalent.
Explanation:
8x + 6 and 2(4x + 3)
8x + 6 = 2(4x + 3)
2(4x + 3) and 2(4x + 3) are equal.
Question 22.
3(y + 6) and 18 + 3y
Answer:
Yes, pair of expressions are equivalent.
Explanation:
3(y + 6) and 18 + 3y
3(y + 6) = 3y + 18
3y + 18 = 18 + 3y are equal.
Question 23.
5x – 10 and 5(x – 5)
Answer:
No, pair of expressions are not equivalent.
Explanation:
5x – 10 and 5(x – 5)
5x – 10 = 5(x – 2)
5(x – 2) and 5(x – 5) are not equal.
Question 24.
4(y – 4) and 16 – 4y
Answer:
No, pair of expressions are not equivalent.
Explanation:
4(y – 4) and 16 – 4y
4(y – 4) = 4y – 16
4y – 16 is not equivalent to 16 – 4y
4(y – 4) and 16 – 4y are not equivalent.
Question 25.
3(x + 5) and 15 + 3x
Answer:
Yes, pair of expressions are not equivalent.
Explanation:
3(x + 5) and 15 + 3x
3(x + 5) = 3x + 15
3x + 15 is equal to 15 + 3x
3(x + 5) and 15 + 3x are equivalent expressions.
Question 26.
12 – 8y and 4(2y – 3)
Answer:
No, pair of expressions are not equivalent.
Explanation:
12 – 8y and 4(2y – 3)
12 – 8y = 4(3 – 2y)
12 – 8y and 4(2y – 3) are not equivalent.
Math in Focus Course 1A Practice 7.4 Answer Key
Expand each expression.
Question 1.
5(x + 2)
Answer:
5x + 10
Explanation:
5(x + 2)
= 5 X x + 5 X 2
= 5x + 10
Question 2.
7(2x – 3)
Answer:
14x – 21
Explanation:
7(2x – 3)
= 7 X 2x – 7 X 3
= 14x – 21
Question 3.
4(y – 3)
Answer:
4y – 12
Explanation:
4(y – 3)
= 4 X y – 4 X 3
= 4y – 12
Question 4.
8(3y – 4)
Answer:
24y – 32
Explanation:
8(3y – 4)
= 8 X 3y – 8 X 4
= 24y – 32
Question 5.
3(x+ 11)
Answer:
3x + 33
Explanation:
3(x+ 11)
= 3 X x + 3 X 11
= 3x + 33
Question 6.
9(4x – 7)
Answer:
36x – 63
Explanation:
9(4x – 7)
= 9 X 4x – 9 X 7
= 36 x – 63
Factor each expression.
Question 7.
6p + 6
Answer:
6 , (p + 1)
Explanation:
6p + 6
Take 6 as common factor
6 (p + 1)
6, (p + 1) are the factors of 6p + 6
Question 8.
3p + 18
Answer:
3, (p + 6)
Explanation:
3p + 18
Take 3 as common factor
3 (p + 6)
3, (p+6) are the factors of 3p + 18
Question 9.
12 + 3q
Answer:
3, (4 + q)
Explanation:
12 + 3q
Take 3 as common factor
3 (4 + q)
3, (4 + q) are the factors of 12 + 3q
Question 10.
4w – 16
Answer:
4, (w – 4)
Explanation:
4w – 16
take 4 as common factor,
4 (w – 4)
4, (w – 4) are the factors of 4w – 16
Question 11.
14r – 8
Answer:
2, (7r – 4)
Explanation:
14r – 8
take 2 as common factor,
2 (7r – 4)
2, (7r – 4) are the factors of 14r – 8
Question 12.
12r – 12
Answer:
12, (r – 1)
Explanation:
12r – 12
take 12 as common factor,
12 (r – 1)
12, (r – 1) are the factors of 12r – 12
State whether each pair of expressions are equivalent.
Question 13.
4x + 12 and 4(x + 3)
Answer:
YES, pair of expressions are equivalent
Explanation:
4x + 12 and 4(x + 3)
4x + 12 and 4x + 12
both are equal
Question 14.
5(x – 1) and 5x – 1
Answer:
NO, pair of expressions are not equivalent
Explanation:
5(x – 1) and 5x – 1
5x – 5 and 5x – 1
both are not equal
Question 15.
7(5 + y) and 7y + 35
Answer:
YES, pair of expressions are equivalent
Explanation:
7(5 + y) and 7y + 35
35 + 7y and 7y + 35
both are equal
Question 16.
9(y – 2) and 18 – 9y
Answer:
NO, pair of expressions are not equivalent
Explanation:
9(y – 2) and 18 – 9y
9y – 18 and 18 – 9y
both are not equal
Expand and simplify each expression.
Question 17.
3(m + 2) + 4(6 + m)
Answer:
7m + 30
Explanation:
3(m + 2) + 4(6 + m)
= 3m + 6 + 24 +4m
= 7m + 30
Question 18.
5(2p + 5) + 4(2p – 3)
Answer:
18p+13
Explanation:
5(2p + 5) + 4(2p – 3)
= 10p + 25 + 8p – 12
= 18p + 13
Question 19.
4(6k + 7)+ 9 – 14k
Answer:
10k + 37
Explanation:
4(6k + 7)+ 9 – 14k
= 24k + 28 + 9 – 14k
= 10k + 37
Simplify each expression. Then factor the expression.
Question 20.
14x + 13 – 8x – 1
Answer:
6, (x+2)
Explanation:
14x + 13 – 8x – 1
= 14x – 8x + 13 – 1
= 6x + 12
= 6(x + 2)
6, (x + 2) are the factors of 14x + 13 – 8x – 1
Question 21.
8(y + 3) + 6 – 3y
Answer:
5, (y+6)
Explanation:
8(y + 3) + 6 – 3y
= 8y + 24 + 6 – 3y
= 8y – 3y + 24 + 6
= 5y + 30
= 5(y + 6)
5, (y + 6) are the factors of the 8(y + 3) + 6 – 3y
Question 22.
4(3z + 7) + 5(8 + 6z)
Answer:
2 , (21z+34)
Explanation:
4(3z + 7) + 5(8 + 6z)
= 12z + 28 + 40 + 30z
= 12z + 30z + 40 + 28
= 42z + 68
= 2 (21z + 34)
2 , (21z + 34) are the factors of 4(3z + 7) + 5(8 + 6z)
Solve.
Question 23.
Expand and simplify the expression 3(x – 2) + 9(x + 1) + 5(1 + 2x) + 2(3x – 4).
Answer:
28x
Explanation:
3(x – 2) + 9(x + 1) + 5(1 + 2x) + 2(3x – 4).
= 3x – 6 + 9x + 9 + 5 + 10x + 6x – 8.
= 3x + 9x + 10x + 6x – 6 +9 +5 – 8
= 28x + 0
= 28x
Question 24.
Are the two expressions equivalent? Justify your reasoning.
15(y + 6) + 10(y – 5) + 20(2y + 3)and 5(20 + 13y)
Answer:
Yes, the two expressions equivalent
Explanation:
15(y + 6) + 10(y – 5) + 20(2y + 3) and 5(20 + 13y)
= 15(y + 6) + 10(y – 5) + 20(2y + 3) and 5(20 + 13y)
= 15y + 90 + 10y – 50 +40y + 60 and 100 + 65y
= 65y + 100 and 100 + 65y
So, both are same.
Question 25.
A yard of lace costs w cents and a yard of fabric costs 40c more than the lace. Kimberly wants to buy one yard of lace and 2 yards of fabric. How much money will she need? Express your answer in terms of w.
Answer:
$80 w cents
Explanation:
cost of one yard of lace = w cents
cost of 2 yards of fabric = 2 × 40 = $80
Therefore, the total money needed is $80 + w cents
= $80 w cents
Question 26.
The average weight of 6 packages ¡s (9m + 8) pounds. 2 more packages, with weights of (12m + 1 2) pounds and (14m + 12) pounds, are added to the original 6 packages. Find the average weight of the 8 packages.
Answer:
10m + 9
Explanation:
9m + 8 is the average weight of the 6 packages = 54m + 48
12m + 12 and 14m + 12 is added
12m+12+14m+12 = 26m + 24
26m + 24 is added to the 54m + 48
= 54m + 26m + 48 + 24
= 80m + 72
the average weight of the 8 packages is = (80m + 72)/8 = 10m + 9
Question 27.
The figure shows two rectangles joined to form rectangle ABCD.
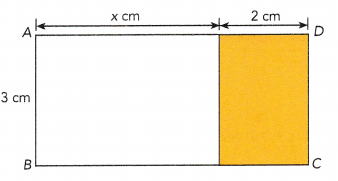
a) Write the length of \(\overline{B C}\) in terms of x. Then write an expression for the area of the rectangle ABCD in terms of x.
Answer:
Area =3x + 6 cm
Explanation:
the length of \(\overline{B C}\) in terms of x = x + 2
an expression for the area of the rectangle ABCD in terms of x
= x + 2 X 3
= (x + 2)3
= 3x + 6cm
b) Write an expression for the area of each of the two smaller rectangles.
Answer:
6 cm
Explanation:
the area of each of the two smaller rectangles
= 2 x 3 = 6cm
c) Math Journal Explain how you can use your answers in a) and b) to show that the following expressions are equivalent. 3x + 6 and 3(x + 2)
Answer:
Yes, both are equivalent
Explanation:
3x + 6 and 3(x + 2)
3(x + 2) can be written as 3x + 6
So, both are equal.