Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 7 Lesson 7.2 Evaluating Algebraic Expressions to score better marks in the exam.
Math in Focus Grade 6 Course 1 A Chapter 7 Lesson 7.2 Answer Key Evaluating Algebraic Expressions
Math in Focus Grade 6 Chapter 7 Lesson 7.2 Guided Practice Answer Key
Evaluate each algebraic expression for the given value of x.
Question 1.
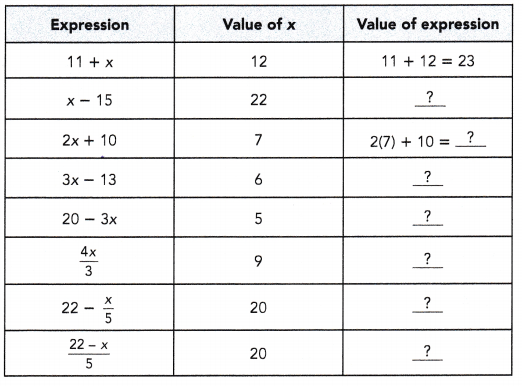
Answer:
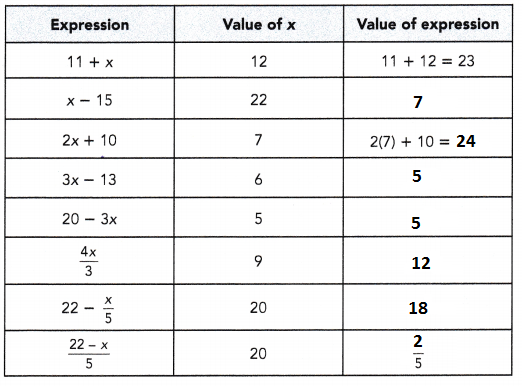
Explanation:
An expression is a term in that describes a group of variables, numbers and operators.
Operators include division, multiplication, addition and subtraction.
Variables in expression are usually denoted as x and y, but it can be and other symbol.
The expressions can be written as verbal phrase or algebraic expression.
Math in Focus Course 1A Practice 7.2 Answer Key
Evaluate each expression for the given value of the x.
Question 1.
x + x + 5 when x = 7
Answer:
19
Explanation:
x = 7
by substituting x value as 7
x + x + 5 = 7 + 7 + 5 = 19
Question 2.
3x + 5 when x = 5
Answer:
20
Explanation:
3x + 5, where as
x = 5
by substituting x value =5
3 x 5 + 5 = 15 + 5 = 20
Question 3.
5y – 8 when y = 3
Answer:
7
Explanation:
5 x y – 8
y = 3
by substituting y value = 3
5 x 3 – 8
15 – 8 = 7
Question 4.
40 – 9y when y = 2
Answer:
22
Explanation:
40 – 9y
y = 2
by substituting y value = 2
40 – 9 x 2 = 40 – 18 = 22
Question 5.
33 – 7w + 6 when w = 4
Answer:
19
Explanation:
33 – 7w + 6
w = 4
by substituting w value = 4
33 – 7 x 4 = 33 – 14 = 19
Question 6.
\(\frac{7w}{2}\) when w = 18
Answer:
63
Explanation:
= \(\frac{7w}{2}\)
w = 18
by substituting w value = 18
= \(\frac{7 x 18}{2}\)
= \(\frac{126}{2}\) = 63
Question 7.
4 + \(\frac{5z}{6}\) when z = 12
Answer:
14
Explanation:
4 + \(\frac{5z}{6}\)
z = 12
by substituting z value = 12
= 4 + \(\frac{5×12}{6}\)
= 4 + \(\frac{60}{6}\)
= 4+10 = 14
Question 8.
\(\frac{4+5z}{2}\) when z = 12
Answer:
32
Explanation:
\(\frac{4+5z}{2}\)
z = 12
by substituting z value =12
= \(\frac{4+5 x 12}{2}\)
= \(\frac{4+60}{2}\)
= \(\frac{64}{2}\) = 32
Question 9.
20 – \(\frac{4r}{5}\) when r = 10
Answer:
16
Explanation:
20 – \(\frac{4r}{5}\)
r = 10
by substituting r value =10
= 20 – \(\frac{4x 10}{5}\)
= 20 – \(\frac{40}{5}\)
= 20 – 8 = 16
Question 10.
\(\frac{8r}{9}\) – 15 when r = 27
Answer:
9
Explanation:
\(\frac{8r}{9}\) – 15
r = 27
by substituting r value =27
= \(\frac{8 x 27}{9}\) – 15
= \(\frac{216}{9}\) – 15
24 – 15 = 9
Question 11.
16 – \(\frac{2 z-4}{3}\) when z = 18
Answer:
\(\frac{16}{3}\)
Explanation:
16 – \(\frac{2 z-4}{3}\) when z = 18
by substituting z value = 18
16 – \(\frac{2 z-4}{3}\)
=16 – \(\frac{2 x 18 – 4}{3}\)
=16 – \(\frac{36-4}{3}\)
=16 – \(\frac{32}{3}\)
=\(\frac{48-32}{3}\)
\(\frac{16}{3}\)
Question 12.
16 – \(\frac{2 z}{3}\) – 4 when z = 18
Answer:
0
Explanation:
16 – \(\frac{2 z}{3}\) – 4 when z = 18
by substituting z value = 18
16 – \(\frac{2 x 18}{3}\) – 4
= 16 – \(\frac{36}{3}\) – 4
=16 – 12 – 4
=0
Evaluate each expression when x = 3.
Question 13.
\(\frac{x+1}{2}\) + \(\frac{5 x-3}{10}\)
Answer:
\(\frac{16}{5}\)
Explanation:
by substituting x value = 3 in the given algebraic equation
\(\frac{x+1}{2}\) + \(\frac{5 x-3}{10}\)
= \(\frac{3+1}{2}\) + \(\frac{5 x 3 – 3}{10}\)
= \(\frac{4}{2}\) + \(\frac{12}{10}\)
= 2 + \(\frac{6}{5}\)
= \(\frac{10 + 6}{5}\)
= \(\frac{16}{5}\)
Question 14.
\(\frac{11+x}{2}\) – \(\frac{9 x-3}{4}\)
Answer:
1
Explanation:
by substituting x value = 3 in the given algebraic equation
\(\frac{11+x}{2}\) – \(\frac{9 x-3}{4}\)
= \(\frac{11+3}{2}\) – \(\frac{9 x 3-3}{4}\)
= \(\frac{14}{2}\) – \(\frac{27-3}{4}\)
= \(\frac{7}{1}\) – \(\frac{24}{4}\)
7 – 6 = 1
Question 15.
\(\frac{7 x-6}{3}\) + 4(8 + 2x)
Answer:
61
Explanation:
by substituting x value = 3 in the given algebraic equation
\(\frac{7 x-6}{3}\) + 4(8 + 2x)
= \(\frac{7 x 3 -6}{3}\) + 4(8 + 2 x 3)
= \(\frac{21- 6}{3}\) + 4(8 + 6)
= \(\frac{15}{3}\) + 56
= 5 + 56
= 61
Question 16.
13(11 – 3x) – \(\frac{5(16-4 x)}{2}\)
Answer:
16
Explanation:
by substituting x value = 3 in the given algebraic equation
13(11 – 3x) – \(\frac{5(16-4 x)}{2}\)
13(11 – 3 x 3) – \(\frac{5(16-4 x 3)}{2}\)
13(11 – 9) – \(\frac{5(16 – 12)}{2}\)
13(2) – \(\frac{5(4)}{2}\)
26 – \(\frac{20}{2}\)
= 26 – \(\frac{20}{2}\)
= 26 – 10
= 16
Question 17.
5(x + 2) + 2(6 – x) + \(\frac{2 x+3}{3}\)
Answer:
34
Explanation:
by substituting x value = 3 in the given algebraic equation
5(x + 2) + 2(6 – x) + \(\frac{2 x+3}{3}\)
5(3 + 2) + 2(6 – 3) + \(\frac{2 x 3+3}{3}\)
5(5) + 2(3) + \(\frac{6+3}{3}\)
25 + 6 + 3 = 34
Question 18.
\(\frac{5 x-3}{4}\) + \(\frac{5(x+5)}{8}\) + 3(13 – 2x)
Answer:
29
Explanation:
by substituting x value = 3 in the given algebraic equation
\(\frac{5 x-3}{4}\) + \(\frac{5(x+5)}{8}\) + 3(13 – 2x)
= \(\frac{5 x 3 – 3}{4}\) + \(\frac{5(3+5)}{8}\) + 3(13 – 2 x 3)
= \(\frac{15-3}{4}\) + \(\frac{5(8)}{8}\) + 3(13 – 6)
= \(\frac{12}{4}\) + \(\frac{40}{8}\) + 3(7)
= 3 + 5 + 21
= 29
Question 19.
\(\frac{2 x+4}{5}\) – \(\frac{x+1}{4}\) + \(\frac{x}{6}\)
Answer:
\(\frac{3}{2}\)
Explanation:
by substituting x value = 3 in the given algebraic equation
\(\frac{2 x+4}{5}\) – \(\frac{x+1}{4}\) + \(\frac{x}{6}\)
= \(\frac{2 x 3+4}{5}\) – \(\frac{3+1}{4}\) + \(\frac{3}{6}\)
= \(\frac{10}{5}\) – \(\frac{4}{4}\) + \(\frac{1}{2}\)
= 2-1+\(\frac{1}{2}\)
=1+\(\frac{1}{2}\)
= \(\frac{3}{2}\)
Question 20.
7x – \(\frac{x}{5}\) + \(\frac{7-x}{9}\)
Answer:
21 – \(\frac{3}{5}\) + \(\frac{4}{9}\)
Explanation:
by substituting x value = 3 in the given algebraic equation
7x – \(\frac{x}{5}\) + \(\frac{7-x}{9}\)
= 7 x 3 – \(\frac{3}{5}\) + \(\frac{7-3}{9}\)
= 21 – \(\frac{3}{5}\) + \(\frac{4}{9}\)
= 21 – \(\frac{3}{5}\) + \(\frac{4}{9}\)
Evaluate each of the following when y = 7.
Question 21.
(5y + 2) minus (2y + 5).
Answer:
18
Explanation:
by substituting y value = 7 in the given algebraic equation
(5y + 2) minus (2y + 5)
= (5 x 7 + 2) – (2 x 7 + 5).
= (35 + 2) – (14 + 5).
= 37 – 19
= 18
Question 22.
The sum of \(\frac{y}{3}\) and \(\frac{4y}{9}\)
Answer:
\(\frac{49}{9}\)
Explanation:
by substituting y value = 7 in the given algebraic equation
\(\frac{y}{3}\) + \(\frac{4y}{9}\)
= \(\frac{7}{3}\) + \(\frac{4 x 7}{9}\)
= \(\frac{7}{3}\) + \(\frac{28}{9}\)
= \(\frac{21+28}{9}\)
= \(\frac{49}{9}\)
Question 23.
The product of (y + 1)and(y – 1)
Answer:
\(\frac{4}{3}\)
Explanation:
by substituting y value = 7 in the given algebraic equation
(y + 1)and(y – 1)
= (7 + 1)and(7 – 1)
= (8)and(6)
= \(\frac{8}{6}\)
= \(\frac{4}{3}\)
Question 24.
8(2y – 1) minus \(\frac{14 y+37}{5}\)
Answer:
8(2y – 1) minus \(\frac{14 y+37}{5}\)
Explanation:
by substituting y value = 7 in the given algebraic equation
8(2y – 1) minus \(\frac{14 y+37}{5}\)
= 8(2 X 7 – 1) minus \(\frac{14 X 7 + 37}{5}\)
= 8(2y – 1) minus \(\frac{14 y+37}{5}\)
Question 25.
The quotient of 9(7y – 15) and \(\frac{110-6 y}{4}\)
Answer:
18
Explanation:
by substituting y value = 7 in the given algebraic equation
9(7y – 15) and \(\frac{110-6 y}{4}\)
= 9(7 x 7 – 15) and \(\frac{110 – 6 x 7}{4}\)
= 9(49 – 15) and \(\frac{110-42}{4}\)
= 9(34) and \(\frac{68}{4}\)
= 306/17 = 18
Question 26.
The sum of \(\frac{5 y}{6}\) and 4(\(\frac{3 y}{7}\) + 2y)
Answer:
\(\frac{443}{6}\)
Explanation:
by substituting y value = 7 in the given algebraic equation
\(\frac{5 y}{6}\) and 4(\(\frac{3 y}{7}\) + 2y)
= \(\frac{5 x 7}{6}\) and 4(\(\frac{3 x 7}{7}\) + 2 x 7)
= \(\frac{35}{6}\) and 4(\(\frac{21}{7}\) + 14)
= \(\frac{35}{6}\) and 4(3 + 14)
= \(\frac{35}{6}\) +68
= \(\frac{35 + 408 }{6}\)
= \(\frac{443}{6}\)
Question 27.
The quotient of (\(\frac{y}{2}+\frac{2 y}{3}\)) and (\(\frac{5 y}{6}-\frac{y}{3}\))
Answer:
\(\frac{7}{3}\)
Explanation:
by substituting y value = 7 in the given algebraic equation
(\(\frac{y}{2}+\frac{2 y}{3}\)) and (\(\frac{5 y}{6}-\frac{y}{3}\))
= (\(\frac{7}{2}+\frac{2 x 7}{3}\)) and (\(\frac{5 x 7}{6}-\frac{7}{3}\))
= (\(\frac{7}{2}+\frac{14}{3}\)) and (\(\frac{35}{6}-\frac{7}{3}\))
= (\(\frac{21 + 28}{6}\)) and (\(\frac{35 – 14}{6}\))
= (\(\frac{49}{6}\)) and (\(\frac{21}{6}\))
= (\(\frac{49}{6}\)) X (\(\frac{6}{21}\))
= \(\frac{49}{21}\)
= \(\frac{7}{3}\)