Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 7 Lesson 7.5 Real-World Problems: Algebraic Expressions to score better marks in the exam.
Math in Focus Grade 6 Course 1 A Chapter 7 Lesson 7.5 Answer Key Real-World Problems: Algebraic Expressions
Math in Focus Grade 6 Chapter 7 Lesson 7.5 Guided Practice Answer Key
Complete.
Question 1.
Raoul is y years old. Kayla is 6 years older than Raoul and Isaac is 4 years younger than Raoul.
a) Find Kayla’s age.
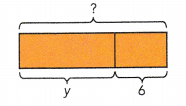
Kayla is 
years old.
Answer:
y + 6 years
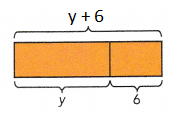
Explanation:
Raoul is y years old.
Kayla is 6 years older than Raoul and Isaac is 4 years younger than Raoul.
So, Kayla is y + 6 years old.
b) Find Isaac’s age.
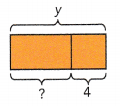
Isaac is years old.
Answer:
y – 4 years
Explanation:
Raoul is y years old.
Kayla is 6 years older than Raoul and Isaac is 4 years younger than Raoul.
So, Isaac is y – 4 years old.
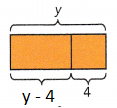
c) If y = 12, find the sum of Raoul’s age and Isaac’s age.
When y =12,
Isaac’s age:
– = –
= years old
Sum of Raoul’s age and Isaac’s age:
+ =
The sum of Roul’s age and Isaac’s age is years.
Answer:
20 years.
Explanation:
When y =12,
Isaac’s age:
12 – 4 = 8 years old
Sum of Raoul’s age and Isaac’s age:
12 + 8 = 20
The sum of Roul’s age and Isaac’s age is 20 years.
Question 2.
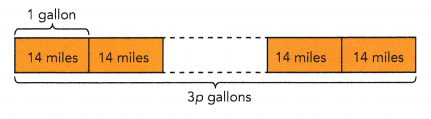
A pickup truck uses 1 gallon of gas for every 14 miles traveled,
a) How far can it travel on 3p gallons of gas?
1 gallon → miles
3p gallons → • = miles
It can travel miles on 3p gallons of gas.
Answer:
42 miles
Explanation:
1 gallon → 14 miles
3p gallons → 3p • 14 = 42 p miles
It can travel 42 p miles on 3p gallons of gas.
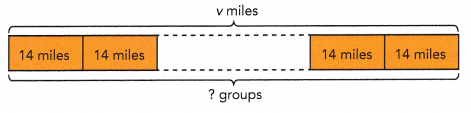
b) How many gallons of gas have been used after the pickup truck has traveled v miles? Evaluate this expression when v = 56.
14 miles → gallon
v miles → ÷ = gallons
gallons have been used.
When v = 56,
=
=
Answer:
4 groups
Explanation:
14 miles → 4 gallon
v miles → 56 ÷ 14 = 4 gallons
4 gallons have been used.
When v = 56,
56 = 14 x 4
= 4 groups
Question 3.
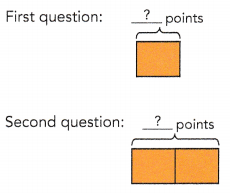
There were three questions in a mathematics test. Salma earned m points for the first question and twice the number of points for the second question,
a) How many points did she earn for the first two questions?
+ =
She earned points for the first two questions.
Answer:
3m points
Explanation:
m + 2m = 3m
She earned 3m points for the first two questions.
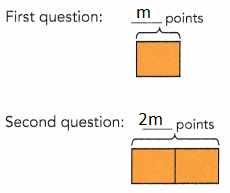
b) If she received a total of 25 points on the test, how many points did she earn for the third question?
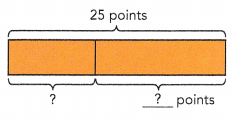
She earned points for the third question.
Answer:
10 points
Explanation:
Salma received a total of 25 points on the test,
Third question: 25 – 3m = 25 – (3 •5)
= 25 – 15
= 10
c) If m = 5, find the points she earned for each question.
First question: m = 5
Second question: 2m = 2 •
=
Third question: 25 – 3m = 25 – (3 • )
= 25 –
=
She earned points for the first question, points for the second question and points for the third question.
Answer:
10 points
Explanation:
First question: m = 5
Second question: 2m = 2 • 5 = 10
Third question: 25 – 3m = 25 – (3 •5)
= 25 – 15
= 10
She earned 5 points for the first question, 10 points for the second question and 10 points for the third question.
Math in Focus Course 1A Practice 7.5 Answer Key
Question 1.
Jenny is x years old. Thomas is 3 times as old as she is. Jenny is 5 years older than Alexis.
a) Find Alexis’s age in terms of x.
Answer:
x+5
Explanation:
Jenny age x years
Thomas age 3x
Alexis are x + 5
b) Find Thomas’s age in terms of x.
Answer: 3x
Explanation:
Jenny is x years old.
Thomas is 3 times as old as she is.
Thomas age 3x.
c) If x = 12, how much older is Thomas than Jenny?
Answer:
36 years
Explanation:
Thomas is 3x = 3(12) = 36 years
Question 2.
A van travels from Town A to Town B. It uses 1 gallon of gas for every 24 miles traveled.
a) How many gallons of gas does the van use if it travels 3x miles?
Answer:
\(\frac{3x}{24}\) gallons of gas
Explanation:
1 gallon = 24 miles
3x miles = \(\frac{3x}{24}\) gallons of gas.
b) The van uses 2y gallons of gas for its journey from Town A to Town B. Find the distance between Town A and Town B.
Answer:
48y miles
Explanation:
1 gallon = 24 miles
2y gallons = 2y x 24 miles
= 48y miles
Question 3.
Brian bought x apples and some oranges. Brian bought 3 more oranges than apples.
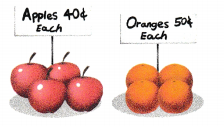
a) Find the total number of fruit Brian bought in terms of x.
Answer:
2x + 3
Explanation:
x apples
x + 3 oranges
the total number of fruit Brian bought in terms of x is
= x + x +3 = 2x + 3
b) Find the total amount of money, in cents, that Brian spent on the fruit. Give your answer in terms of x.
Answer:
80x + 150 cents
Explanation:
2x ( 40 ) + 3 ( 50)
= 80x + 150 cents
c) If Brian could have bought exactly 12 pears with the amount of money that was spent on the apples and oranges, find the cost of each pear, in cents, in terms of x.
Answer:
\(\frac{80x+150}{12}\)
Explanation:
12p = 80x + 150 cents
p = \(\frac{80x+150}{12}\)
Question 4.
A rectangle has a width of x centimeters and a perimeter of 8x centimeters. A square has sides of length \(\frac{1}{4}\) that of the length of the rectangle.
a) Find the length of the rectangle.
Answer: 3x
Explanation:
8x = 2(x + l)
=> 8x/2= x + l
=> 4x = x + l
=> 4x – x = l
length = 3x
b) Find the perimeter of the square.
Answer: 3x
Explanation:
A square has sides of length \(\frac{1}{4}\)
the perimeter of the square = 4 x \(\frac{3x}{4}\) = 3x
c) Find how many centimetres greater the rectangle’s perimeter is than the square’s perimeter if x = 4.
Answer:
20 centimetres greater the rectangle’s perimeter is than the square’s perimeter.
Explanation:
rectangle’s perimeter = 8x
square’s perimeter = 3x
if x = 4.
rectangle’s perimeter = 8x = 8 x 4 = 32 cm
square’s perimeter = 3x = 3 x = 12 cm
32 – 12 = 20 cm
20 centimetres greater the rectangle’s perimeter is than the square’s perimeter
d) Find how many square centimetres greater the rectangle’s area is than the square’s area if x = 4.
Answer:
39 sq cm
Explanation:
Square area = side x side
= \(\frac{3x}{4}\) x \(\frac{3x}{4}\)
= \(\frac{3x}{4}\) x \(\frac{3x}{4}\) substitute x = 4
= \(\frac{3 x 4}{4}\) x \(\frac{3 x 4}{4}\) = 9 sq cm
Rectangle area = length x width
= 3x . x = 3 x 4 . 4 = 48 sq cm
48 – 9 = 39 sq cm many square centimeters greater the rectangle’s area is than the square’s area.
Question 5.
Jose bought 4 comic books and 2 nonfiction books. The 4 comic books cost him 8y dollars. If the cost of one nonfiction book is (3 + 7y) dollars more expensive than the cost of one comic book, find
a) the cost of the 2 nonfiction books in terms of y.
Answer:
(15y + 6)/2
Explanation:
4 comic books = 8y
1 comic book = 8y/4 = y/2
one notification book = y/2 + (3 + 7y) = (15y + 6)/2
b) the total amount that Jose spent on the books if y = 4.
Answer:
$98
Explanation:
8y + 15y + 6
if y = 4
= 8.4 + 15.4 + 6
= 32 + 60 + 6
= 98$
Question 6.
Wyatt has (2x – 1) one-dollar bills and (4x + 2) five-dollar bills. Susan has 3x dollars more than Wyatt.
a) Find the total amount of money that Wyatt has in terms of x.
Answer:
22x – 9
Explanation:
Wyatt has (2x – 1) one-dollar bills and (4x + 2) five-dollar bills
2x-1 + 5(4x + 2)
= 2x – 1 + 20x + 10
= 22x – 9
b) Find the number of pens that Wyatt can buy if each pen costs 50 cents.
Answer:
44x -1 8 pens
Explanation:
Wyatt has (2x – 1) one-dollar bills and (4x + 2) five-dollar bills
2x-1 + 5(4x + 2)
= 2x – 1 + 20x + 10
= 22x – 9/(1/2)
= (22x – 9 ) x 2
= 44x -1 8 pens can buy
c) If x = 21, find how much money Susan will have now if Wyatt gives her half the number of five-dollar bills that he has.
Answer:
516$
Explanation:
Susan has 3x dollars more than Wyatt
Wyatt has 22x – 9
2x – 1 + (5(4x + 2))/2
= (4x – 2 + 20x + 10)/2
= (24x – 8)/2
now Susan has
x = 21
= 2x – 1+(4x + 2)/2 + 3x
= 2x-1 + (4 x 21 +2 )/2 + 3 x 21
= 2×21 -1 + 86/2 + 63
= 41 + 43 + 63
= 147$ (to be re calculated)
Brain @ Work
Question 1.
Find the perimeter of the figure in terms of x, given that all the angles in the figure are right angles. If x = 5.5, evaluate this expression.
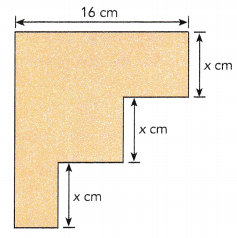
Answer:
65.1 cm
Explanation:
Perimeter of the given figure
= 3x + 16 + 5x + 16 – 2x
= 3 x 5.5 + 16 + 5 x 5.5 + 16 – 2 x 5.5
= 16.5 + 16 + 27.5 + 16 – 11
= 65.1 cm