Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 8 Equations and Inequalities to score better marks in the exam.
Math in Focus Grade 6 Course 1 B Chapter 8 Answer Key Multiplying and Dividing Fractions and Decimals
Math in Focus Grade 6 Chapter 8 Quick Check Answer Key
Complete with =, >, or <.
Question 1.
25 ![]() -26
-26
Answer:
25 > -26,
Explanation:
Given to compare 25 and -26 as 25 is greater than -26 therefore 25 > -26.
Question 2.
12 + 12 + 12 ![]() 3 ∙ 12
3 ∙ 12
Answer:
12 + 12 + 12 = 36,
Explanation:
As 12 + 12 + 12 = 36 and 3 X 12 is 36 so both are equal therefore 12 + 12 + 12 = 36.
Question 3.
40 ÷ 8 ![]() 8 ÷ 40
8 ÷ 40
Answer:
40 ÷ 8 = 8 ÷ 40,
Explanation:
As 40 ÷ 8 is 5 and 8 ÷ 40 is 5 therefore 40 ÷ 8 = 8 ÷ 40.
Question 4.
-16 ![]() -7
-7
Answer:
-16 < -7,
Explanation:
Given to compare between – 16 and – 7 as – 16 is lessthan -7 so -16 < -7.
Write an algebraic expression for each of the following.
Question 5.
The sum of 15 and p
Answer:
x = 15 + p,
Explanation:
An algebraic expression for the sum of 15 and p, let it be x so x = 15 + p.
Question 6.
The difference “q less than 10”
Answer:
x – q < 10,
Explanation:
Given the difference “q less than 10” is let it be x so x – q < 10.
Question 7.
The product of r and 23
Answer:
x = r X 23,
Explanation:
Given the product of r and 23 is let it be x so x = r X 23.
Question 8.
Divide s by 11.
Answer:
x = s ÷ 11,
Explanation:
Given divide s by 11 so let it be x so x = s ÷ 11.
Evaluate each expression for the given values of the variable.
Question 9.
3x + 5 when x = 9 and x = 12
Answer:
3x + 5 = 32, when x = 9,
3x + 5 = 41, when x = 12,
Explanation:
Given to find 3x + 5 when x = 9, so 3 X 9 + 5 = 27 + 5 = 32, when x = 12 we get 3x + 5 = 3 x 12 + 5 = 36 + 5 = 41.
Question 10.
28 – 4x when x = 4 and x = 7
Answer:
28 – 4x = 12, when x = 4,
28 – 4x = 0 when x = 7,
Explanation:
Given when x = 4 the equation 28 – 4x is 28 – 16 = 12, when x = 7 then the equation becomes 28 – 4 X 7 = 28 – 28 = 0.
Plot the points on a coordinate plane.
Question 11.
K (2, 1), L (3, 3), M (0, 6), and N (7, 5)
Answer:
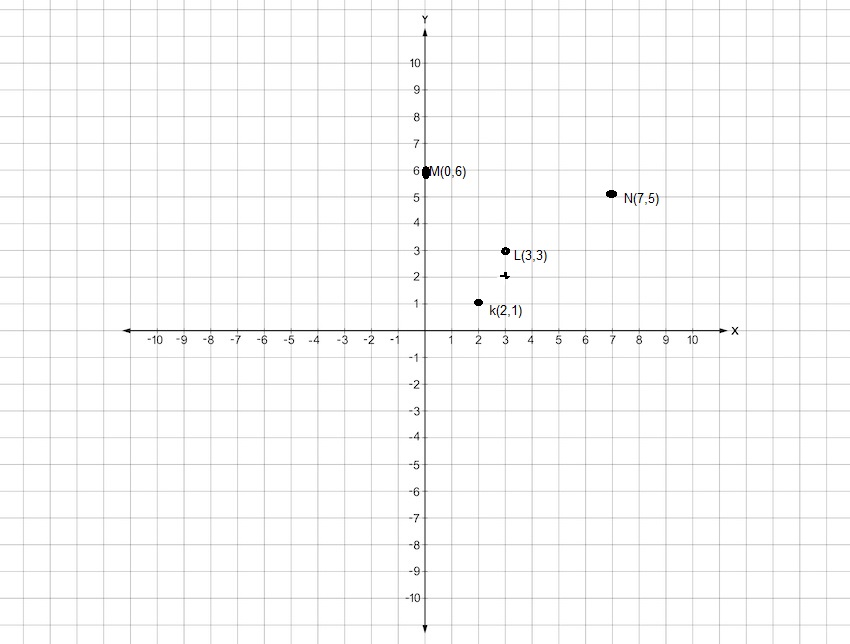
Explanation:
Given to plot the points on a coordinate plane as K (2, 1), L (3, 3), M (0, 6), and N (7, 5) above.