This handy Math in Focus Grade 6 Workbook Answer Key Cumulative Review Chapters 8-11 detailed solutions for the textbook questions.
Math in Focus Grade 6 Course 1 B Cumulative Review Chapters 8-11 Answer Key
Concepts and Skills
Represent the solution set of each Inequality on a number line. (Lesson 8.3)
Question 1.
p ≤ 35
Answer:

Explanation:
Shown p ≤ 35 inequality with red line on the number line above the point starts from 35 and moves towards left side values less than or equal to 35.
Question 2.
q ≥ 12.6
Answer:
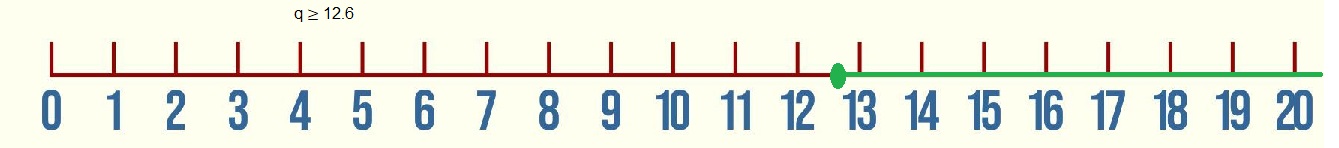
Explanation:
Shown q ≥ 12.6 inequality with green line on the number line above, the points starts from 12.6 on the number lines and moves towards right side greater than or equal to 12.6.
Question 3.
r < \(\frac{4}{5}\)
Answer:

Explanation:
Shown r < \(\frac{4}{5}\) = 0.8 inequality with green line on the number line above the point starts from 0.8 and moves towards left side values less than r < \(\frac{4}{5}\) = 0.8.
Question 4.
s > 13\(\frac{1}{2}\)
Answer:
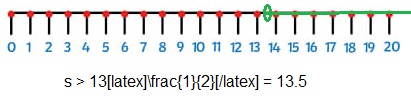
Explanation:
Shown s > 13\(\frac{1}{2}\) = 13.5 inequality with green line on the number line above, the points starts from 13.5 on the number lines and moves towards right side greater than 13.5.
Use graph paper. Plot the points on a coordinate plane and answer the question. (Lesson 9.1)
Question 5.
a) Plot points A (-2, -2) and B (-10, -2) on a coordinate plane. Connect the two points to form a line segment.
Answer:
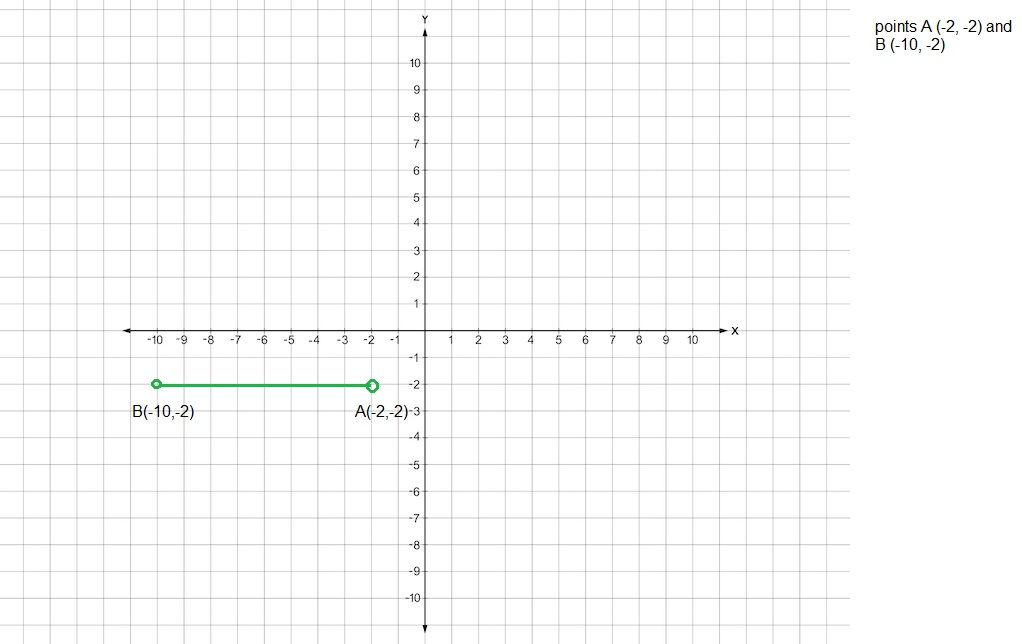 Explanation:
Explanation:
Plotted points A (-2, -2) and B (-10, -2) on a coordinate plane and connected the two points to form a line segment as shown above.
b) Point C lies above \(\overline{A B}\), and is 5 units away from the x-axis. If triangle ABC is an isosceles triangle with base \(\overline{A B}\), find the coordinates of point C.
Answer:
If Point C lies above \(\overline{A B}\), and is 5 units away from the x-axis. If triangle ABC is an isosceles triangle with base \(\overline{A B}\) and points A (-2, -2) and B (-10, -2) as AC = BC, Let Point be (x,y) so Square root of (x-(-2))2 +(y-(-2))2 = square root of (x -(-10))2 + (y-(-2))2 ,
(x + 2)2 + (y + 2)2 = (x + 10)2 + (y + 2)2 ,
4x + 4 = 20x + 100,
16x = 4 – 100 = -96,
x = -96/4 = -24 and y = 0
c) Points D and E lie below \(\overline{A B}\) such that ABDE is a rectangle. If BD is 7 units, find the coordinates of points D and E.
Answer:
Find the area of each figure. (Lesson 10.2)
Question 6.
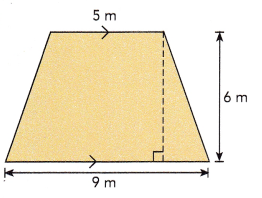
Answer:
The area is 42 square meters,
Explanation:
Given figure is trapezoid and area of trapezoid is \(\frac{1}{2}\)(a +b) X h where a and b are bases of parallel sides so a = 9 m, b = 5 m and h = 6 m, therefore area = \(\frac{1}{2}\)(9 m + 5 m) X 6 m = 7 m X 6 m = 42 square meters.
Question 2.
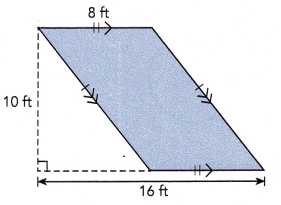
Answer:
The area is 120 square feet,
Explanation:
Given figure is trapezoid and area of trapezoid is \(\frac{1}{2}\)(a +b) X h where a and b are bases of parallel sides so a = 16 ft, b = 8 ft and h = 10 ft, therefore area = \(\frac{1}{2}\)(16 ft + 8 ft) X 10 ft = 12 ft X 10 ft = 120 square feet.
Solve. Show your work. (Lessons 8.2, 11.1, 11.2)
Question 8.
The cost of a shirt is p dollars. The cost of a pair of pants is twice the cost of the shirt. If the cost of the pair of pants is t dollars, express t in terms of p.
Answer:
t = 2p dollars,
Explanation:
Given the cost of a shirt is p dollars. The cost of a pair of pants is twice the cost of the shirt. If the cost of the pair of pants is t dollars, So t in terms of p is t = 2p dollars.
Question 9.
A can has a circular base of diameter 8 centimeters. Find the area of this base. Use 3.14 as an approximation for π.
Answer:
The area of the base is 50.24 square centimeters,
Explanation:
Given A can has a circular base of diameter 8 centimeters. As the area is πr2 where radius = 8 cms/2 = 4 cms, So area = 3.14 X 4 cms X 4 cms = 50.24 square centimeters.
Question 10.
The cross section of a bowl is in the shape of a semicircle. The area of the semicircle is 77 square centimeters. Find its radius. Use \(\frac{22}{7}\) as an approximation for π.
Answer:
Radius is approximately 7 cms,
Explanation:
Given the cross section of a bowl is in the shape of a semicircle. The area of the semicircle is 77 square centimeters.
As area of semicircle is \(\frac{1}{2}\) X πr2 so 77 sq cms = \(\frac{1}{2}\) X 3.14 X r2 ,
r2 = 77 sq cms X 2/3.14 = 154 sq cms/3.14 = 49.04 sq cms, therefore r = square root of 49.04 approximately 7 cms.
Question 11.
The circumference of a platinum ring is 44 millimeters. Find its radius. Use \(\frac{22}{7}\) as an approximation for π.
Answer:
The radius of the platinum ring is 7.006 millimeters,
Explanation:
Given the circumference of a platinum ring is 44 millimeters as circumference is 2πr so r = 44 millimeter/2π, r = 44 mm/6.28 = 7.006 millimeters.
Problem Solving
Solve. Show your work.
Question 12.
Emily weighs x pounds. Jonathan weighs 3 times as much as Emily. If Jonathan weighs 81 pounds, write an equation in terms of x and solve it. (chapter 8)
Answer:
Equation is 3x = 81, Emily weighs 27 pounds,
Explanation:
Given Emily weighs x pounds. Jonathan weighs 3 times as much as Emily. If Jonathan weighs 81 pounds, So equation is 3x = 81 pounds so x = 81/3 = 27 pounds.
Question 13.
Kim has a bag of yo-yos. Some of the yo-yos are red. The rest are yellow. The ratio of the number of red yo-yos to the number of yellow yo-yos is 5 : 9. If Kim has a total of b yo-yos, how many more yellow yo-yos than red yo-yos are there? (Chapter 8)
Answer:
Many more yellow yo-yos than red yo-yos are r = (b -9y)/5,
Explanation:
Given Kim has a bag of yo-yos. Some of the yo-yos are red. The rest are yellow. The ratio of the number of red yo-yos to the number of yellow yo-yos is 5 : 9. If Kim has a total of b yo-yos, let r be red yo-yos and y be yellow yo-yos,
b = 5r + 9y, So many more yellow yo-yos than red yo-yos are r = (b -9y)/5.
Question 14.
The length of a rectangle is 4n centimeters, and it is twice as long as the width. The perimeter of the rectangle is twice as long as that of an equilateral triangle. Find the side length of the triangle in terms of n. (Chapter 10)
Answer:
Side length of the triangle in terms of n is 2n,
Explanation:
Given the length of a rectangle is 4n centimeters and it is twice as long as the width. The perimeter of the rectangle is twice as long as that of an equilateral triangle, length of rectangle = 4n and width is 4n/2 = 2n, So Perimeter p = 2(4n + 2n) = 12n, let a be the side length of the triangle so 12n : 2 = 6n, P = 3a, a = 6n : 3, a = 2n, So Side length of the triangle in terms of n is 2n.
Question 15.
The length of the minute hand of a clock is 6.5 centimeters. How far does the tip of the minute hand travel in an hour? Use 3.14 as an approximation for π. (Chapter 11)
Answer:
The minute hand travel in an hour is 40.82 centimeters,
Explanation:
Given the length of the minute hand of a clock is 6.5 centimeters. The tip of the minute hand travel in an hour is the circumference with radius as 6.5 centimeters, so it is 2π r = 2 X 3.14 X 6.5 centimeters = 40.82 centimeters.
Question 16.
The area of trapezoid ABCE is 36 square meters. Find the height of the trapezoid. (Chapter 10)
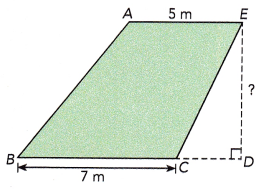
Answer:
The height of the trapezoid is 6 meters,
Explanation:
Area of trapezoid is \(\frac{1}{2}\)(a +b) X h where a and b are bases of parallel sides given a = 7 m, b = 5 m and let height be h m, therefore 36 square meters = \(\frac{1}{2}\)(7 m + 5 m) X h m, height = 2 X 36 sq mts/12 mts = 6 meters.
Find the area of the shaded region. (Chapter 10)
Question 17.
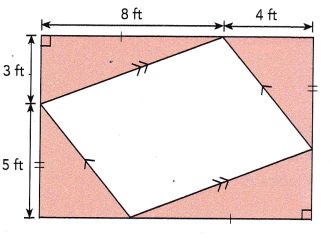
Answer:
The area of the shaded region is 56 square feet,
Explanation:
Given area consists of 2 rectangles one bigger one with length 12 ft and width 8 ft so area is 12 ft X 8 ft = 96 square feet and another small rectangle inside the bigger rectangle with a length 8 ft and width 5 ft so area is 8 ft X 5 ft = 40 square feet now the area of the shaded region is 96 square feet – 40 square feet = 56 square feet.
Question 18.
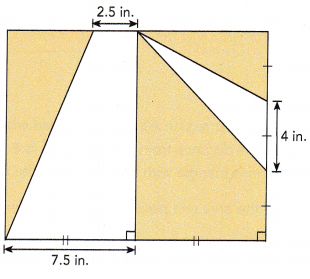
Answer:
The area of the shaded region is 172.5 square inches,
Explanation:
The shape is square inside with 2 non shaded regions are trapezoid and triangle, First area of square with side length 15 in is 15 inches X 15 inches = 225 square inches, Now area of non shaded region first trapezoid we have a as 2.5 inches, b as 7.5 inches, height 7.5 inches, so area is (2.5 inches + 7.5 inches)/2 X 7.5 inches = 37.5 square inches, Area of the non shaded triangle with base 4 inches and height 7.5 inches is 1/2 X 4 inches X 7.5 inches = 15 square inches,
Total area of non shaded region is 37.5 square inches + 15 square inches = 52.5 square inches, Now the area of the shaded region is 225 square inches – 52.5 square inches = 172.5 square inches.
Find the area of the shaded region. Use 3.14 as an approximation for π.
Question 19.
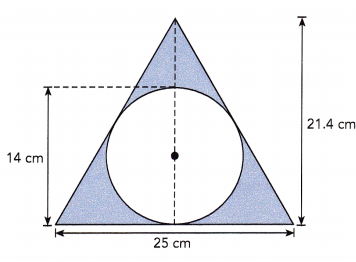
Answer:
The area of the shaded region is 113.64 square centimeters,
Explanation:
The area of the shaded region is area of triangle – area of the circle so first area of the triangle is \(\frac{1}{2}\) X base X height here base is 25 cm and height is 21.4 cm so area is \(\frac{1}{2}\) X 25 cm X 21.4 cm = 267.5 square centimeters, Area of circle is πr2 we have diameter as 14 cm so radius = 14 cm/2 = 7 cm so area is 3.14 X 7 cm X 7 cm = 153.86 sq cms now area of the shaded region is 267.5 sq cms – 153.86 sq cms = 113.64 sq cms.
Question 20.
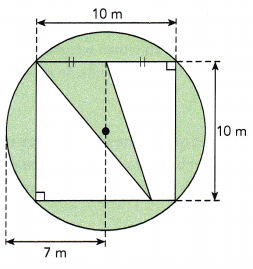
Answer:
The area of the shaded region is 75.11 square meters,
Explanation:
Given a circle and square in it and in square we have 2 small shaded triangles, First the area of the square is 10 m X 10 m = 100 square meters, The area of the circle with radius 7 m is πr2 = 3.14 X 7 m X 7 m = 153.86 square meters,
Area of shaded region without square is 153.86 square meters – 100 square meters = 53.86 square meters, We have 2 triangles shaded regions one traingle area with base side 5 m and height 5 m so its area is 1/2 X 5 m X 5 m = 12.5 square meters another area of square is 1/2 X 5 m X 3.5 m = 8.75 square meters so area of 2 small shaded triangles is 12.5 sq mts + 8.75 sq mts = 21.25 square meters, Now area of the only shaded region is 53.86 square meters + 21.25 square meters = 75.11 square meters.
Solve.
Question 21.
The diagram shows the plan of a square garden. The side length of each grid square is 2 meters. (Chapters 9, 10)
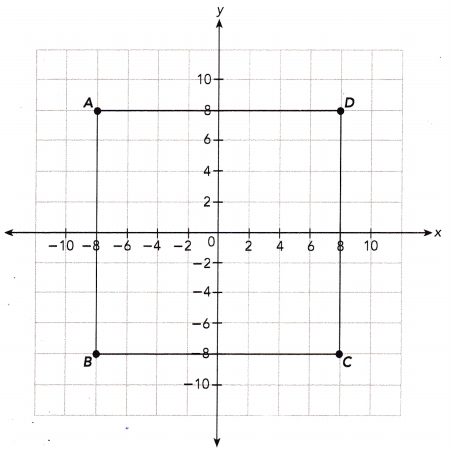
a) A triangular region ABP is surrounded with a wooden fence. The shortest possible distance from point P to \(\overline{A B}\) is 8 meters, and triangle ABP is an isosceles triangle with base \(\overline{A B}\). Find the coordinates of point P.
Answer:
We have A(-8,8) and B(-8,-8) and triangle ABP is an isosceles triangle with base AB means AP = BP,
Square root of (x – (-8))2 + (y – 8)2 = Square root of (x – (-8))2 + (y -(-8))2 ,
-16y + 64 = 16y + 64,
32y = 0,
b) Find the area and perimeter of the garden.
Answer:
Area is 64 square meters, Perimeter of the garden is 32 meters,
Explanation:
Given the plan of a square garden with 8 mts length so area is 8 mts X 8 mts = 64 square meters and perimeter of the garden is 4 X 8 meters = 32 meters.
c) Find the area of the garden that lies outside triangle ASP in square meters.
Answer:
Solve. Use graph paper to answer the question.
Question 22.
An aspen tree is 300 centimeters tall. It grows 15 centimeters taller each month. The height of the tree, h centimeters, over t months is given by h = 300 + 15t. Copy and complete the table, Graph the relationship between t and h. Use 1 unit on the horizontal axis to represent 1 month and 1 unit on the vertical axis to represent 15 centimeters. Start your vertical axis at 300 centimeters. (Chapters 8, 9)
a)

Answer:

Explanation:
Updated the given table as shown above.
b) What is the height of the tree after 3 months?
Answer:
The height of the tree after 3 months is 345 centimeters,
Explanation:
If an aspen tree is 300 centimeters tall. It grows 15 centimeters taller each month. So after 3 months it will grow
300 centimeters + 15 centimeters + 15 centimeters + 15 centimeters = 345 centimeters.
c) Assuming the growth of the tree is constant for the next year, what is the height of the tree after 10 months?
Answer:
The height of the tree after 10 months is 450 centimeters,
Explanation:
Assuming the growth of the tree is constant for the next year, So the height of the tree after 10 months will be 300 centimeters + 10 X 15 centimeters = 300 centimeters + 150 centimeters = 450 centimeters.
d) If the tree is at least 360 centimeters tall, how many months have passed? Express your answer in the form of an inequality in terms of t, where t stands for the number of months that have passed.
Answer:
360 = 300 + 15t,
Explanation:
Given if the tree is at least 360 centimeters tall, how many months have passed so expressing my answer in the form of an inequality in terms of t, where t stands for the number of months that have passed is 360 = 300 + 15t.
e) Name the dependent and independent variables.
Answer:
Dependent is time and height and independent is 15 centimeters taller each month,
Explanation:
Given an aspen tree is 300 centimeters tall. It grows 15 centimeters taller each month. The height of the tree, h centimeters, over t months is given by h = 300 + 15t. Here dependent is time and height and independent is 15 centimeters taller each month.
Solve. Show your work.
Question 23.
A circular garden is surrounded by a cement path that is 1.5 meters wide. Find the area of the path. Use 3.14 as an approximation for n. (Chapter 11)
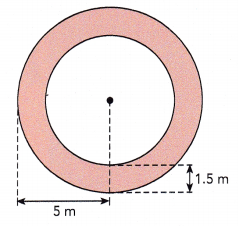
Answer:
The area of the path 40.035 square meters,
Explanation:
Given the radius of the circle with circular path is 5 m so its area is πr2 = 3.14 X 5 m X 5 m = 78.5 square meter, now area of the circle without the path as radius is 5 m – 1.5 m = 3.5 m is 3.14 X 3.5 m X 3.5 m = 38.465 square meter, Now the area of the path only is 78.5 square meter – 38.465 square meter = 40.035 square meter.
Question 24.
Figure PRSV is a parallelogram. The length of \(\overline{V U}\) and \(\overline{U T}\) are equal, The area of parallelogram QRSW is 30 square inches. The length of \(\overline{R S}\) is 6 inches. (Chapter 10)
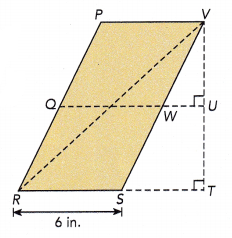
a) Find the height of parallelogram QRSW.
Answer:
The height of parallelogram QRSW is 5 inches,
Explanation:
Given the area of parallelogram QRSW is 30 square inches. The length of \(\overline{R S}\) is 6 inches.
As area of parallelogram is base X height we have base as 6 in. so height of the parallelogram QRSW is 30 square inches/6 inches = 5 inches.
b) Find the area of triangle PRV.
Answer:
The area of triangle PRV is 30 square inches,
Explanation:
As given the length of \(\overline{V U}\) and \(\overline{U T}\) are equal, So length of \(\overline{V U}\) = 5 inches so \(\overline{U T}\) = 5 inches the total length of VT is length of \(\overline{V U}\) + length of \(\overline{U T}\) = 5 inches + 5 inches = 10 inches and PR = VT = 10 inches, PV = RS = 6 inches so the area of triangle PRV is 1/2 X RS X PR = 1/2 X 6 inches X 10 inches = 30 square inches.
c) If you did not know the length of \(\overline{R S}\), explain how you could find the area of triangle PRV.
Answer:
Through Parallelogram,
Explanation:
As we know the area of a triangle is half the product of any of its sides and the corresponding altitude. If a triangle and a parallelogram are on the same base and between the same parallels, then the area of the triangle is equal to half of the area of the parallelogram.