This handy Math in Focus Grade 6 Workbook Answer Key Chapter 11 Review Test detailed solutions for the textbook questions.
Math in Focus Grade 6 Course 1 B Chapter 11 Review Test Answer Key
Chapter Review/Test
Concepts and Skills
Find the circumference and area of each circle. Use \(\frac{22}{7}\) as an approximation for π.
Question 1.
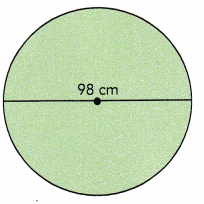
Answer:
Circumfrence: 307.72 cm,
Area: 7,539.14 square centimeters,
Explanation:
Given diameter of the circle as 98 cm so radius is 98 cm/2 = 49 cm, Circumfrence is 2πr = 2 X 3.14 X 49 cm = 307.72 cm, Area of the circle is πr2 = 3.14 X 49 cm X 49 cm = 7,539.14 square centimeters.
Question 2.
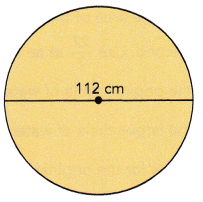
Answer:
Circumfrence: 351.68 cm,
Area: 9,847.04 square centimeters,
Explanation:
Given diameter of the circle as 98 cm so radius is 112 cm/2 = 56 cm, Circumfrence is 2πr = 2 X 3.14 X 56 cm = 351.68 cm, Area of the circle is πr2 = 3.14 X 56 cm X 56 cm = 9,847.04 square centimeters.
Find the distance around each semicircle. Use \(\frac{22}{7}\) as an approximation for π.
Question 3.
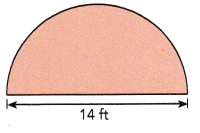
Answer:
The distance around the semicircle is 21.98 ft,
Explanation:
Given diameter of the circle as 14 ft so radius is 14 ft/2 = 7ft, Distance around the semicircle is \(\frac{1}{2}\) X 2πr = 3.14 X 7 ft = 21.98 ft.
Question 4.
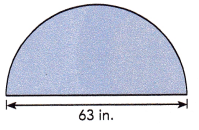
Answer:
The distance around the semicircle is 98.91 in,
Explanation:
Given diameter of the circle as 63 in so radius is 63 in/2 = 31.5 in, Distance around the semicircle is \(\frac{1}{2}\) X 2πr = 3.14 X 31.5 in = 98.91 in.
Find the distance around each quadrant. Round your answer to the nearest tenth. Use 3.14 as an approximation for π.
Question 5.
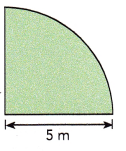
Answer:
The distance around the quadrant is 7.85 m,
Explanation:
Given radius of the circle is 5 m, Distance around the quadrant is \(\frac{1}{4}\) X 2πr = \(\frac{1}{2}\) X πr = \(\frac{1}{2}\) X 3.14 X 5 m = 7.85 m.
Question 6.
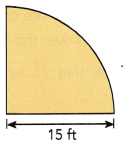
Answer:
The distance around the quadrant is 23.55 ft,
Explanation:
Given radius of the circle is 15 ft, Distance around the quadrant is \(\frac{1}{4}\) X 2πr = \(\frac{1}{2}\) X πr = \(\frac{1}{2}\) X 3.14 X 15 ft = 23.55 ft.
Solve. Show your work.
Question 7.
The diameter of a flying disc is 10 inches. Find the circumference and area of the disc. Use 3.14 as an approximation for π.
Answer:
Circumfrence of the flying disc is 31 inches and area of the flying disc is 78.5 square inches,
Explanation:
Given diameter of the flying disc as 10 inches so radius is 10 in/2 = 5 in, Circumfrence is 2πr = 2 X 3.14 X 5 in = 31.4 in, Area of the circle is πr2 = 3.14 X 5 in X 5 in = 78.5 square inches.
Question 8.
The area of a compact disc is 452\(\frac{4}{7}\) square centimeters. What is the diameter of the compact disc? Use \(\frac{22}{7}\) as an approximation for π.
Answer:
The diameter of the compact disc is 26.22 centimeters,
Explanation:
Given the area of a compact disc is 452\(\frac{4}{7}\) square centimeters. Let d be the diameter of the compact disc so 452\(\frac{4}{7}\) square centimeters = πr2 = π X (d/2)2 ,
3.14 X d2 = 4 X 452\(\frac{4}{7}\) square centimeters,
d2 = 4 X 3,168 sq cms/7 X 3.14,
d2 = 12,672 sq cms /21.98 = 576.524 therefore d = square root of 576.524 sq cms = 26.22 centimeters.
Question 9.
The circumference of a circular table is 816.4 centimeters. Find the radius of the table. Use 3.14 as an approximation for π.
Answer:
The radius of the table is 130 cntimeters,
Explanation:
Given the circumference of a circular table is 816.4 centimeters means it is 2πr, So radius = 816.4 cms/2 X 3.14= 816.4 cms/6.28 = 130 centimeters
Problem Solving
Solve. Show your work.
Question 10.
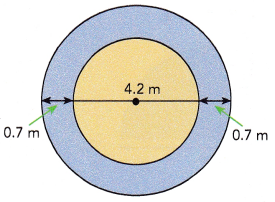
A water fountain shoots up a jet of water. The water falls back down onto the ground in the shape of a circle. Michelle wants the circle of water on the ground to be 0.7 meter wider on each side. She gradually increases the strength of the water jet. The area of the circle of water increases at 0.2 square meter per second. Use \(\frac{22}{7}\) as an approximation for n.
a) Find the area of the original circle of water.
Answer:
The area of the original circle of water is 13.8474 square meters,
Explanation:
The radius of the original circle of water as diameter 4.2 m is 4.2 m/2 = 2.1 m, So area is 3.14 X 2.1 m X 2.1 m = 13.8474 square meters.
b) Find the area of the larger circle of water.
Answer:
The area of the larger circle of water is 24.6176 square meters,
Explanation:
The radius of the original circle of water as diameter 4.2 m + 0.7 m + 0.7 m = 5.6 m is 5.6 m/2 = 2.8 m, So area is 2 X 3.14 X 2.8 m X 2.8 m = 24.6176 square meters.
c) How long does it take for the original circle of water to become the larger circle of water? Round your answer to the nearest second.
Answer:
It take for the original circle of water to become the larger circle of water to the nearest second is 54 seconds,
Explanation:
The area increased from the orignal circle to larger circle is 24.6176 square meters – 13.8474 square meters = 10.7702 square meters, if the area of the circle of water increases at 0.2 square meter per second long does it take for the original circle of water to become the larger circle of water is 10.7702/ 0.2 = 53.851 seconds nearest second is 54 seconds.
Question 11.
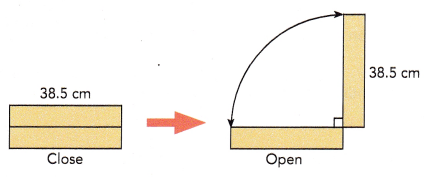
A machine in an assembly line stamps pieces of metal. The stamping plate on the machine travels in a path shaped like the arc of a quadrant as the stamping plate opens and closes. It takes the machine 5 seconds to open and close the stamping plate one time. Use \(\frac{22}{7}\) as an approximation for π.
a) Find the total distance the outside edge of the stamping plate travels when the machine opens and closes one time.
Answer:
The total distance the outside edge of the stamping plate travels when the machine opens and closes one time is 60.442 cms,
Explanation:
Given a machine in an assembly line stamps pieces of metal. The stamping plate on the machine travels in a path shaped like the arc of a quadrant as the stamping plate opens and closes, So the total distance the outside edge of the stamping plate travels when the machine opens and closes one time is distance around the quadrant is \(\frac{1}{4}\) X 2πr we have radius as 38.5 cm so the distance is \(\frac{1}{4}\) X 2 X 3.14 X 38.5 cm = 60.445 cms.
b) Find the speed of the stamping plate’s outside edge in centimeters per second.
Answer:
The speed of the stamping plate’s outside edge in centimeters per second is 12.089 centimeters per second,
Explanation:
Given it takes the machine 5 seconds to open and close the stamping plate one time, So the speed of the stamping plate’s outside edge in centimeters per second is 60.445 cms/5 seconds = 12.089 centimeters per second.
c) Assume the machine starts and ends in an open position. How many seconds will it take the machine to stamp 500 pieces of metal?
Answer:
Answer:
Seconds will it take the machine to stamp 500 pieces of metal is 6,044.5 seconds,
Explanation:
Assuming the machine starts and ends in an open position. So seconds will it take the machine to stamp 500 pieces of metal is 12.089 centimeters per second X 500 = 6,044.5 seconds.
Question 12.
The figure shows four identical quadrants enclosed in a square. The side length of the square is 20 inches. Find the area of the blue part. Use 3.14 as an approximation for π.
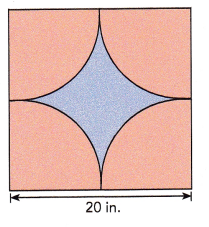
Answer:
The area of the blue part is 321.5 square inches,
Explanation:
The figure shows four identical quadrants enclosed in a square. The side length of the square is 20 inches, The area of the squar is 20 in X 20 in = 400 sq in. As diameter is 20 in radius is 20 in/2 = 10 in so area of four quadrants is \(\frac{1}{4}\) X πr2 = \(\frac{1}{4}\) X 3.14 X 10 in X 10 in = 78.5 square inches. Now area of the blue part is 400 square inches – 78.5 square inches = 321.5 square inches.
Question 13.
The figure shows 3 identical circles. X, Y, and Z are the centers of the circles, and the radius of each circle is 15 feet. \(\frac{1}{6}\) of each circle is shaded. What is the total area of the shaded portion? Round your answer to the nearest tenth of a foot. Use 3.14 as an approximation for π.
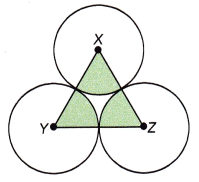
Answer:
The total area of the shaded portion is 350 square feet,
Explanation:
Given the figure shows 3 identical circles. X, Y, and Z are the centers of the circles, and the radius of each circle is 15 feet. \(\frac{1}{6}\) of each circle is shaded. So the total area of the shaded portion first we calculate area of the circle with radius 15 feet is πr2 = 3.14 X 15 feet X 15 feet = 706.5 square feet so the area of shaded circle is \(\frac{1}{6}\) X 706.5 square feet = 117.75 square feet so we have 3 identical circles shaded so its total area is 3 X 117.75 square feet is 353.25 nearest to 350 square feet.
Question 14.
The figure is made up of one semicircle and two quadrants. The distance around the figure is 97.29 inches. Find the value of k. Use 3.14 as an approximation for π.
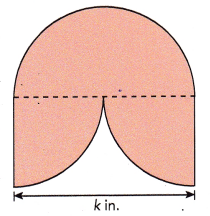
Answer:
The value of k is 15.492 inches,
Explanation:
Given the figure is made up of one semicircle and two quadrants. The distance around the figure is 97.29 inches and the diameter is k in. first the distance of semi circle is \(\frac{1}{2}\) X 2πr = 3.14 X k in. = 3.14k in. Now the area of 2 quadrants is 2 X \(\frac{1}{4}\) X 2πr =3.14k in. Given the distance of fiqure as 97.29 inches = 3.14k inches + 3.14 k inches = 6.28k inches, Therefore k = 97.29/6.28 = 15.492 inches.