Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 8 Review Test to score better marks in the exam.
Math in Focus Grade 6 Course 1 B Chapter 8 Review Test Answer Key
Concepts and Skills
Solve each equation using the concept of balancing. Write all fraction answers in simplest form.
Question 1.
x + 8 = 27
Answer:
x = 19,
Explanation:
Given x + 8 = 27, So x = 27 – 8 = 19.
Question 2.
\(\frac{10}{11}\) = a + \(\frac{4}{11}\)
Answer:
a=\(\frac{6}{11}\),
Explanation:
Given \(\frac{10}{11}\) = a + \(\frac{4}{11}\), So a = \(\frac{10}{11}\) – \(\frac{4}{11}\) both have denominators common so we subtract only numerators so we get a = \(\frac{10 – 4}{11}\) = \(\frac{6}{11}\).
Question 3.
f + 3.8 = 9.2
Answer:
f = 5.4,
Explanation:
Given f + 3.8 = 9.2, So f = 9.2 – 3.8 = 5.4.
Question 4.
42 = y – 14
Answer:
y = 56,
Explanation:
Given 42 = y – 14, y = 42 + 14 = 56.
Question 5.
k – \(\frac{7}{8}\) = 2\(\frac{11}{24}\)
Answer:
k = 3\(\frac{1}{3}\)[/latex]
Explanation:
Given k – \(\frac{7}{8}\) = 2\(\frac{11}{24}\), k = 2\(\frac{11}{24}\) + \(\frac{7}{8}\) = \(\frac{59}{24}\) + \(\frac{7}{8}\) as denominators are different first we make them same
so we multiply \(\frac{7}{8}\) numerator and denominator by 3 as \(\frac{7 X 3}{8 X 3}\) = \(\frac{21}{24}\) now both denominators are same we add numerators \(\frac{59 + 21}{24}\) = \(\frac{80}{24}\) both have common factors so \(\frac{8 X 10}{8 X 3}\) we get \(\frac{10}{3}\) as numerator is greater than denominator we can further write as mixed fraction as \(\frac{3 X 3 + 1}{3} = 3[latex]\frac{1}{3}\)[/latex].
Question 6.
n – 2.7 = 13.4
Answer:
n = 16.1,
Explanation:
Given n- 2.7 = 13.4, So n = 13.4 + 2.7 = 16.1.
Question 7.
6h = 84
Answer:
h = 14,
Explanation:
Given 6h = 84, So h = 84/6,
6)84(14
60
24
24
0
So h = 14.
Question 8.
75.6 = 7.2r
Answer:
r = 10.5,
Explanation:
Given 75.6 = 7.2r, So r = 75.6/7.2,
7.2)75.6(10.5
72
3.6
3.6
0
So r = 10.5.
Question 9.
\(\frac{4}{5}\)p = 10
Answer:
p = 12.5,
Explanation:
Given \(\frac{4}{5}\)p = 10, p = 10/\(\frac{4}{5}\), p= \(\frac{10 X 5}{4}\) = \(\frac{50}{4}\) =
4)50(12.5
40
10
8
20
20
0
So p = 12.5.
Question 10.
9 ∙ \(\frac{3}{5}\) = \(\frac{8}{11}\)w
Answer:
w = 13\(\frac{8}{40}\),
Explanation:
Given 9 ∙ \(\frac{3}{5}\) = \(\frac{8}{11}\)w, w = \(\frac{9 X 5 + 3}{5}\) X \(\frac{11}{8}\) = \(\frac{48 X 11}{5 X 8}\) = \(\frac{528}{40}\) as numerator is greater than denominator so we write in mixed fraction \(\frac{40 X 13 + 8}{40}\) = 13\(\frac{8}{40}\).
Represent the solution set of each inequality on a number line.
Question 11.
b < 7
Answer:
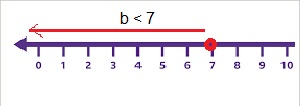
Explanation:
Given to show b < 7 inequality on a number line as b is less than 7 so it starts at 7 and red line moves towards the left side on the number line as shown above.
Question 12.
b > 13
Answer:

Explanation:
Given to show b > 13 inequality on a number line as b is greater than 13 so it starts at 13 and red line moves towards the right side on the number line as shown above.
Question 13.
m ≥ 24
Answer:

Explanation:
Given to show m ≥ 24 inequality on a number line as m is greater than or equal to 24 so it starts at 24 and red line moves towards the right side on the number line as shown above.
Question 14.
m ≤ 38
Answer:

Explanation:
Given to show m ≤ 38 inequality on a number line as m is less than or equal to 38 so it starts at 38 and red line moves towards the left side on the number line as shown above.
Question 15.
g > \(\frac{2}{3}\)
Answer:
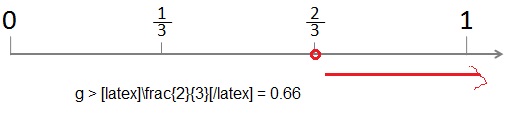
Explanation:
Given to show g > \(\frac{2}{3}\) = 0.666 inequality on a number line as g is greater than 0.66 so it starts at 0.66 and red line moves towards the right side on the number line as shown above.
Question 16.
g ≤ 5\(\frac{3}{5}\)
Answer:
Explanation:
Given to show g ≤ 5\(\frac{3}{5}\) = \(\frac{5 X 5 + 3}{5}\) = \(\frac{28}{5}\) = 5.6 inequality on a number line as g is less than or equal to 5.6 so it starts at 5.6 and red line moves towards the left side on the number line as shown above.
Question 17.
z < 7.1
Answer:

Explanation:
Given to show z < 7.1 inequality on a number line as z is less than 7.1 so it starts at 7.1 and red line moves towards the left side on the number line as shown above.
Question 18.
z ≥ 10.4
Answer:

Explanation:
Given to show z ≥ 10.4 inequality on a number line as m is greater than or equal to 10.4 so it starts at 10.4 and red line moves towards the right side on the number line as shown above.
Write an inequality for each number line.
Question 19.

Answer:
x ≥ 9,
Explanation:
As seen on the number line let us take the point as x it starts exactly at 9 and moves towards right side means it is greater so the inequality is x ≥ 9.
Question 20.

Answer:
x < 16,
Explanation:
As seen on the number line let us take the point as x it starts from 16 and moves towards left side means lesser so the inequality is x <16.
Question 21.
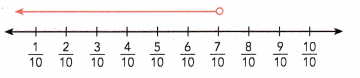
Answer:
x < \(\frac{7}{10}\),
Explanation:
As seen on the number line let us take the point as x it starts from \(\frac{7}{10}\) and moves towards left side means lesser so the inequality is x < \(\frac{7}{10}\).
Question 22.

Answer:
x ≥ 12.5,
Explanation:
As seen on the number line let us take the point as x it starts exactly at 12.5 and moves towards right side means it is greater so the inequality is x ≥ 12.5.