Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 10 Lesson 10.3 Area of Other Polygons to score better marks in the exam.
Math in Focus Grade 6 Course 1 B Chapter 10 Lesson 10.3 Answer Key Area of Other Polygons
Math in Focus Grade 6 Chapter 10 Lesson 10.3 Guided Practice Answer Key
Give the minimum number of identical triangles you could divide each regular polygon into so that you could find the area of the polygon.
Question 1.
Answer:
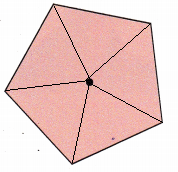
Draw lines from the center of the pentagon, leading to each vertex corner. 5 such lines can be drawn. Thus, 5 identical triangles can be drawn for the given figure.
Area of polygon = n×Area of triangle
Where ‘n’ is the number of sides.
Area of triangle = \(\frac{1}{2}\)×b×h
Area of polygon = n×\(\frac{1}{2}\)×b×h
Here n equals 5
Area of polygon = 5×\(\frac{1}{2}\)×b×h
Question 2.
Answer:
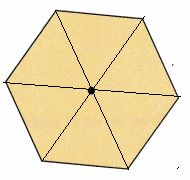
Draw lines from the center of the pentagon, leading to each vertex corner. 6 such lines can be drawn. Thus, 6 identical triangles can be drawn for the given figure.
Area of polygon = n×Area of triangle
Where ‘n’ is the number of sides.
Area of triangle = \(\frac{1}{2}\)×b×h
Area of polygon = n×\(\frac{1}{2}\)×b×h
Here n equals 6
Area of polygon = 6×\(\frac{1}{2}\)×b×h
Count the number of sides in each figure.
Complete.
Question 3.
Blake drew a regular pentagon with side lengths of 6 inches. He divided the pentagon into 5 identical triangles, and measured the height of one of the triangles to be 4.1 inches. Find the area of the pentagon.
Area of triangle = \(\frac{1}{2}\)bh
= ![]() •
• ![]() •
• ![]()
= ![]() im.2
im.2
Area of pentagon = ![]() • area of triangle
• area of triangle
= ![]() •
• ![]()
= ![]() in.2
in.2
The area of the pentagon is ![]() square inches.
square inches.
Answer:
Given that a regular pentagon is divided into 5 identical triangles with side lengths of 6 inches. The height of one of the triangles to be 4.1 inches.
Therefore, the base will measure 6 in and the height will measure 4.1 in.
Area of triangle = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×6×4.1
= 24.6 ÷ 2
= 12.3 sq.in
There are 5 such identical triangles.
Area of pentagon = 5×area of triangle
= 5×12.3
= 61.5 sq.in
The area of the pentagon is 61.5 sq.in
Question 4.
Melanie drew a regular hexagon with side lengths of 28 centimeters. She divided the hexagon into 6 identical triangles and measured the height of one of the triangles to be 24.2 centimeters. Find the area of the hexagon.
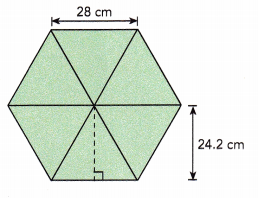
Area of triangle = \(\frac{1}{2}\)bh
= ![]() •
• ![]() •
• ![]()
= ![]() cm2
cm2
Area of hexagon = ![]() • area of triangle
• area of triangle
= ![]() •
• ![]()
= ![]() cm2
cm2
The area of the hexagon is ![]() square centimeters.
square centimeters.
Answer:
Given that a regular hexagon is divided into 6 identical triangles with side lengths of 28 cm. The height of one of the triangles to be 24.2cm.
Area of triangle = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×28×24.2
= \(\frac{1}{2}\)×677.6
= 338.8 sq.cm
There are 6 such identical triangles.
Area of hexagon = 6×area of triangle
= 6 × 338.8
= 2032.8 sq.cm
The area of the hexagon is 2032.8 sq.cm
Math in Focus Course 1B Practice 10.3 Answer Key
Give the minimum number of identical triangles you could divide each regular polygon into so that you could find the area of the polygon.
Question 1.
Answer:
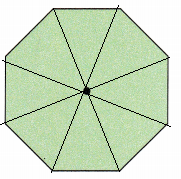
Explanation:
Draw lines from the center of the pentagon, leading to each vertex corner. 8 such lines can be drawn. Thus, 8 identical triangles can be drawn for the given figure.
Area of polygon = n×Area of triangle
Where ‘n’ is the number of sides.
Area of triangle = \(\frac{1}{2}\)×b×h
Area of polygon = n×\(\frac{1}{2}\)×b×h
Here n equals 8
Area of polygon = 8×\(\frac{1}{2}\)×b×h
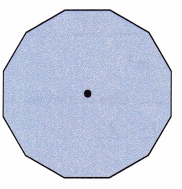
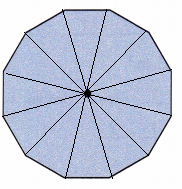
Question 2.
Answer:
Explanation:
Draw lines from the center of the pentagon, leading to each vertex corner. 12 such lines can be drawn. Thus, 12 identical triangles can be drawn for the given figure.
Area of polygon = n×Area of triangle
Where ‘n’ is the number of sides.
Area of triangle = \(\frac{1}{2}\)×b×h
Area of polygon = n×\(\frac{1}{2}\)×b×h
Here n equals 12
Area of polygon = 12×\(\frac{1}{2}\)×b×h
Solve.
Question 3.
Derrick drew a regular pentagon with side lengths of 8 centimeters. He divided the pentagon into 5 identical triangles, and measured the height of one of the triangles to be 5.5 centimeters. Find the area of the pentagon.
Answer:
Given that a regular pentagon is divided into 5 identical triangles with side lengths of 8 cm. The height of one of the triangles is 5.5 cm.
Therefore, the base will be of length 8cm and the height will be 5.5cm.
Area of triangle = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×8×5.5
= 44÷ 2
= 22 sq.cm
There are 5 such identical triangles.
Area of pentagon = 5×area of triangle
= 5×22
= 110 sq.cm
The area of the pentagon is 110 sq.cm
Question 4.
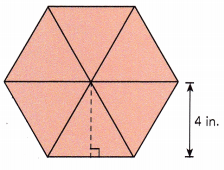
Lydia drew a regular hexagon. She divided it into 6 identical triangles, and measured the height of one of the triangles to be 4 inches. The area of the hexagon is 55.2 square inches. Find the length of each side of the hexagon.
Answer:
Given that a regular hexagon is divided into 6 identical triangles. The height of one of the triangles is 4 in and the area of hexagon is 55.2 sq.in
Let us assume the side length as ‘b’.
Area of triangle = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×b×4
= 2×b
There are 6 such identical triangles.
Area of hexagon = 6×area of triangle
55.2 = 6×2×b
55.2 = 12×b
55.2÷12 = 12×b÷12
4.6 = b
Thus, the length of each side of the hexagon will be 4.6 in
Question 5.
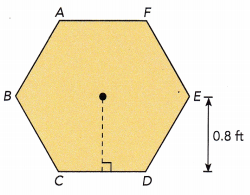
A floor tile is in the shape of a regular hexagon. Greg uses 187.5 floor tiles for a room. The area of the room is 450 square feet. Find the length of each side of the hexagon.
Answer:
Given that 187.5 floor tiles of a regular hexagon shape are used for a room. The area of the room is 450 sq.ft and height of one of triangles is 0.8 ft.
Number of hexagons used = 187.5
Total area = 450 sq.ft
Height of a triangle = 0.8 ft
Area of room = n×Area of trinagle
Area of room = n×\(\frac{1}{2}\)×b×h, here n = 187.5
450 = 187.5×b×0.8
450 = 150×b
450÷150 = 150×b÷150
3 = b
Thus, the length of each side of the hexagon will be 3 ft.
Use the given information to find the area of each regular polygon.
Question 6.
The shaded area is 9.7 square inches.
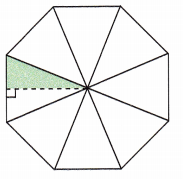
Answer:
Given that the area of shaded region is 9.7 sq.in
Given figure has 8 identical triangles. One of the triangle is divided into two equal triangles and one part of them is shaded.
Therefore, the area of one trinangle will be 9.7+9.7 = 19.4 sq.in
There are 8 such triangles in the given polygon.
Area of polygon = 8×area of triangle
= 8×19.4
= 155.2 sq.in
Question 7.
The shaded area is 12.8 square centimeters.
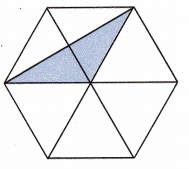
Answer:
Given figure has 6 identical triangles. By observing the polygon, the shaded region is half of the two triangles.
Area of two triangles will be 12.8+12.8 = 25.6 sq.cm
Since we have area of 2 traingles and there are such 6 triangles.
Area of polygon will be 3×Area of two triangles
= 3 × 25.6
= 76.8 sq.cm
Question 8.
Suppose you have three identical equilateral triangles. Use a sketch to show how you can make each of the following from two or more of the triangles. Identify the quadrilateral.
a) a quadrilateral whose area is two times as great as an equilateral triangle.
Answer:
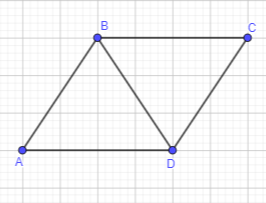
Explanation:
Two identical equilateral triangles are taken to form a quadrilateral whose area is two times as great as an equilateral triangle.
As shown in the figure, the formed quadrilateral from two equilateral traingles is a parallelogram.
b) a quadrilateral whose area is three times as great as an equilateral triangle.
Answer:
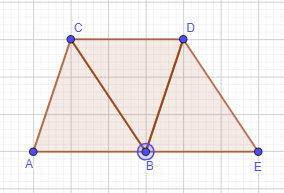
Explanation:
Three identical equilateral triangles are taken to form a quadrilateral whose area is three times as great as an equilateral triangle.
As shown in the figure, the formed quadrilateral from three equilateral traingles is a trapezium.
Each figure is made from a regular polygon surrounded by identical triangles. Find the area of each figure.
Question 9.
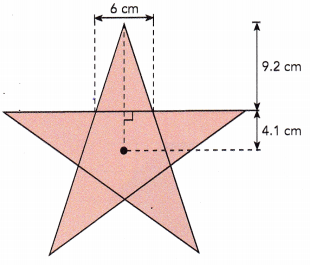
Answer:
The regular polygon in the figure has 5 identical traingles and a pentagon.
The outer triangle measures 9.2 cm high and the base length measures 6 cm.
Area of outer triangles = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×6×9.2
= 55.2÷2
= 27.6 sq.cm
There are 5 triangles, therefore the area of triangles will be 5×area of triangles
= 5×27.6
= 138 sq.cm
Area of pentagon:
A regular pentagon is formed from 5 identical triangles. These traingles are 4.1cm high and base length is 6cm.
Area of inner triangles = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×6×4.1
= \(\frac{1}{2}\)×24.6
= 24.6÷2
= 12.3 sq.cm
Area of pentagon = 5×area of inner triangles
= 5×12.3
= 61.5 sq.cm
Area of polygon = Area of 5 outer triangle + Area of 5 inner triangles
= 138 + 61.5
= 199.5 sq.cm
Question 10.
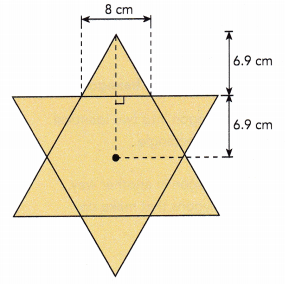
Answer:
The regular polygon in the figure has 6 identical traingles and a hexagon.
The outer triangle measures 6.9 cm high and the base length measures 8 cm.
Area of outer triangles = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×8×6.9
= 55.2÷2
= 27.6 sq.cm
There are 6 such identical traingles.
Area of 6 outer triangles = 6×Area of outer triangles
= 6×27.6
= 165.6 sq.cm
Since the measurements for inner and outer traingle are same, the areas will also be same.
Area of hexagon:
A regular hexagon is formed from 6 identical triangles. These traingles are 6.9cm high and base length is 8cm.
Area of inner triangles = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×8×6.9
= 55.2÷2
= 27.6 sq.cm
Area of 6 inner traingles = 6×Area of outer triangles
= 6×27.6
= 165.6 sq.cm
Area of polygon = Area of 6 outer triangle + Area of 6 inner triangles
= 165.6+165.6
= 331.2 sq.cm