This handy Math in Focus Grade 8 Workbook Answer Key Chapter 11 Lesson 11.4 Dependent Events detailed solutions for the textbook questions.
Math in Focus Grade 8 Course 3 B Chapter 11 Lesson 11.4 Answer Key Dependent Events
Math in Focus Grade 8 Chapter 11 Lesson 11.4 Guided Practice Answer Key
Solve. Show your work.
Question 1.
A deck of four cards with the letters D, E, E, D are placed facing down on a table. Two cards are turned at random to show the letter. Draw a tree diagram to represent the possible outcomes in this compound event.

Let D represent letter D and E represent letter E.
1st draw
P(D) = \(\frac{2}{4}\)
P(E) = \(\frac{2}{4}\)
2nd draw
P(D after D)4 = \(\frac{?}{?}\) There is ![]() D left after 1 D is drawn.
D left after 1 D is drawn.
P(E after D) = \(\frac{?}{?}\) There are ![]() E still after 1 D is drawn.
E still after 1 D is drawn.
P(D after E) = \(\frac{?}{?}\) There are ![]() D still after 1 E is drawn.
D still after 1 E is drawn.
P(E after E) = \(\frac{?}{?}\) There is ![]() E left after 1 E is drawn.
E left after 1 E is drawn.
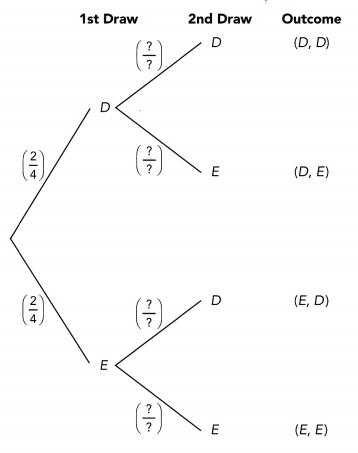
Answer:
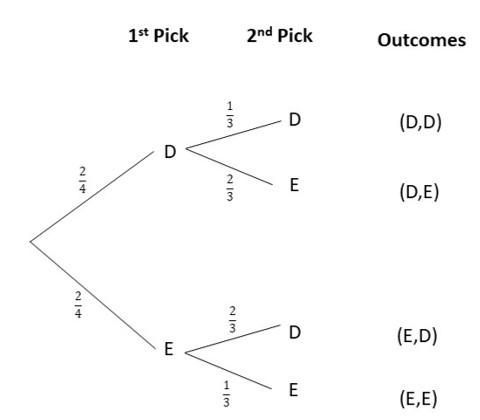
P(D after D)4 = There is 1/3 D left after 1 D is drawn.
P(E after D) = There are 2/3 E still after 1 D is drawn.
P(D after E) = There are 2/3 D still after 1 E is drawn.
P(E after E) = There is 1/3 E left after 1 E is drawn
Question 2.
There are 16 different color pebbles in a jar. 11 of them are blue and the rest are orange. Two pebbles are randomly selected from the jar, one at a time without replacement.
a) Find the probability of taking an orange pebble followed by a blue pebble.
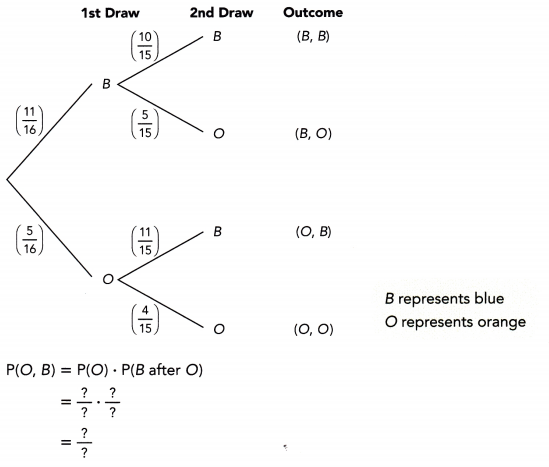
The probability of randomly taking an orange pebble followed by a blue pebble is ![]()
Answer:
P(B,O) = P(B) x P(O)
= 11/16 x 5/15
= 55/240
= 11/48
~0.23
Therefore, the probability of selecting a blue than a orange pebble is 11/48 or approx 0.23.
b) Find the probability of taking two orange pebbles.
P(O, O) = P(O) • P(O after O)
= \(\frac{?}{?} \cdot \frac{?}{?}\)
= \(\frac{?}{?}\)
The probability of randomly taking two orange pebbles is ![]() .
.
Answer:
P(O, O) = P(O) • P(O)
= 5/16 x 4/15
= 20/240
= 1/12
~0.08
Therefore, the probability of selecting two orange pebbles is 1/12 or approx 0.08.
c) Find the probability of taking two blue pebbles.
P(B, B) = P(B) • P(B after 8)
= \(\frac{?}{?} \cdot \frac{?}{?}\)
= \(\frac{?}{?}\)
The probability of randomly taking two blue pebbles is ![]() .
.
Answer:
P(B, B) = P(B) • P(B)
= 11/16 x 10/15
= 110/240
= 11/24
~0.46
The probability of randomly taking two blue pebbles is 11/24 or approx 0.46.
Question 3.
The tree diagram below shows how passing an examination depends on whether a student studies (S) or does not study (NS) for the exam. The probability that a student studies is denoted by p. Assume that S and NS are mutually exclusive events.
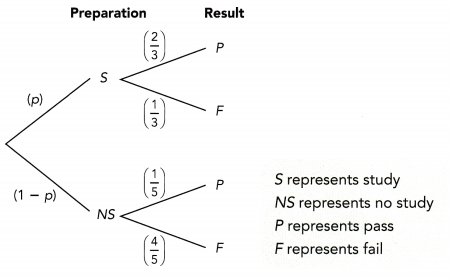
a) If p = 0.4, find the probability that a student passes the examination.
P(S) = \(\frac{?}{?}\) Write the fraction for 0.4.
P(NS) = 1 – P(S) Events S and NS are complementary.
= 1 – \(\frac{?}{?}\)
= \(\frac{?}{?}\)
P(P) = \(\frac{?}{?}\) • \(\frac{?}{?}\) + \(\frac{?}{?}\) • \(\frac{?}{?}\) Evaluate P(S, P) + P(NS, P).
= \(\frac{?}{?}\)
If the probability of studying is 0.4, then the probability of passing is ![]() .
.
Answer:
P(NS) + P(S) = 1
P(NS) = 1 – P(S)
P(NS) = 1 – 4/10
P(NS) = 6/10
Therefore, the probability of not studying is 6/10.
P(Pa) = P(S,P) + P(NS,P)
= P(S) x P(P) + P(NS) x P(P)
= 4/10 x 2/3 + 6/10 x 1/5
= 8/30 + 6/50
= 29/75
~0.39
Therefore, the probability of passing the exam is 29/75 or approx 0.39.
b) If p = 0.75, find the probability that a student fails the examination.
P(S) = \(\frac{?}{?}\) Write the fraction for 0.75.
P(NS) = 1 – P(S) Events S and NS are complementary.
= 1 – \(\frac{?}{?}\)
= \(\frac{?}{?}\)
P(F) = \(\frac{?}{?}\) • \(\frac{?}{?}\) + \(\frac{?}{?}\) • \(\frac{?}{?}\) Evaluate P(S, F) + P(NS, F).
= \(\frac{?}{?}\)
If the probability of studying is 0.75, then the probability of failing is ![]() .
.
Answer:
P(NS) + P(S) = 1
P(NS) = 1 – P(S)
P(NS) = 1 – 3/4
P(NS) = 1/4
Therefore, the probability of not studying is 1/4.
P(Fa) = P(S,F) + P(NS,F)
= P(S) x P(F) + P(NS) x P(F)
= 3/4 x 1/3 + 1/4 x 4/5
= 3/12 + 4/20
= 9/20
= 0.45
Therefore, the probability of failing the exam is 9/20 or approx is 0.45
Math in Focus Course 3B Practice 11.4 Answer Key
State whether each event is a dependent or independent event.
Question 1.
Drawing 2 red balls randomly, one at a time without replacement, from a bag of six balls.
Answer: Dependent event
Question 2.
Tossing a coin twice.
Answer: Independent event
Question 3.
Reaching school late or on time for two consecutive days.
Answer: Independent event
Question 4.
Flooding of roads during rainy or sunny days.
Answer: Dependent event
Draw the tree diagram for each compound event.
Question 5.
2 balls are drawn at random, one at a time without replacement, from a bag of 3 green balls and 18 red balls.
Answer:
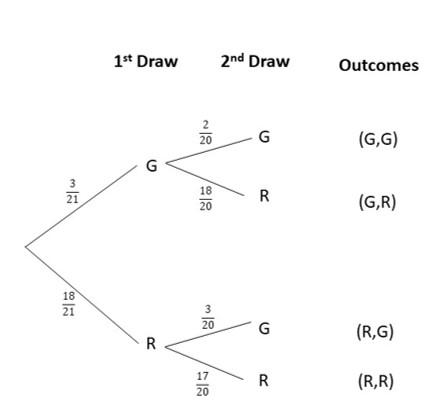
Question 6.
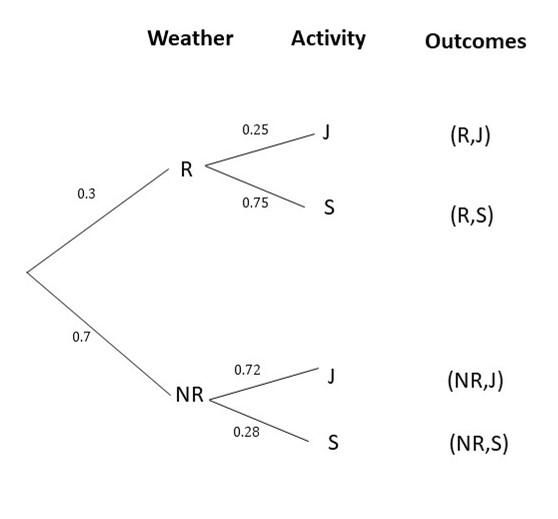
The probability of rain on a particular day is 0.3. If it rains, then the probability that Renee goes shopping is 0.75. If it does not rain, then the probability that she goes jogging is 0.72. Assume that shopping and jogging are mutually exclusive and that rain and no rain are complementary.
Answer:
The probability of raining is 0.3, and the probability of raining P(R) and the probability of not raining P(NR) is equal to 1, then
P(NR) + P(R) = 1
P(NR) = 1 – P(R)
P(NR) = 1 – 0.3
P(NR) = 0.7
Therefore, the probability of not raining is 0.7
The probability of shopping when rain comes is 0.75, and the probability of shopping P(S), when it rains and the probability of jogging P(J) during rainy day is equal to 1, then
P(S) + P(J) = 1
P(J) = 1 – P(S)
P(J) = 1 – 0.75
P(J) = 0.25
Therefore, the probability of jogging when rains is 0.25
The probability of jogging when the rain did not come is 0.72, and the probability of shopping P(S) when it did not rain and the probability of jogging P(J) during a non-rainy day is equal to 1, then
P(S) + P(J) = 1
P(S) = 1 – P(J)
P(S) = 1 – 0.72
P(S) = 0.28
Therefore, the probability of shopping when it did not rain is 0.28.
Solve. Show your work.
Question 7.
Geraldine has a box of 13 colored pens: 3 blue, 4 red, and the rest black. What is the probability of drawing two blue pens randomly, one at a time without replacement?

Answer:
P(B, B) = P(B) x P(B)
= 3/13 x 2/12
= 1/26.
Therefore, the probability of picking blue pens twice is 1/26.
Question 8.
A box contains 8 dimes, 15 quarters, and 27 nickels. A student is to randomly pick two items, one at a time without replacement, from the bag. Find the probability that 2 quarters are picked.
Answer:
P(Q,Q) = P(Q) x P(Q)
= 15/50 x 14/49
= 210/2450
= 3/35
Therefore, the probability of picking a quarter twice is 3/35.
Question 9.
There are 9 green, 2 yellow, and 5 blue cards in a deck. Players A and B each randomly pick a card from the deck. Player A picks a card first before player B picks. Find the probability that both players pick the same color cards.
Answer:
P(B,B) or P(Y,Y) or P(G,G) = P(B,B) + P(Y,Y) + P(G,G)
= P(B) x P(B) + P(Y) x P(Y) + P(G) x P(G)
= 5/16 x 4/15 + 2/16 x 1/15 + 9/16 x 8/15
= 20/240 + 2/240 + 72/240
= 94/240
= 47/120
Therefore, the probability of obtaining a matching color of cards is 47/120.
Question 10.
The probability diagram below shows the probability of Xavier going to library or park depending if the weather is sunny or rainy. The probability of rain on a particular day is denoted by a. Assume that going to the library and going to the park are mutually exclusive and complementary.
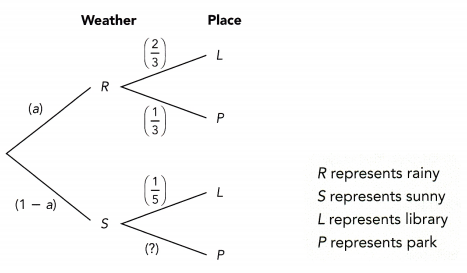
a) If a = 0.3, find the probability that Xavier goes to the park on any day.
Answer:
To convert decimals into fractions,
= 0.3/1
Multiplying both numerator and denominator to 100
= 0.3/1 x 100/100
= 30/100
= 3/10
Therefore, 0.3 is 3/10 in fractional form.
P(S) + P(R) = 1
P(S) = 1 – P(R)
P(S) = 1- 3/10
P(S) = 7/10
Therefore, the probability of having a sunny day is 7/10.
P(L) + P(P) = 1
P(P) = 1 – P(L)
P(P) = 1 – 1/5
P(P) = 4/5
Therefore, the probability of going to the park during the sunny day is 4/5.
P(S,P) or P(R,P) = P(S,P) + P(R,P)
= P(S) x P(P) + P(R) x P(P)
= 7/10 x 4/5 + 3/10 x 1/3
= 28/50 + 3/30
= 33/30
= 0.66
Therefore, the probability of going to park at any day is 0.66.
b) If a = 0.75, find the probability that he goes to the library on any day.
Answer:
Converting the decimals into fractions,
= 0.75/1
Multiply both the numerator and denominator to 100,
= 0.75/1 x 100/100
= 75/100
= 3/4
Therefore, 3/4 is the fractional form of 0.75
P(S) + P(R) = 1
P(S) = 1 – P(R)
P(S) = 1 – 3/4
P(S) = 1/4
Therefore, the probability of having a sunny day is 1/4.
P(S,L) or P(R,L) = P(S,L) + P(R,L)
= P(S) x P(L) + P(R) x P(L)
= 1/4 x 1/5 + 3/4 x 2/3
= 1/20 + 6/12
= 11/20
= 0.55
Therefore, the probability of going to library at any day is 0.55.
Question 11.
There are 15 apples in a fruit basket. 6 of them are red apples and the rest green apples. Two apples are picked randomly, one at a time without replacement.

a) Draw a tree diagram to represent the possible outcomes.
Answer:
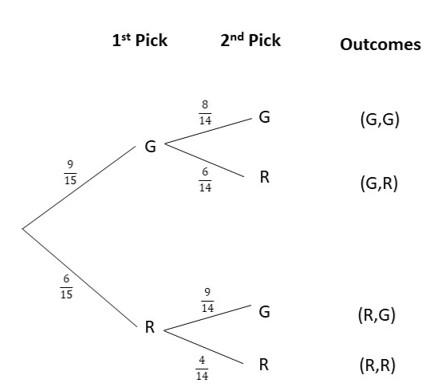
b) Find the probability of picking a green apple and then a red apple.
Answer:
P(G,R) = P(G) x P(R)
= 9/15 x 6/14
= 54/210
= 9/35
Therefore, the probability of picking a green apple then a red apple is 9/35.
c) Find the probability of picking two green apples.
Answer:
P(G,G) = P(G) x P(G)
= 9/15 x 8/14
= 72/210
= 12/35
Therefore, the probability of getting two green apples is 12/35.
d) Find the probability of picking two red apples.
Answer:
P(R,R) = P(R) x P(R)
= 6/15 x 5/14
= 30/210
= 1/70
Therefore, the probability of obtaining two red apples is 1/7.
Question 12.
There are 8 people in a room: 3 of them have red hair, 2 have blonde hair, and the rest have dark hair. Two people are randomly selected to leave the room, one after another, and they do not re-enter the room.
a) Draw a tree diagram to represent the possible outcomes.
Answer:
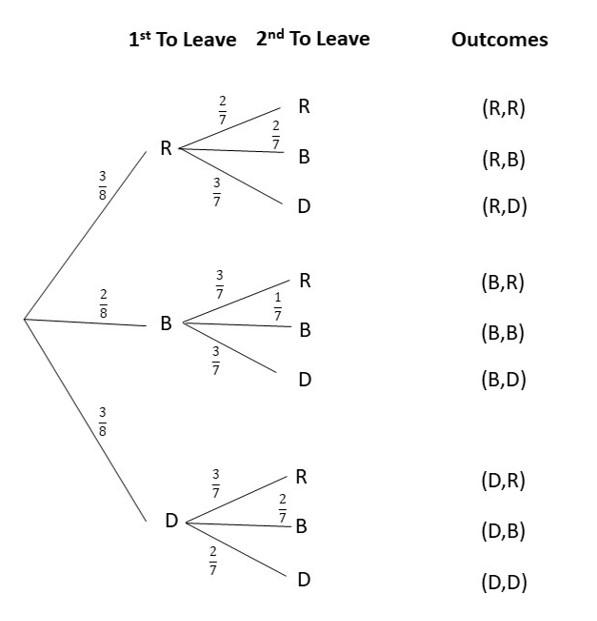
b) What is the probability of a person with dark hair leaving the room first?
Answer:
P(D,D) or P(D,R) or P(D,B) = P(D,D) + P(D,R) + P(D,B)
= P(D) x P(D) + P(D) x P(R) + P(D) x P(B)
= 3/8 x 2/7 + 3/8 x 3/7 + 3/8 x 2/7
= 6/56 + 9/56 + 6/56
= 21/56
= 3/8
Therefore, the probability that a dark haired person is the first one to leave is 3/8
c) What is the probability of a person with red hair leaving the room, followed by a person with blonde hair?
Answer:
P(R,B) = P(R) x P(B)
= 3/8 x 2/7
= 6/56
= 3/28
Therefore, the probability that a red haired person is the first one to leave then a blonde is 3/28.
d) What is the probability of two people with the same hair color leaving the room?
Answer:
P(D,D) or P(R,R) or P(B,B) = P(D,D) + P(R,R) + P(B,B)
= P(D) x P(D) + P(R) x P(R) + P(B) x P(B)
= 3/8 x 2/7 + 3/8 x 2/7 + 2/8 x 1/7
= 6/56 + 9/56 + 2/56
= 17/56
Therefore, the probability that a dark haired person is the first to leave is 17/56.
Question 13.
Along a stretch of road there are 2 traffic light intersections. Having red or green light for the first intersection is equally likely. Having a red light at the second intersection is twice as likely as a green light, if the first intersection traffic light was red. What is the probability of having a red light on the first intersection and a green light on the second intersection? Draw a tree diagram to show the possible outcomes.
Answer:
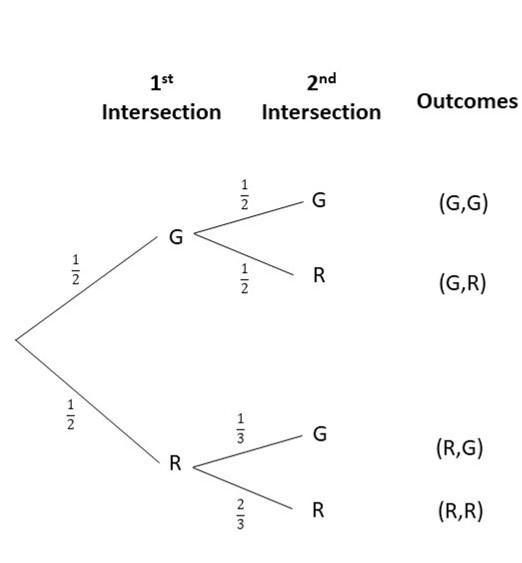
P(R,G) = P(R) x P(G)
= 1/2 x 1/3
= 1/6
Therefore, the probability of encountering a red then a green light is 1/6.
Question 14.
To get to work, Mr. Killiney needs to take a train and then a bus. The probability that the train breaks down is 0.1. When the train breaks down, there is a 0.7 probability that the bus will be overcrowded. When the train is operating normally, there is a 0.2 probability that the bus will be overcrowded. What is the probability of getting a seat in the bus? Draw a tree diagram to show the possible outcomes.
Answer:
P(SW) + P(W) = 1
P(W) = 1 – P(SW)
P(W) = 1 – 0.1
P(W) = 0.9
Therefore, the probability of the train working normally is 0.9.
P(NF) + P(F) = 1
P(NF) = 1 – P(F)
P(NF) = 1 – 0.7
P(NF) = 0.3
Therefore, the probability that the bus is not full is 0.3 when the train is not working properly.
P(NF) + P(F) = 1
P(NF) = 1- P(F)
P(NF) = 1 – 0.2
P(NF) = 0.8
Therefore, the probability that the bus is not full is 0.8 when the train is not working properly.
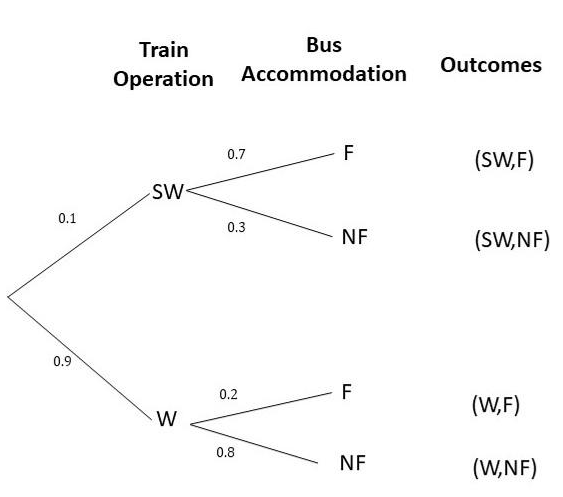
P(SW,NF) or P(W,NF) = P(SW) x P(NF) + P(W) x P(NF)
= 0.1 x 0.3 + 0.9 x 0.8
= 0.03 + 0.72
= 0.75
Therefore, the probability that the bus is not full is 0.75.
Brain @ Work
Question 1.
If there are 12 green and 6 red apples, find the probability of randomly choosing three apples of the same color in a row, without replacement. Show your work.
Answer:
P(G,G,G) = P(G) x P(G) x P(G)
= 12/18 x 11/17 x 10/16
= 55/204
Therefore, the probability of obtaining green apples is 55/204.
P(R,R,R) = P(R) x P(R) x P(R)
= 6/18 x 5/17 x 4/16
= 5/204
Therefore, the probability of obtaining red apples is 5/204.
P(R,R,R) or P(G,G,G) = P(R) x P(R) x P(R) + P(G) x P(G) x P(G)
= 5/204 + 55/204
= 60/204
= 5/17
Therefore, the probability of obtaining of picking 3 apples of a matching color is 5/17.
Question 2.
William has five $1 bills, ten $10 bills, and three $20 bills in his wallet. He picks three bills randomly in a row, without replacement. What is the probability of him picking three of the same type of bills? $how your work.
Answer:
P($20,$20,$20) = P($20) x P($20) x P($20)
= 3/18 x 2/17 x 1/16
= 6/4896
= 1/816
Therefore, the probability of obtaining three $20 bills is $1/816.
P($10,$10,$10) = P($10) x P($10) x P($10)
= 10/18 x 9/17 x 8/16
= 720/4896
= 5/34
Therefore, the probability of obtaining three $10 bills is $5/34.
P($1,$1,$1) = P($1) x P($1) x P($1)
= 5/18 x 4/17 x 3/16
= 60/4896
= 5/408
Therefore, the probability of obtaining three $1 bills is 5/408.
P($20,$20,$20) or P($10,$10,$10) or P($1,$1,$1) = P($20,$20,$20) + P($10,$10,$10) + P($1,$1,$1)
= 1/816 + 5/34 + 5/408
= 131/816
Therefore, the probability of having three bills of a matching type is 131/816.
Question 3.
Daniel plans to visit Australia. Whether he goes alone or with a companion is equally likely. If he travels with a companion there is a 40% chance of joining a guided tour. If he travels alone, there is an 80% chance of joining a guided tour.

a) What is the probability of traveling with a companion and not joining a guided tour?
Answer:
P(NT) + P(T) = 1
P(NT) = 1 – P(T)
P(NT) = 1 – 0.4
P(NT) = 0.6
Therefore, the probability of not going to tour is 0.6 if he travels with others.
P(NT) + P(T) = 1
P(NT) = 1 – P(T)
P(NT) = 1 – 0.8
P(NT) = 0.2
Therefore, the probability of not going to tour is 0.2 if he travels without the other.
P(C,NT) = P(C) x P(NT)
= 0.5 x 0.6
= 0.3
Therefore, the probability of travelling with others and not going with a tour is 0.3.
b) What is the chance of joining a guided tour?
Answer:
P(C,T) or P(WC,T) = P(C) x P(T) + P(WC) x P(T)
= 0.5 x 0.4 + 0.5 x 0.8
= 0.2 + 0.4
= 0.6
Therefore, the probability of being in a tour is 0.6