Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 10 Practice 2 Expressing Fractions as Percents to score better marks in the exam.
Math in Focus Grade 5 Chapter 10 Practice 2 Answer Key Expressing Fractions as Percents
Express each fraction as a percent.
Example
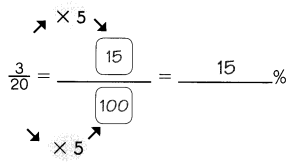
Question 1.
\(\frac{26}{50}\) = ______%
Answer: 15%
Explanation:
To convert a fraction to a percent, first multiply the numerator and the denominator with 5.
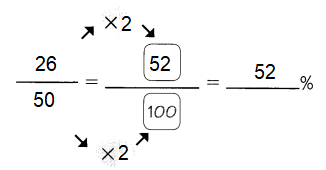
Question 2.
\(\frac{4}{5}\) = ______%
Answer: 25%
Explanation:
To convert a fraction to a percent, first multiply the numerator and the denominator with 25.
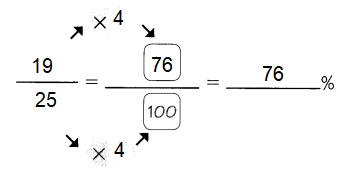
Question 3.
\(\frac{19}{25}\) = ______%
Answer: 76%
Explanation:
To convert a fraction to a percent, first multiply the numerator and the denominator with 4.
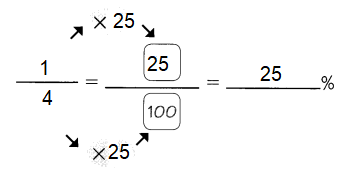
Question 4.
\(\frac{1}{4}\) = ______%
Answer: 25%
Explanation:
To convert a fraction to a percent, first multiply the numerator and the denominator with 25.

Express each fraction as a percent.
Example
\(\frac{1}{5}\) = \(\frac{1}{5}\) × 100% = 20
Question 5.
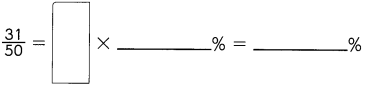
Answer:
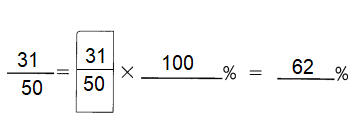
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the decimal by 100 to express fraction as percentage.
Question 6.
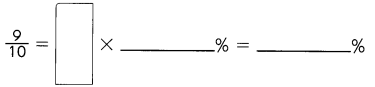
Answer:
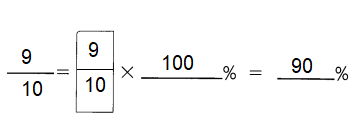
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the decimal by 100 to express fraction as percentage.
Question 7.
Answer:
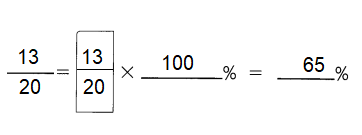
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the decimal by 100 to express fraction as percentage.
Express each percent as a fraction in simplest form.
Example
Question 8.
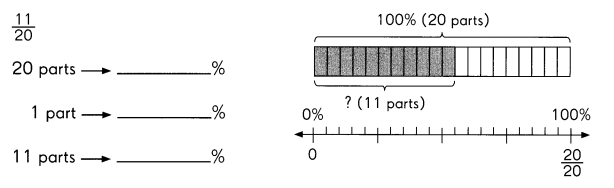
Answer:
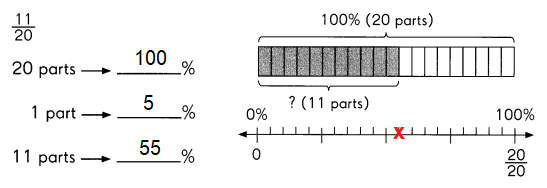
Explanation:
To convert a percent to a fraction, we have to remove the percent sign and divide the given number by 100.
And, then we express the fractional form of the percentage in the simplest form.
Divide 100% into 20 parts as each part has 5%.
So, 11 parts is equal to 55%.
Question 9.
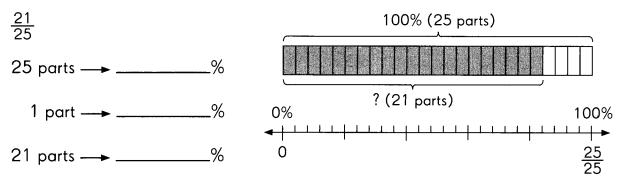
Answer:
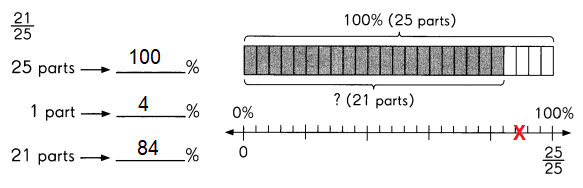
Explanation:
To convert a percent to a fraction, we have to remove the percent sign and divide the given number by 100.
And, then we express the fractional form of the percentage in the simplest form.
Divide 100% into 25 parts as each part has 4%.
So, 21 parts is equal to 84%.
Express each fraction as a percent.
Question 10.
\(\frac{64}{200}\) = \(\frac{32}{100}\) = ___ %
Answer: 32 %
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .
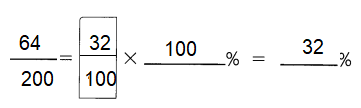
Question 11.
\(\frac{1300}{400}\) = ___ %
Answer: 325%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .
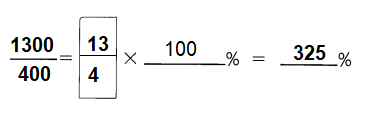
Question 12.
\(\frac{480}{600}\) = ___ %
Answer: 80%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .
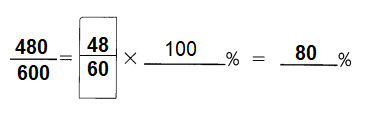
Question 13.
\(\frac{518}{700}\) = ___ %
Answer: 74%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .
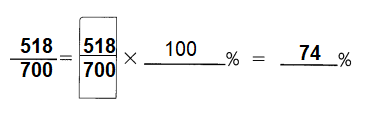
Solve. Show your work.
Question 14.
Jeremy finished \(\frac{3}{5}\) of his homework. What percent of his homework did he finish?

Answer: 60%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .
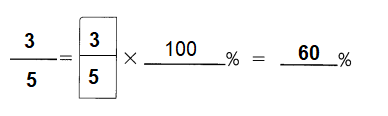
Question 15.
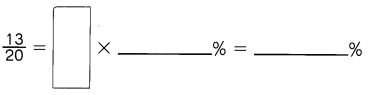
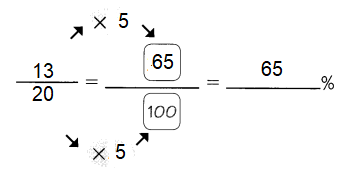
Tracy ran in a marathon, but managed to complete only \(\frac{13}{20}\) of the race.
a. What percent of the marathon did she complete?
Answer: 65%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .
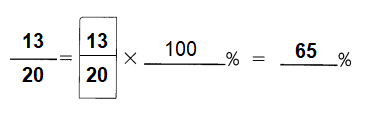
b. Write each ratio as a fraction and then as a percent.
Answer:
\(\frac{65}{100}\) = 65 %
Explanation:
To convert a fraction to a percent, first multiply the numerator and the denominator with 5.
Solve. Show your work.
Question 16.
Katie bought some flour. She used \(\frac{3}{8}\) of it to bake bread. What percent of the flour is left?
Answer: 62.5%
Explanation:
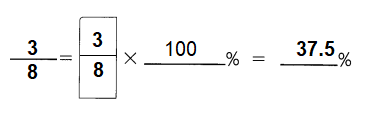
She used \(\frac{3}{8}\) of it to bake bread, it means 37.5% used
100% – 37.5% = 62.5% of the flour is left.
Question 17.
There are 800 members in on astronomy club, and 320 of them are females. What percent of the members are males?
Answer: 60%
Explanation:
800 members in on astronomy club, and 320 of them are females.
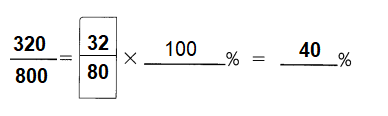
it means 40% are females.
100 % – 40% = 60% of the members are males.