Math in Focus Grade 7 Cumulative Review Chapters 1-2 Answer Key

Go through the Math in Focus Grade 7 Workbook Answer Key Cumulative Review Chapters 1-2 to finish your assignments.

Math in Focus Grade 7 Course 2 A Cumulative Review Chapters 1-2 Answer Key

Concepts and Skills

Write each number as \(\frac{m}{n}\) in simplest form, where m and n are integers with n ≠ 0. (Lesson 1.1)

Question 1.
-0.87
Answer:
0.87 can be written in the \(\frac{m}{n}\) form as –\(\frac{87}{100}\)

Question 2.
12.8
Answer:
12.8 can be written in the \(\frac{m}{n}\) form as \(\frac{128}{10}\) or \(\frac{64}{5}\)

Question 3.
-1.9
Answer:
-1.9 can be written in the \(\frac{m}{n}\) form as \(\frac{-19}{10}\)

Using long division, write each rational number as a terminating or a repeating decimal. Identify a pattern of repeating digits using bar notation. (Lesson 1.2)

Question 4.
\(\frac{9}{5}\)
Answer: \(1 . \overline{8}\)

Question 5.
\(\frac{23}{16}\)
Answer: 1.4375 it is a terminating decimal

Question 6.
–\(\frac{51}{110}\)
Answer: \(0 . 46\overline{36}\)

Use a calculator. Locate each irrational number to 2 decimal places on the number line using rational approximations. (Lesson 1.3)

Question 7.
\(\sqrt{44}\)
Answer: 6.63

Question 8.
\(\sqrt{132}\)
Answer: 11.48

Question 9.
–\(\sqrt{162}\)
Answer: 12.72

Question 10.

Answer: 4.64

Question 11.
\(\frac{\pi}{7}\)
Answer: 0.44

Question 12.
π³
Answer: 30.95

Order the real numbers below from greatest to least using the symbol >. (Lesson 1.4)

Question 13.
\(\sqrt{345}\), \(\frac{244}{7}\), , –\(\frac{86}{3}\), 33.9
Answer:\(\frac{244}{7}\) > 33.9> \(\sqrt{345}\)>>-\(\frac{86}{3}\)

Round each number to the given number of significant digits. (Lesson 1.5)

Question 14.
349,950 (to 4 significant digits)
Answer: 350000

Question 15.
0.09608 (to 3 significant digits)
Answer: 0.0961

Evaluate each expression. (Lessons 2.1, 2.2)

Question 16.
7 + (-12)
Answer:
7 – 12 = -5

Question 17.
-15 + (-20)
Answer:
-15 – 20 = -35

Question 18.
-8 + 6 – 4
Answer:
– 8 – 4 + 6
-12 + 6 = -6

Question 19.
11 – (-14)
Answer:
11 – (-14)
– × – = +
11 + 14 = 25

Question 20.
32 – (-17)
Answer:
32 – (-17)
– × – = +
32 + 17 = 39

Question 21.
-7 – 5 – (-6)
Answer:
-7 – 5 – (-6)
-7 – 5 + 6
-12 + 6 = -6

Question 22.
-250 + 480
Answer:
-250 + 480
480 – 250 = 230
The greatest value has a positive sign so put a positive sign to the obtained answer.
-250 + 480 = 230

Question 23.
-109 – (-121)
Answer:
-109 – (-121)
-109 + 121
The greatest value has a positive sign so put a positive sign to the obtained answer.
121 – 109 = 12

Question 24.
43 + (-95) – (-16)
Answer:
43 + (-95) – (-16)
43 – 95 + 16
43 + 16 – 95 = -36

Evaluate each product or quotient. As needed, give your answer in simplest form. (Lessons 2.3, 2.5)

Question 25.
-12.8
Answer:
– × + = –
12 × 8 = 96
Put negative sign to the obtained answer.
We get -96

Question 26.
\(\frac{2}{15} \cdot\left(-\frac{5}{8}\right)\)
Answer:
– × + = –
\(\frac{2}{15}\) × –\(\frac{5}{8}\) = –\(\frac{10}{120}\) = \(\frac{1}{12}\)

Question 27.
\(2 \frac{2}{5} \cdot\left(-1 \frac{1}{4}\right)\)
Answer:
– × + = –
2\(\frac{2}{5}\) × -1\(\frac{1}{4}\)
\(\frac{12}{5}\) × –\(\frac{5}{4}\)
= –\(\frac{60}{20}\)
= -3

Question 28.
-9 ÷ (-7)
Answer:
Cancel – by –
9 ÷ 7 = 1.28

Question 29.
\(-\frac{7}{16} \div\left(-\frac{21}{6}\right)\)
Answer:
Given,
\(\frac{7}{16}\) × –\(\frac{21}{6}\)
= \(\frac{7}{16}\) × –\(\frac{7}{2}\)
= –\(\frac{49}{32}\)

Question 30.

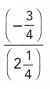
Answer:
–\(\frac{3}{4}\) × 2\(\frac{1}{4}\)
= –\(\frac{3}{4}\) × \(\frac{9}{4}\)
= – \(\frac{27}{16}\)

Evaluate each expression. (Lessons 2.3, 2.4, 2.5, 2.6)

Question 31.
-3 • 12 – (-6) + 2(-7) ÷ 7
Answer:
-3 • 12 – (-6) + 2(-7) ÷ 7
((-3) 12) – (-6) + ((2 * (-7)/7))
= -32

Question 32.
\(\frac{2}{3}\) • \(\frac{1}{6}\) + 1\(\frac{5}{9}\) + 2\(\left(-\frac{7}{18}\right)\)
Answer:
Given,
\(\frac{2}{3}\) • \(\frac{1}{6}\) + 1\(\frac{5}{9}\) + 2\(\left(-\frac{7}{18}\right)\)
\(\frac{2}{18}\) + \(\frac{14}{9}\) – \(\frac{43}{18}\)
– \(\frac{41}{18}\) + \(\frac{14}{9}\)
= – \(\frac{41}{18}\) + \(\frac{28}{18}\)
= –\(\frac{13}{18}\)

Question 33.
-4 • 5.2 – 0.5• (-7.8) + 2 • 1.3
Answer: -14.3

Question 34.
–\(\frac{1}{5}\) [-20 + 1.2(-3)] + 1\(\frac{2}{5}\)
Answer:
Given,
–\(\frac{1}{5}\) [-20 + 1.2(-3)] + 1\(\frac{2}{5}\)
–\(\frac{1}{5}\) [-20 – 3.6] + 1\(\frac{2}{5}\)
–\(\frac{1}{5}\) [-23.6] + 1\(\frac{2}{5}\)
4.72 + \(\frac{7}{5}\)
4.72 + 1.4
= 6.12

Problem Solving

Solve. Show your work.

Question 35.
An athlete completes a 400-meter dash in 46.3 seconds. What is his speed in meters per second correct to 3 significant digits? (Chapter 1)
Answer:
An athlete completes a 400-meter dash in 46.3 seconds.
400/46.3
8.639
8.64 m/s

Question 36.
The greatest and least temperatures ever recorded in Tim’s hometown are 101°F and -36°F. Find the difference between these two temperatures. (Chapter 2)
Answer:
Given,
The greatest and least temperatures ever recorded in Tim’s hometown are 101°F and -36°F.
101°F – (-36°F)
= 101°F + 36°F
= 137°F

Question 37.
On a math quiz consisting of 100 questions, the teacher gives 2 points for a correct answer, -1 point for an incorrect answer, and -2 points for not answering a question at all. (Chapter 2)
a) Emily answered 75 questions correctly, 18 incorrectly, and did not answer 7 questions. What is her score?
Answer:
75 × 2 = 150
18 × -1 = -18
7 × -2 = -14
150 -18 – 14
150 – 32 = 118
Thus the score of Emily is 118

b) Amy answered 30 questions correctly and 62 incorrectly. What is her score?
Answer:
30 × 2 = 60
62 × – 1 = -62
60 – 62 = -2
Amy score is -2

Question 38.
Justin dug a hole that was 9\(\frac{1}{2}\) inches deep. His sister Jean built a sand castle next to the hole that was 12\(\frac{3}{4}\) inches high. Show how you could use subtraction to find the vertical distance from the top of the castle to the bottom of the hole. (Chapter 2)
Answer:
Justin dug a hole that was 9\(\frac{1}{2}\) inches deep.
His sister Jean built a sand castle next to the hole that was 12\(\frac{3}{4}\) inches high.
12\(\frac{3}{4}\) – 9\(\frac{1}{2}\)
12 – 9 = 3
\(\frac{3}{4}\) – \(\frac{1}{2}\)  = \(\frac{1}{4}\)
= 3\(\frac{1}{4}\) inches

Question 39.
Rick started his hike at an elevation of 8,975 feet. He descended at a constant rate of 8.5 feet per minute for 45 minutes. Find Rick’s elevation after 45 minutes. Give your answer to 4 significant digits. (Chapters 1, 2)
Answer:
Given,
Rick started his hike at an elevation of 8,975 feet.
He descended at a constant rate of 8.5 feet per minute for 45 minutes.
8.5 × 45 = 382.5 feet
8975 feet – 382.5 feet = 8592.5 feet
8593 feet

Question 40.
A car travels’at 68\(\frac{2}{3}\) miles per hour for 2\(\frac{1}{12}\) hours. Find the distance that the car has traveled correct to 3 significant digits. (Chapters 1, 2)
Answer: 68\(\frac{2}{3}\) × 2\(\frac{1}{12}\)
= 143 \(\frac{1}{18}\)
= 143.055

Question 41.
In a particular town, the temperature at midnight is -2°C. It rises at a steady rate for 12 hours to reach a temperature of 22°C at noon. (Chapter 2)
a) Find the difference between the temperature at noon and at midnight.
Answer: 24°C

b) Find the temperature at 7 A.M.
Answer: 12°C

c) Find the time when the temperature is 4°C.
Answer: 3 A.M.