Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Lesson 3.1 Adding Algebraic Terms to finish your assignments.
Math in Focus Grade 7 Course 2 A Chapter 3 Lesson 3.1 Answer Key Adding Algebraic Terms
Math in Focus Grade 7 Chapter 3 Lesson 3.1 Guided Practice Answer Key
Copy and complete to simplify each expression.
Question 1.
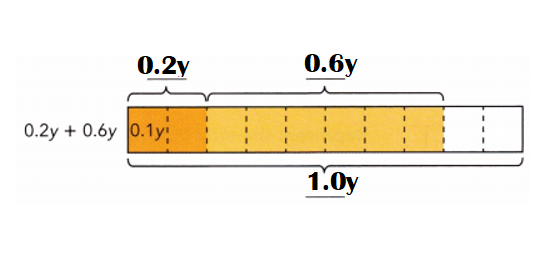
0.2y + 0.6y
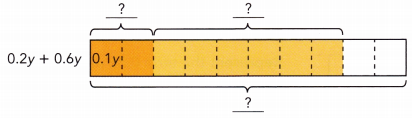
0.2y + 0.6y = ![]()
Answer:
0.2y + 0.6y = 0.8y.
Explanation:
Question 2.
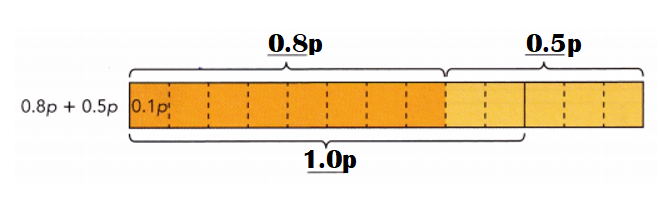
0.8p + 0.5p
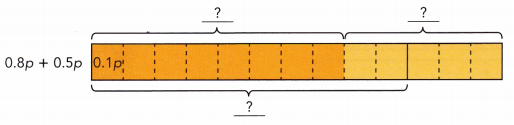
0.8 p + 0.5p = ![]()
Answer:
0.8 p + 0.5p = 1.3p.
Explanation:
Question 3.
1.3g + 0.9g
1.3g + 0.9g = ![]()
Answer:
1.3g + 0.9g = 2.2g.
Explanation:
1.3g + 0.9g = 2.2g.
Copy and complete to simplify each expression.
Question 4.
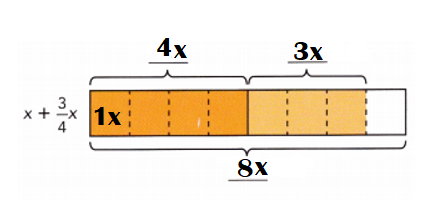
x + \(\frac{3}{4}\)x
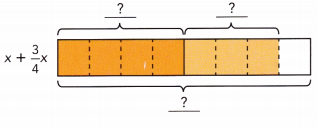
x + \(\frac{3}{4}\)x = ![]()
Answer:
Explanation:
x + \(\frac{3}{4}\)x = (4x + 3x) ÷ 4
= 7x ÷ 4 or \(\frac{7}{4}\)x
Question 5.
\(\frac{1}{2}\)p + \(\frac{2}{5}\)p
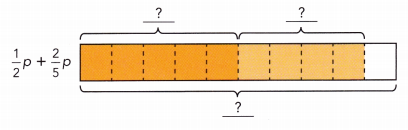
The LCD of \(\frac{1}{2}\) and \(\frac{2}{5}\) is ![]() .
.
So, p is divided into ![]() p sections.
p sections.
\(\frac{1}{2}\)p + \(\frac{2}{5}\)p = ![]()
Answer:
\(\frac{1}{2}\)p + \(\frac{2}{5}\)p = \(\frac{15}{10}\)p
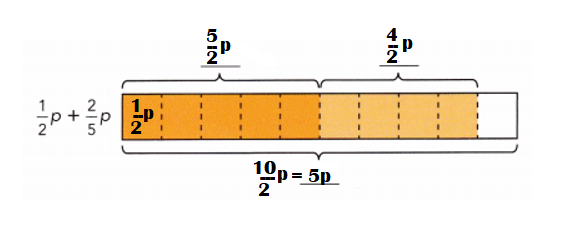
Explanation:
The LCD of \(\frac{1}{2}\) and \(\frac{2}{5}\) is 10.
So, p is divided into 10 p sections.
\(\frac{1}{2}\)p + \(\frac{2}{5}\)p
= [(1 ×5)p + (2 × 5)p] ÷ 10
= (5p + 10p) ÷ 10
= 15p ÷ 10 or \(\frac{15}{10}\)p
Simplify each expression.
Question 6.
m + \(\frac{5}{6}\)m
Answer:
m + \(\frac{5}{6}\)m = \(\frac{11}{6}\)m
Explanation:
m + \(\frac{5}{6}\)m
= (6m + 5m) ÷ 6
= 11m ÷ 6 or \(\frac{11}{6}\)m.
Question 7.
\(\frac{1}{4}\)x + \(\frac{2}{3}\)x
Answer:
\(\frac{1}{4}\)x + \(\frac{2}{3}\)x = \(\frac{7}{12}\)x
Explanation:
\(\frac{1}{4}\)x + \(\frac{2}{3}\)x
= LCM of 4 n 3 = 12.
\(\frac{1}{4}\)x + \(\frac{2}{3}\)x
= [(1 × 3) + (2 × 4)]x ÷ 12
= (3 + 4)x ÷ 12
= 7x ÷ 12 or \(\frac{7}{12}\)x
Question 8.
Math Journal In questions 5 and 7 you can multiply the two denominators to get the LCD. Does this always work? Explain.
Answer:
You can multiply the two denominators to get the LCD because there is no common factors between the denominators, so you can multiply the numbers to simplify the problem.
Explanation:
Question5:
\(\frac{1}{2}\)p + \(\frac{2}{5}\)p
LCD of 2 n 5 = 2 × 5 = 10.
Question7:
\(\frac{1}{4}\)x + \(\frac{2}{3}\)x
LCD of 4 n 3 = 4 × 3 = 12.
Math in Focus Course 2A Practice 3.1 Answer Key
Simplify each expression with decimal coefficients.
Question 1.
0.5y + 0.2y
Answer:
0.5y + 0.2y = 0.7y.
Explanation:
0.5y + 0.2y = 0.7y.
Question 2.
0.2x + 0.8x
Answer:
0.2x + 0.8x = 1.0x.
Explanation:
0.2x + 0.8x = 1.0x.
Question 3.
x + 0.6x
Answer:
x + 0.6x = 1.6x.
Explanation:
x + 0.6x
= 1x + 0.6x
= 1.6x.
Question 4.
0.4a + 1.2a
Answer:
0.4a + 1.2a = 1.6a.
Explanation:
0.4a + 1.2a = 1.6a.
Question 5.
0.7b + 0.9b
Answer:
0.7b + 0.9b = 1.6b.
Explanation:
0.7b + 0.9b = 1.6b
Question 6.
0.6m + 0.8m
Answer:
0.6m + 0.8m = 1.4m.
Explanation:
0.6m + 0.8m = 1.4m.
Question 7.
0.5k + 1.6k
Answer:
0.5k + 1.6k = 2.1k.
Explanation:
0.5k + 1.6k = 2.1k.
Question 8.
0.8a + 1.8a
Answer:
0.8a + 1.8a = 2.6a.
Explanation:
0.8a + 1.8a = 2.6a.
Simplify each expression with fractional coefficients.
Question 9.
\(\frac{1}{5}\)x + \(\frac{2}{5}\)x
Answer:
\(\frac{1}{5}\)x + \(\frac{2}{5}\)x = \(\frac{3}{5}\)x
Explanation:
\(\frac{1}{5}\)x + \(\frac{2}{5}\)x
= [(1 + 2)x] ÷ 5
= 3x ÷ 5
= \(\frac{3}{5}\)x
Question 10.
\(\frac{3}{7}\)p + \(\frac{2}{7}\)p
Answer:
\(\frac{3}{7}\)p + \(\frac{2}{7}\)p = \(\frac{5}{7}\)p
Explanation:
\(\frac{3}{7}\)p + \(\frac{2}{7}\)p
= [(3 + 2)p] ÷ 7
= 5p ÷ 7
= \(\frac{5}{7}\)p
Question 11.
\(\frac{5}{8}\)m + \(\frac{7}{8}\)m
Answer:
\(\frac{5}{8}\)m + \(\frac{7}{8}\)m = \(\frac{3}{2}\)m
Explanation:
\(\frac{5}{8}\)m + \(\frac{7}{8}\)m
= (5 + 7)m ÷ 8
= 12m ÷ 8
= 6m ÷ 4
= 3m ÷ 2
= \(\frac{3}{2}\)m
Question 12.
\(\frac{4}{9}\)n + \(\frac{7}{9}\)n
Answer:
\(\frac{4}{9}\)n + \(\frac{7}{9}\)n = \(\frac{13}{9}\)n.
Explanation:
\(\frac{4}{9}\)n + \(\frac{7}{9}\)n
= (4 + 9)n ÷ 9
= 13n ÷ 9
= \(\frac{13}{9}\)n
Simplify each expression with fractional coefficients by rewriting the fractions.
Question 13.
\(\frac{1}{6}\)a + \(\frac{1}{3}\)a
Answer:
\(\frac{1}{6}\)a + \(\frac{1}{3}\)a = \(\frac{1}{2}\)a
Explanation:
\(\frac{1}{6}\)a + \(\frac{1}{3}\)a
= LCD of 6 n 3 = 3.
= (1 + 2)a ÷ 6
= 3a ÷ 6
= a ÷ 2 or \(\frac{1}{2}\)a
Question 14.
\(\frac{1}{2}\)k + \(\frac{3}{8}\)k
Answer:
\(\frac{1}{2}\)k + \(\frac{3}{8}\)k =
Explanation:
\(\frac{1}{2}\)k + \(\frac{3}{8}\)k
= LCD of 2 n 8 = 8.
= (4 + 3)k ÷ 8
= 7k ÷ 8 or \(\frac{7}{8}\)k
Question 15.
\(\frac{2}{5}\)p + \(\frac{7}{10}\)p
Answer:
\(\frac{2}{5}\)p + \(\frac{7}{10}\)p = \(\frac{11}{10}\)p
Explanation:
\(\frac{2}{5}\)p + \(\frac{7}{10}\)p
= LCD of 5 n 10 = 10.
= [(2 ×2) + 7]p ÷ 10
= (4 + 7)p ÷ 10
= 11p ÷ 10 or \(\frac{11}{10}\)p
Question 16.
\(\frac{7}{9}\)r + \(\frac{2}{3}\)r
Answer:
\(\frac{7}{9}\)r + \(\frac{2}{3}\)r = \(\frac{13}{9}\)r
Explanation:
\(\frac{7}{9}\)r + \(\frac{2}{3}\)r
= LCD of 9 n 3 = 9.
= [7 + (2 × 3)]r ÷ 9
= (7 + 6)r ÷ 9
= 13r ÷ 9 or \(\frac{13}{9}\)r
Question 17.
\(\frac{1}{4}\)a + \(\frac{1}{3}\)a
Answer:
\(\frac{1}{4}\)a + \(\frac{1}{3}\)a = \(\frac{7}{12}\)a
Explanation:
\(\frac{1}{4}\)a + \(\frac{1}{3}\)a
= LCD of 4 n 3 = 12.
= [(1 × 3) + (1 × 4)]a ÷12
= (3 + 4)a ÷ 12
= 7a ÷ 12 or \(\frac{7}{12}\)a
Question 18.
\(\frac{1}{2}\)x + \(\frac{2}{5}\)x
Answer:
\(\frac{1}{2}\)x + \(\frac{2}{5}\)x = \(\frac{9}{10}\)x
Explanation:
\(\frac{1}{2}\)x + \(\frac{2}{5}\)x
= LCD of 2 n 5 = 10.
= [(1 × 5) + (2 × 2)]x ÷ 10
= (5 + 4)x ÷ 10
= 9x ÷ 10 or \(\frac{9}{10}\)x
Question 19.
\(\frac{3}{5}\)p + \(\frac{3}{4}\)p
Answer:
\(\frac{3}{5}\)p + \(\frac{3}{4}\)p = \(\frac{27}{20}\)p
Explanation:
\(\frac{3}{5}\)p + \(\frac{3}{4}\)p
= LCD of 5 n 4 = 20.
= [(3 × 4) + (3 × 5)]p ÷ 20
= (12 + 15)p ÷ 20
= 27p ÷ 20 or \(\frac{27}{20}\)p
Question 20.
\(\frac{4}{5}\)y + \(\frac{1}{3}\)y
Answer:
\(\frac{4}{5}\)y + \(\frac{1}{3}\)y = \(\frac{17}{15}\)y
Explanation:
\(\frac{4}{5}\)y + \(\frac{1}{3}\)y
= LCD of 5 n 3 = 15.
= [(4 × 3) + (1 × 5)]y ÷ 15
= (12 + 5)y ÷ 15
= 17y ÷ 15 or \(\frac{17}{15}\)y
Solve. Show your work.
Question 21.
The figures show rectangle A and rectangle B. Write and simplify an algebraic expression for each of the following.
a) The perimeter of rectangle A.
Answer:
Perimeter of rectangle A = \(\frac{28}{3}\)m
Explanation:
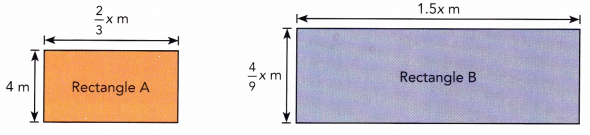
Perimeter of rectangle A = 2(Length + Width)
= 2(\(\frac{2}{3}\)m + 4m)
= 2[(2 + 12)m ÷ 3]
= 2(14m ÷ 3)
= 28m ÷ 3 or \(\frac{28}{3}\)m
b) The perimeter of rectangle B.
Answer:
Perimeter of rectangle B = \(\frac{35}{9}\)m
Explanation:

Perimeter of rectangle B = 2(Length + Width)
= 2(1.5m + \(\frac{4}{9}\)m)
= 2[(1.5 × 9) + 4)m ÷ 9]
= 2[(13.5 + 4) ÷ 9]m
= 2(17.5m ÷ 9)
= 35m ÷ 9 or \(\frac{35}{9}\)m
c) The sum of the perimeters of the two rectangles.

Answer:
Sum of the perimeters of the two rectangles = \(\frac{119}{9}\)m.
Explanation:
Perimeter of rectangle A = \(\frac{28}{3}\)m
Perimeter of rectangle B = \(\frac{35}{9}\)m
Sum of Perimeter of rectangle A n Perimeter of rectangle B
= \(\frac{28}{3}\)m + \(\frac{35}{9}\)m
LCD of 3 n 9 = 9.
= [(28 × 3) + (35 × 1)]m ÷ 9
= (84 + 35)m ÷ 9
= 119m ÷ 9 or \(\frac{119}{9}\)m
Question 22.
The length and width of two rectangular gardens are shown. Find the sum of the areas of the two gardens in simplest form.
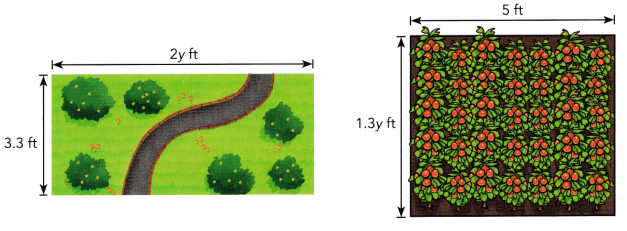
Answer:
Sum of the areas of the two gardens = 13.1y ft.
Explanation:
Area of rectangular garden 1 = Length × Width
= 2y ft × 3.3 ft
= 6.6y square ft.
Area of rectangular garden 2 = Length × Width
= 5y ft × 1.3y ft
= 6.5y square ft.
Sum of Area of rectangular garden 1 and Area of rectangular garden 2
= 6.6y square ft + 6.5y square ft
= 13.1y square ft.
Question 23.
Math Journal James and Evan simplified the same algebraic expression. Their work is shown.
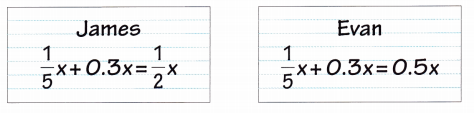
Describe a method each person might have used to get his answer. Which method do you prefer? Why?
Answer:
Both the method are easy to solve. I would like to prefer to simplified method.
Explanation:
James algebraic expression: Simplified method
\(\frac{1}{5}\)x + 0.3x = \(\frac{1}{2}\)x.
Evan algebraic expression: Fractional method
\(\frac{1}{5}\)x + 0.3x = 0.5x.
Question 24.
Which of the following expressions has a greater value if y is a positive number? Explain your reasoning.
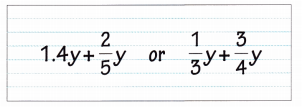
Answer:
1.4y + \(\frac{2}{5}\)y has a greater value if y is a positive number.
Explanation:
Expression 1:
1.4y + \(\frac{2}{5}\)y
If y = 1.
= (1.4 × 1) + \(\frac{2}{5}\) × 1
= 1.4 + \(\frac{2}{5}\)
= [(1.4 × 5) + 2] ÷ 5
= (7 + 2) ÷ 5
= 9 ÷ 5 or \(\frac{9}{5}\)
= 1.8.
Expression 2:
\(\frac{1}{3}\)y + \(\frac{3}{4}\)y
If y = 1.
= [\(\frac{1}{3}\) × 1] + \(\frac{3}{4}\) × 1
= \(\frac{1}{3}\) + \(\frac{3}{4}\)
LCD of 3 n 4 = 12.
= [(1 × 4) + (3 × 3)] ÷ 12
= (4 + 9) ÷ 12
= 13 ÷ 12 or \(\frac{13}{12}\)
= 1.08.
Question 25.
A restaurant serves x meals of chicken quarters daily and makes soup each day using \(\frac{1}{2}\) of a chicken. The chef expresses the number of chickens she uses each 1 1 day as \(\frac{1}{4}\)x + \(\frac{1}{2}\). How many chickens does she use in three days?
Answer:
Amount of chicken used in 3 days = 9x ÷ 4. or \(\frac{9}{4}\)x
Explanation:
A restaurant serves x meals of chicken quarters daily.
makes soup each day using \(\frac{1}{2}\) of a chicken.
=> Amount of soup each day used = \(\frac{1}{2}\) × x = \(\frac{1}{2}\).
Amount of chicken used daily = \(\frac{1}{4}\)x + \(\frac{1}{2}\).
Number of days = 3.
Amount of chicken used in 3 days = Amount of chicken used daily × Number of days
= [\(\frac{1}{4}\)x + \(\frac{1}{2}\)] × 3
= LCD of 4 n 2 = 4.
= [[(1 × 1)x + (1 × 2)] ÷ 4 ] × 3
= [(1x + 2x) ÷ 4]× 3
= (3x ÷ 4) × 3
= 9x ÷ 4.
Question 26.
Mary simplified the algebraic expression \(\frac{2}{3}\)x + \(\frac{1}{4}\)x as shown below.
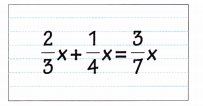
Describe and correct the error Mary made.
Answer:
Mary did not take the LCD and solved the problem, that is her error.
\(\frac{2}{3}\)x + \(\frac{1}{4}\)x = \(\frac{11}{12}\)x.
Explanation:
\(\frac{2}{3}\)x + \(\frac{1}{4}\)x
= LCD of 3 n 4 = 12.
= [(2 ×4)x + (1 × 3)x] ÷ 12
= (8x + 3x) ÷ 12
= 11x ÷ 12 or \(\frac{11}{12}\)x