Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms

by

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Lesson 3.2 Subtracting Algebraic Terms to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms

Math in Focus Grade 7 Chapter 3 Lesson 3.2 Guided Practice Answer Key

Copy and complete to simplify each expression.

Question 1.
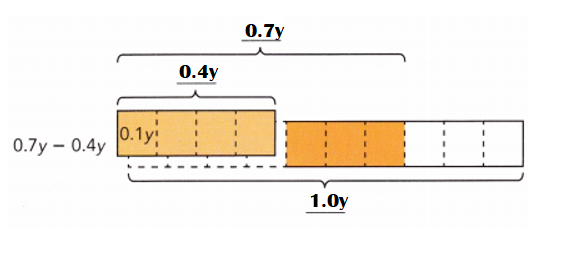
0.7y – 0.4y
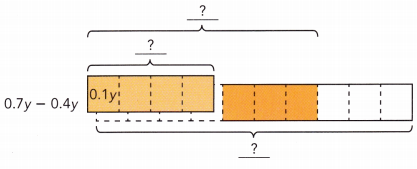
Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms 1
0.7y – 0.4y = Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms 2
Answer:
Math-in-Focus-Grade-7-Course-2-A-Chapter-3-Lesson-3.2-Answer-Key-Subtracting-Algebraic-Terms-Copy and complete to simplify each expression-1

Explanation:
0.7y – 0.4y
= 0.3y.

 

Question 2.
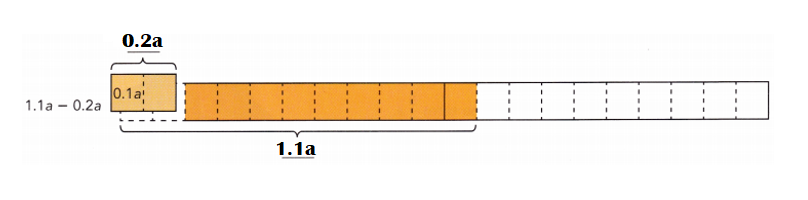
1.1a – 0.2a
Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms 3
1.1a – 0.2a = Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms 2
Answer:
Math-in-Focus-Grade-7-Course-2-A-Chapter-3-Lesson-3.2-Answer-Key-Subtracting-Algebraic-Terms-Copy and complete to simplify each expression-2

Explanation:
1.1a – 0.2a
=0.9a

 

Question 3.
1.2y – y
1.2y – y = Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms 2
Answer:
1.2y – y = 0.2y.

Explanation:
1.2y – y
= 0.2y.

 

Copy and complete to simplify each expression.
Question 4.
\(\frac{4}{9}\)x – \(\frac{1}{3}\)x
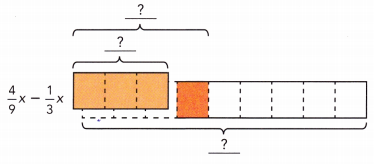
Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms 4
The LCD of \(\frac{4}{9}\) and \(\frac{1}{3}\) is Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms 2.
So, x is divided into Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms 2 x sections.
\(\frac{4}{9}\)x – \(\frac{1}{3}\)x = Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms 2
Answer:
\(\frac{4}{9}\)x – \(\frac{1}{3}\)x = \(\frac{1}{9}\)x.

Explanation:
The LCD of \(\frac{4}{9}\) and \(\frac{1}{3}\) is 9.
So, x is divided into 9  x sections.
\(\frac{4}{9}\)x – \(\frac{1}{3}\)x
= [4 – (1 × 3)]x ÷ 9
= (4 – 3)x ÷ 9
= x ÷ 9 or \(\frac{1}{9}\)x

 

Question 5.
\(\frac{3}{4}\)p – \(\frac{1}{6}\)p
\(\frac{3}{4}\)p – \(\frac{1}{6}\)p = Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms 2
= Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms 2
Rewrite the coefficients as fractions with denominator Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms 2.
Answer:
\(\frac{3}{4}\)p – \(\frac{1}{6}\)p = \(\frac{7}{12}\)p.

Explanation:
\(\frac{3}{4}\)p – \(\frac{1}{6}\)p
LCD of 4 n 6 = 12.
= [(3 × 3) – (1 × 2)]p ÷ 12
= (9 – 2)p ÷ 12
= 7p ÷ 12 or \(\frac{7}{12}\)p

Math in Focus Course 2A Practice 3.2 Answer Key

Simplify each expression with decimal coefficients.
Question 1.
0.8y – 0.7y
Answer:
0.8y – 0.7y = 0.1y.

Explanation:
0.8y – 0.7y = 0.1y.

Question 2.
0.9x – 0.6x
Answer:
0.9x – 0.6x = 0.3x.

Explanation:
0.9x – 0.6x = 0.3x.

Question 3.
1.7p – 0.4p
Answer:
1.7p – 0.4p = 1.3p.

Explanation:
1.7p – 0.4p = 1.3p.

Question 4.
1.9h – 0.9h
Answer:
1.9h – 0.9h = 1.0h.

Explanation:
1.9h – 0.9h = 1.0h.

Question 5.
1.3m – 0.5m
Answer:
1.3m – 0.5m = 0.8m.

Explanation:
1.3m – 0.5m = 0.8m.

Question 6.
1.6n – 0.8n
Answer:
1.6n – 0.8n = 0.8n.

Explanation:
1.6n – 0.8n = 0.8n.

 

Simplify each expression with fractional coefficients.
Question 7.
\(\frac{5}{6}\)x – \(\frac{1}{6}\)x
Answer:
\(\frac{5}{6}\)x – \(\frac{1}{6}\)x = \(\frac{2}{3}\)x

Explanation:
\(\frac{5}{6}\)x – \(\frac{1}{6}\)x
= (5 – 1)x ÷ 6
= 4x ÷ 6
= 2x ÷ 3 or \(\frac{2}{3}\)x

 

Question 8.
\(\frac{7}{8}\)x – \(\frac{5}{8}\)x
Answer:
\(\frac{7}{8}\)x – \(\frac{5}{8}\)x = \(\frac{1}{4}\)x.

Explanation:
\(\frac{7}{8}\)x – \(\frac{5}{8}\)x
= (7 – 5)x ÷ 8
= 2x ÷ 8
= x ÷ 4 or \(\frac{1}{4}\)x

 

Question 9.
\(\frac{9}{5}\)x – \(\frac{1}{5}\)x
Answer:
\(\frac{9}{5}\)x – \(\frac{1}{5}\)x = \(\frac{8}{5}\)x.

Explanation:
\(\frac{9}{5}\)x – \(\frac{1}{5}\)x
= (9 – 1)x ÷ 5
= 8x ÷ 5 or \(\frac{8}{5}\)x.

 

Question 10.
\(\frac{8}{3}\)p – \(\frac{1}{3}\)p
Answer:
\(\frac{8}{3}\)p – \(\frac{1}{3}\)p = \(\frac{7}{3}\)p.

Explanation:
\(\frac{8}{3}\)p – \(\frac{1}{3}\)p
= (8 – 1)p ÷ 3
= 7p ÷ 3 or \(\frac{7}{3}\)p.

 

Simplify each expression with fractional coefficients by rewriting the fractions.
Question 11.
\(\frac{1}{4}\)a – \(\frac{1}{8}\)a
Answer:
\(\frac{1}{4}\)a – \(\frac{1}{8}\)a = \(\frac{1}{8}\)a.

Explanation:
\(\frac{1}{4}\)a – \(\frac{1}{8}\)a
= LCD of 4 n 8 = 8.
= (2 – 1)a ÷ 8
= a ÷ 8 or \(\frac{1}{8}\)a

 

Question 12.
\(\frac{5}{6}\)m – \(\frac{2}{3}\)m
Answer:
\(\frac{5}{6}\)m – \(\frac{2}{3}\)m = \(\frac{1}{6}\)m

Explanation:
\(\frac{5}{6}\)m – \(\frac{2}{3}\)m
= LCD of 6 n 3 = 6.
= [5 – (2 × 2)]m ÷ 6
= (5 – 4)m ÷ 6
= m ÷ 6 or \(\frac{1}{6}\)m

 

Question 13.
\(\frac{5}{3}\)b – \(\frac{1}{6}\)b
Answer:
\(\frac{5}{3}\)b – \(\frac{1}{6}\)b = \(\frac{1}{2}\)b.

Explanation:
\(\frac{5}{3}\)b – \(\frac{1}{6}\)b
= LCD of 3 n 6 = 6.
= [(5× 2) – 1]b ÷ 6
= (10 – 1)b ÷ 6
= 9b ÷ 6
= 3b ÷ 6
= b ÷ 2 or \(\frac{1}{2}\)b.

 

Question 14.
\(\frac{7}{4}\)x – \(\frac{1}{8}\)x
Answer:
\(\frac{7}{4}\)x – \(\frac{1}{8}\)x = \(\frac{13}{8}\)x.

Explanation:
\(\frac{7}{4}\)x – \(\frac{1}{8}\)x
LCD of 4 n 8 = 8.
= [(7 × 2) – 1]x ÷ 8
= (14 – 1)x ÷ 8
= 13x ÷ 8 or \(\frac{13}{8}\)x.

 

Question 15.
\(\frac{4}{5}\)p – \(\frac{1}{3}\)p
Answer:
\(\frac{4}{5}\)p – \(\frac{1}{3}\)p = \(\frac{2}{3}\)p.

Explanation:
\(\frac{4}{5}\)p – \(\frac{1}{3}\)p
LCD of 5 n 3 = 15.
= [(4 × 3) – (1 × 5)]p ÷ 15
= (15 – 5)p ÷ 15
= 10p ÷ 15
= 2p ÷ 3 or \(\frac{2}{3}\)p.

 

Question 16.
\(\frac{3}{4}\)r – \(\frac{2}{3}\)r
Answer:
\(\frac{3}{4}\)r – \(\frac{2}{3}\)r = \(\frac{1}{12}\)r.

Explanation:
\(\frac{3}{4}\)r – \(\frac{2}{3}\)r
LCD of 4 n 3 = 12.
= [(3 × 3) – (2 × 4)]r ÷ 12
= (9 – 8)r ÷ 12
= r ÷ 12 or \(\frac{1}{12}\)r.

 

Question 17.
\(\frac{11}{7}\)k – \(\frac{1}{2}\)k
Answer:
\(\frac{11}{7}\)k – \(\frac{1}{2}\)k = \(\frac{15}{14}\)k.

Explanation:
\(\frac{11}{7}\)k – \(\frac{1}{2}\)k
LCD of 7 n 2 = 14.
= [(11 × 2) – (1 × 7)]k ÷ 14
= (22 – 7)k ÷ 14
= 15k ÷ 14 or \(\frac{15}{14}\)k.

 

Question 18.
\(\frac{7}{4}\)d – \(\frac{3}{5}\)d
Answer:
\(\frac{7}{4}\)d – \(\frac{3}{5}\)d = \(\frac{23}{20}\)d.

Explanation:
\(\frac{7}{4}\)d – \(\frac{3}{5}\)d
LCD of 4 n 5 = 20.
= [(7 × 5) – (3 × 4)]d ÷ 20
= (35 – 12)d ÷ 20
= 23d ÷ 20 or \(\frac{23}{20}\)d.

 

Solve. Show your work.
Question 19.
Math Journal Matthew simplified the algebraic expression \(\frac{3}{2}\)x – \(\frac{1}{3}\)x as shown below.
\(\frac{3}{2}\)x – \(\frac{1}{4}\)x = \(\frac{18}{12}\)x – \(\frac{4}{12}\)x
= \(\frac{14}{12}\)x
Is Matthew’s simplification correct? Why or why not?
Answer:
Matthew’s simplification is incorrect because \(\frac{3}{2}\)x – \(\frac{1}{4}\)x  is not equal to \(\frac{18}{12}\)x – \(\frac{4}{12}\)x.

Explanation:
\(\frac{3}{2}\)x – \(\frac{1}{4}\)x
LCD of 2 n 4 = 4.
= [(3 × 2) – (1 × 1)]x ÷ 4
= (6 – 1)x ÷ 4
= 5x ÷ 4 or \(\frac{5}{4}\)x.

\(\frac{18}{12}\)x – \(\frac{4}{12}\)x
= (18 – 4)x ÷ 12
= 14x ÷ 12
= 7x ÷ 6 or \(\frac{7}{6}\)x.

\(\frac{14}{12}\)x = \(\frac{7}{6}\)x

 

Question 20.
Rectangle A, shown below, is larger than rectangle B. Write and simplify an algebraic expression that represents the difference in the areas of the two rectangles.
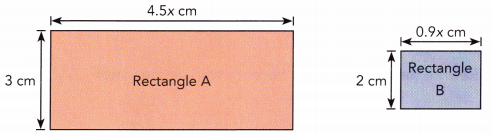
Math in Focus Grade 7 Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms 5
Answer:
Difference in the Area of rectangle A and Area of rectangle B = 11.7 square cm.

Explanation:
Area of rectangle A = Length × Width
= 4.5cm  × 3cm
= 13.5 square cm.
Area of rectangle B = Length × Width
= 0.9cm  × 2cm
= 1.8 square cm.
Difference in the Area of rectangle A and Area of rectangle B:
= 13.5 square cm – 1.8 square cm
= 11.7 square cm.

Leave a Comment