Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Lesson 3.3 Simplifying Algebraic Expressions to finish your assignments.
Math in Focus Grade 7 Course 2 A Chapter 3 Lesson 3.3 Answer Key Simplifying Algebraic Expressions
Math in Focus Grade 7 Chapter 3 Lesson 3.3 Guided Practice Answer Key
Complete.
Question 1.
1.5t + 4t+ 3
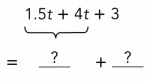
Answer:
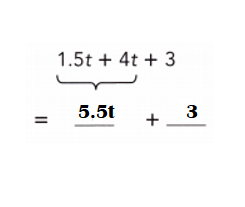
Explanation:
1.5t + 4t+ 3
= 5.5t + 3.
Question 2.
1.8m – 0.9m + 2
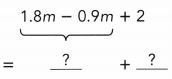
Answer:
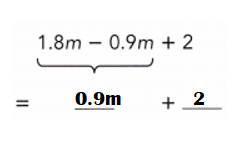
Explanation:
1.8m – 0.9m + 2
= 0.9m + 2.
Copy and complete to simplify each expression.
Question 3.
\(\frac{2}{3}\)x – \(\frac{1}{6}\)x + 1 + 6
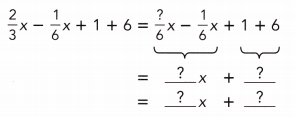
Answer:
\(\frac{2}{3}\)x – \(\frac{1}{6}\)x + 1 + 6 = \(\frac{1}{2}\)x + 7.
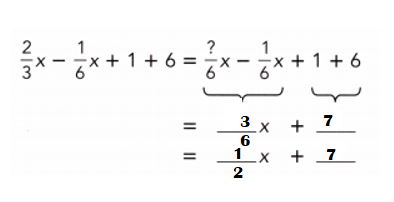
Explanation:
\(\frac{2}{3}\)x – \(\frac{1}{6}\)x + 1 + 6
= \(\frac{2}{3}\)x – \(\frac{1}{6}\)x + 7
LCD of 3 n 6 = 6.
= [(2 × 2)x – (1 × 1)x] ÷ 6 + 7
= (4x – x) ÷ 6 + 7
= 3x ÷ 6 + 7
= x ÷ 2 + 7.
Question 4.
\(\frac{1}{3}\)d + \(\frac{7}{12}\)d – 5 – 1
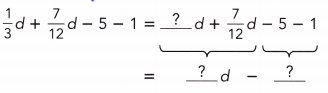
Answer:
\(\frac{1}{3}\)d + \(\frac{7}{12}\)d – 5 – 1 = \(\frac{11}{12}\)d – 4.
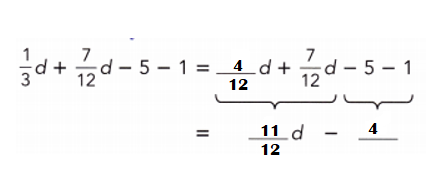
Explanation:
\(\frac{1}{3}\)d + \(\frac{7}{12}\)d – 5 – 1
= \(\frac{1}{3}\)d + \(\frac{7}{12}\)d – 4
LCD of 3 n 12 = 12.
= [(1 × 4)d + (7 × 1)d] ÷ 12 – 4
= (4d + 7d) ÷ 12 – 4
= 11d ÷ 12 – 4 or \(\frac{11}{12}\)d – 4.
Question 5.
\(\frac{1}{2}\)k – \(\frac{2}{5}\)k + 8 – 3
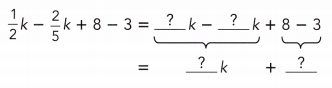
Answer:
\(\frac{1}{2}\)k – \(\frac{2}{5}\)k + 8 – 3 = \(\frac{1}{10}\)k + 5.
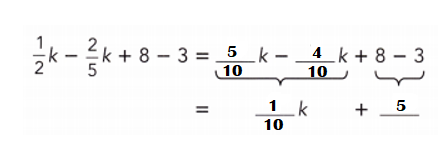
Explanation:
\(\frac{1}{2}\)k – \(\frac{2}{5}\)k + 8 – 3
= \(\frac{1}{2}\)k – \(\frac{2}{5}\)k + 5
LCD of 2 n 5 = 10.
= [(1 × 5)k – (2 × 2) k] ÷ 10 + 5
= (5k – 4k) ÷ 10 + 5
= k ÷ 10 + 5 or \(\frac{1}{10}\)k + 5.
Copy and complete to simplify each expression.
Question 6.
0.5k + 0.3k + 1.2k
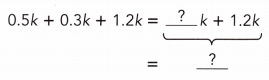
Answer:
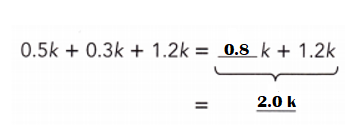
Explanation:
0.5k + 0.3k + 1.2k
= 0.8k + 1.2k
= 2.0k.
Question 7.
\(\frac{1}{2}\)p + \(\frac{1}{2}\)p – \(\frac{1}{2}\)p
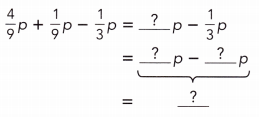
Answer:
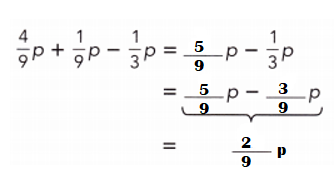
Explanation:
\(\frac{1}{2}\)p + \(\frac{1}{2}\)p – \(\frac{1}{2}\)p
= (1 + 1)p ÷ 2 – \(\frac{1}{2}\)p
= 2p ÷ 2 – \(\frac{1}{2}\)p
= p ÷ 1 – \(\frac{1}{2}\)p
= (2p – p) ÷ 2
= p ÷ 2 or – \(\frac{1}{2}\)p.
Complete to simplify each expression.
Question 8.
4a + 5 + a + 7
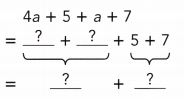
Answer:
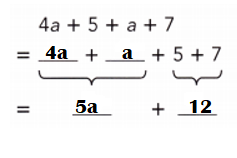
Explanation:
4a + 5 + a + 7
= 4a + a + 7 + 5
= 5a + 7 + 5
= 5a + 12.
Question 9.
\(\frac{3}{7}\)x + \(\frac{3}{5}\) – \(\frac{2}{7}\)x – \(\frac{2}{5}\)
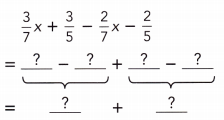
Answer:
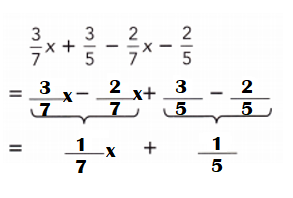
Explanation:
\(\frac{3}{7}\)x + \(\frac{3}{5}\) – \(\frac{2}{7}\)x – \(\frac{2}{5}\)
= \(\frac{3}{7}\)x – \(\frac{2}{7}\)x + \(\frac{3}{5}\) – \(\frac{2}{5}\)
= [(3 – 2)x ÷ 7] + \(\frac{3}{5}\) – \(\frac{2}{5}\)
= \(\frac{1}{7}\)x + \(\frac{3}{5}\) – \(\frac{2}{5}\)
= \(\frac{1}{7}\)x + [(3 – 2) ÷ 5]
= \(\frac{1}{7}\)x + \(\frac{1}{5}\).
Copy and complete to simplify each expression.
Question 10.
6a + 9b + a + b
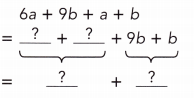
Answer:
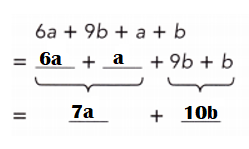
Explanation:
6a + 9b + a + b
= 6a + a + 9b + b
= 7a + 9b + b
= 7a + 10b.
Question 11.
3x + 2y – 2x – 3y
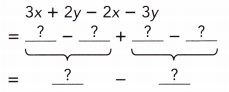
Answer:
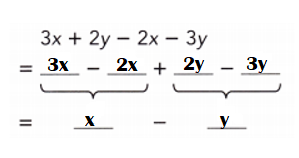
Explanation:
3x + 2y – 2x – 3y
= 3x – 2x – 3y + 2y
= x – 3y + 2y
= x – y.
Math in Focus Course 2A Practice 3.3 Answer Key
Simplify each expression with one variable.
Question 1.
0.3x + 0.6x + 3
Answer:
0.3x + 0.6x + 3 = 0.9x + 3.
Explanation:
0.3x + 0.6x + 3
= 0.9x + 3.
Question 2.
\(\frac{2}{7}\)x + \(\frac{3}{7}\)x + 4
Answer:
\(\frac{2}{7}\)x + \(\frac{3}{7}\)x + 4 = \(\frac{5}{7}\)x + 4.
Explanation:
\(\frac{2}{7}\)x + \(\frac{3}{7}\)x + 4
= (2 + 3)x ÷ 7 + 4
= 5x ÷ 7 + 4
= \(\frac{5}{7}\)x + 4.
Question 3.
0.8x – 0.2x – 5
Answer:
0.8x – 0.2x – 5 = 0.6x – 5.
Explanation:
0.8x – 0.2x – 5
= 0.6x – 5.
Question 4.
\(\frac{7}{8}\)x – \(\frac{1}{8}\)x – 5
Answer:
\(\frac{7}{8}\)x – \(\frac{1}{8}\)x – 5 = \(\frac{3}{4}\)x – 5.
Explanation:
\(\frac{7}{8}\)x – \(\frac{1}{8}\)x – 5
= (7 – 1)x ÷ 8 – 5
= 6x ÷ 8 – 5
= 3x ÷ 4 – 5 or \(\frac{3}{4}\)x – 5.
Simplify each expression with three algebraic terms.
Question 5.
0.3p + 0.2p + 0.4p
Answer:
0.3p + 0.2p + 0.4p = 0.9p.
Explanation:
0.3p + 0.2p + 0.4p
= 0.5p + 0.4p
= 0.9p.
Question 6.
0.2 + o.8p – 0.6p
Answer:
0.2 + o.8p – 0.6p = 0.2(1 + p).
Explanation:
0.2 + o.8p – 0.6p
= 0.2 + 0.2p.
= 0.2(1 + p).
Question 7.
\(\frac{1}{3}\)y + \(\frac{1}{6}\)y + \(\frac{5}{12}\)y
Answer:
\(\frac{1}{3}\)y + \(\frac{1}{6}\)y + \(\frac{5}{12}\)y = \(\frac{2}{3}\)y.
Explanation:
\(\frac{1}{3}\)y + \(\frac{1}{6}\)y + \(\frac{5}{12}\)y
= LCD of 3 n 6 = 6.
= [(2 + 1)y ÷ 6] + \(\frac{5}{12}\)y
= 3y ÷ 6 + \(\frac{5}{12}\)y
= y ÷ 6 + \(\frac{5}{12}\)y
= \(\frac{1}{6}\)y + \(\frac{5}{12}\)y
LCD of 6 n 12 = 12.
= [(1 × 2) + 5]y ÷ 12
= (3 + 5)y ÷ 12
= 8y ÷ 12
= 2y ÷ 3 or \(\frac{2}{3}\)y.
Question 8.
\(\frac{1}{2}\)a + \(\frac{2}{3}\)a – \(\frac{1}{6}\)a
Answer:
\(\frac{1}{2}\)a + \(\frac{2}{3}\)a – \(\frac{1}{6}\)a = a.
Explanation:
\(\frac{1}{2}\)a + \(\frac{2}{3}\)a – \(\frac{1}{6}\)a
= LCD of 2 n 3 = 6.
= [(1 × 3) + (2 × 2)]a ÷ 6 – \(\frac{1}{6}\)a
= (3 + 4)a ÷ 6 – \(\frac{1}{6}\)a
= \(\frac{7}{6}\)a – \(\frac{1}{6}\)a
= (7 – 1)a ÷ 6
= 6a ÷ 6
= a ÷ 1 or a.
Simplify each expression with one variable.
Question 9.
7x + 6 + 4x
Answer:
7x + 6 + 4x = 11x + 6.
Explanation:
7x + 6 + 4x
= 7x + 4x + 6
= 11x + 6.
Question 10.
8y – 4 – 6y
Answer:
8y – 4 – 6y = 2y – 4.
Explanation:
8y – 4 – 6y
= 8y – 6y – 4
= 2y – 4.
Question 11.
1.8x – 0.6 – 0.7x
Answer:
1.8x – 0.6 – 0.7x = 1.1x – 0.6.
Explanation:
1.8x – 0.6 – 0.7x
= 1.8x – 0.7x – 0.6
= 1.1x – 0.6.
Question 12.
\(\frac{4}{7}\)x + \(\frac{1}{5}\) + \(\frac{2}{7}\)x
Answer:
\(\frac{4}{7}\)x + \(\frac{1}{5}\) + \(\frac{2}{7}\)x = \(\frac{6}{7}\)x + \(\frac{1}{5}\).
Explanation:
\(\frac{4}{7}\)x + \(\frac{1}{5}\) + \(\frac{2}{7}\)x
= \(\frac{4}{7}\)x + \(\frac{2}{7}\)x + \(\frac{1}{5}\)
= (4 + 2)x ÷ 7 + \(\frac{1}{5}\)
= 6x ÷ 7 + \(\frac{1}{5}\)
= \(\frac{6}{7}\)x + \(\frac{1}{5}\)
Simplify each expression with two variables.
Question 13.
2x + 4x + 7y
Answer:
2x + 4x + 7y = 6x + 7y.
Explanation:
2x + 4x + 7y
= 6x + 7y.
Question 14.
5x + x + 3y
Answer:
5x + x + 3y = 6x + 3y.
Explanation:
5x + x + 3y
= 6x + 3y.
Question 15.
9x + 7x + 3y
Answer:
9x + 7x + 3y = 16x + 3y.
Explanation:
9x + 7x + 3y
= 16x + 3y.
Question 16.
8m – 7m – 6n
Answer:
8m – 7m – 6n = m – 6n.
Explanation:
8m – 7m – 6n
= m – 6n.
Question 17.
2.3a – 1.8a + 3.5b – 2.7b
Answer:
2.3a – 1.8a + 3.5b – 2.7b = 0.5a + 0.8b.
Explanation:
2.3a – 1.8a + 3.5b – 2.7b
= 0.5a + 3.5b – 2.7b
= 0.5a + 0.8b.
Question 18.
2.5x + 1.8z + 1.6x + 0.9z
Answer:
2.5x + 1.8z + 1.6x + 0.9z = 4.1x + 2.7z.
Explanation:
2.5x + 1.8z + 1.6x + 0.9z
= 2.5x + 1.6x + 1.8z + 0.9z
= 4.1x + 2.7z.
Question 19.
\(\frac{3}{5}\)a + \(\frac{2}{5}\)a + \(\frac{1}{6}\)b + \(\frac{1}{6}\)b
Answer:
\(\frac{3}{5}\)a + \(\frac{2}{5}\)a + \(\frac{1}{6}\)b + \(\frac{1}{6}\)b = a + \(\frac{1}{3}\)b.
Explanation:
\(\frac{3}{5}\)a + \(\frac{2}{5}\)a + \(\frac{1}{6}\)b + \(\frac{1}{6}\)b
= [(3 + 2)a ÷ 5] + \(\frac{1}{6}\)b + \(\frac{1}{6}\)b
= [5a ÷ 5] + \(\frac{1}{6}\)b + \(\frac{1}{6}\)b
= a + \(\frac{1}{6}\)b + \(\frac{1}{6}\)b
= a + [(1 + 1)b ÷ 6]
= a + [2b ÷ 6]
= a + \(\frac{1}{3}\)b.
Question 20.
\(\frac{2}{3}\)a – \(\frac{1}{6}\)a + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b
Answer:
\(\frac{2}{3}\)a – \(\frac{1}{6}\)a + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b = \(\frac{1}{2}\)a + \(\frac{3}{10}\)b.
Explanation:
\(\frac{2}{3}\)a – \(\frac{1}{6}\)a + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b
LCD of 3 n 6 = 6.
= [[(2 × 2) – (1 × 1)]a ÷ 6] + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b
= [(4 – 1)a ÷ 6] + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b
= (3a ÷ 6) + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b
= \(\frac{1}{2}\)a + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b
LCD of 5 n 10 = 10.
= \(\frac{1}{2}\)a + [[(3 × 2) – (3 × 1)]b ÷ 10]
= \(\frac{1}{2}\)a + [(6 – 3)b ÷ 10]
= \(\frac{1}{2}\)a + (3b ÷ 10)
= \(\frac{1}{2}\)a + \(\frac{3}{10}\)b.
Find the perimeter of each figure.
Question 21.
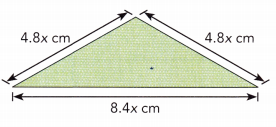
Answer:
Perimeter of triangle = 18cm.
Explanation:
Perimeter of triangle = Side + side + side
= 4.8cm + 4.8cm + 8.4cm
= 9.6cm + 8.4cm
= 18cm.
Question 22.
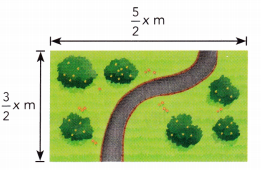
Answer:
Perimeter of rectangle = 8m.
Explanation:
Perimeter of rectangle = 2(Length + Width)
= 2( \(\frac{5}{2}\)m + \(\frac{3}{2}\)m)
= 2[(5 + 3)÷2]m
= 2 (8 ÷ 2)m
= 2 × 4m
= 8m.
Question 23.
Math journal When adding or subtracting algebraic expressions, how do you identify the like terms?
Answer:
We identity the like terms if they have the same variable (or variables) with the same exponent and later do the addition or subtraction process required to solve the problem.
Explanation:
Two or more like terms are like if they have the same variable (or variables) with the same exponent. To combine like terms, we add or subtract the coefficients. The variable factors remain the same.