This handy Math in Focus Grade 7 Workbook Answer Key Chapter 10 Lesson 10.1 Defining Outcomes, Events, and Sample Space detailed solutions for the textbook questions.
Math in Focus Grade 7 Course 2 B Chapter 10 Lesson 10.1 Answer Key Defining Outcomes, Events, and Sample Space
Hands-On Activity
Materials:
- paper
- scissors
Work in pairs.
Step 1: Make a set of four small cards with the following digits written on them.
![]()
Step 2: Pick three cards and form a 3-digit number. Record the number.
Step 3: Find all the possible 3-digit numbers that you can form. The list of numbers represents all the possible outcomes for the activity.
Step 4: Tell how many outcomes are in the sample space for this activity.
Math in Focus Grade 7 Chapter 10 Lesson 10.1 Guided Practice Answer Key
Solve.
Question 1.
Select a letter from the list of letters: A, D, E, G, K.
a) List all the possible outcomes.
Answer:
I selected the letter A. From this, we can write the possible outcomes.
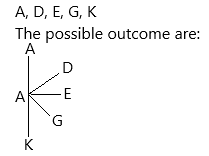
The possible outcomes are: AA, AD, AE, AG, AK
If we select letter D, then the possible outcomes are:
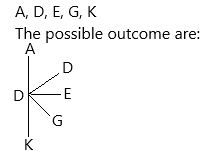
The possible outcomes are: AD, DD, DE, DG, DK
If we take letter E, then the possible outcomes are:
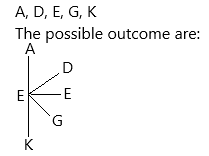
The possible outcomes are: EA, Ed, EE, EG, EK
Likewise, take letter G:
The possible outcomes are: GA, GD, GE, GG, GK
Take letter K:
The possible outcomes are: KA, KD, KE, KG, KK
b) State the number of outcomes in the sample space.
Answer:
The above possible outcomes are called sample space.
A sample space is a collection of a set of possible outcomes of a random experiment. The sample space is represented using the symbol, “S”. The subset of possible outcomes of an experiment is called events. A sample space may contain a number of outcomes that depends on the experiment. If it contains a finite number of outcomes, then it is known as discrete or finite sample spaces.
The samples spaces for a random experiment is written within curly braces “ { } “. There is a difference between the sample space and the events. For rolling a die, we will get the sample space, S as {1, 2, 3, 4, 5, 6 } whereas the event can be written as {1, 3, 5 } which represents the set of odd numbers and { 2, 4, 6 } which represents the set of even numbers. The outcomes of an experiment are random and the sample space becomes the universal set for some particular experiments.
sample space A={AA, AD, AE, AG, AK}
sample space D={AD, DD, DE, DG, DK}
sample space E={EA, Ed, EE, EG, EK}
sample space G={GA, GD, GE, GG, GK}
sample space K={KA, KD, KE, KG, KK}
Each letter has 5 sample points. Likewise, 5 letters are there. So the total number of outcomes in the sample space are 5*5=25.
Therefore, there are 25 outcomes in the sample space.
Question 2.
Use the letter cards below to form all possible 3-letter English words.

a) List all the possible outcomes.
Answer:
The calculating of possible outcomes is a process for determining the number of possible results for an event. There are various methods for conducting this process. The best way to calculate the number of possible outcomes of an event is dependent on the type of event and the structure of the event.
By using the above-given letters a b c d d
The possible three-letter English words are:
add, bad, cab, cad, dab, dad
b) State the number of outcomes in the sample space.
Answer:
The above possible outcomes are called sample space.
A sample space is a collection of a set of possible outcomes of a random experiment. The sample space is represented using the symbol, “S”. The subset of possible outcomes of an experiment is called events. A sample space may contain a number of outcomes that depends on the experiment. If it contains a finite number of outcomes, then it is known as discrete or finite sample spaces.
The samples spaces for a random experiment is written within curly braces “ { } “. There is a difference between the sample space and the events. For rolling a die, we will get the sample space, S as {1, 2, 3, 4, 5, 6 } whereas the event can be written as {1, 3, 5 } which represents the set of odd numbers and { 2, 4, 6 } which represents the set of even numbers. The outcomes of an experiment are random and the sample space becomes the universal set for some particular experiments.
sample space a={add}
sample space b={bad}
sample space c={cab, cad}
sample space d={dab}
sample space d={dad}
Therefore, 6 outcomes in the sample space
Question 3.
Y is the event of choosing a prime number from a list of whole numbers from 1 to 20.
a) List the outcomes favorable to event Y.
The prime numbers up to 20 are ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Y = {![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() }
}
Answer:
Prime numbers from 1 to 20 are the numbers that have exactly two factors and are not divisible further into a product of two natural numbers other than 1 and itself. To find whether ‘x’ is a prime number from 1 to 20, we need to check the below-mentioned conditions (all three at the same time):
Prime numbers 1 to 20 condition 1: Number should be divisible by 1 (x ÷ 1 = x)
Prime numbers 1 to 20 condition 2: Number should be divisible by itself. (x ÷ x =1)
prime numbers 1to 20 condition 3: Number must have only 2 factors 1 and the same number.
If event Y= prime numbers
You can get 2, 3, 5, 7, 11, 13, 17, 19.
b) State the number of outcomes in the sample space.
You choose from ![]() outcomes. There are
outcomes. There are ![]() outcomes in the sample space.
outcomes in the sample space.
Answer:20; 20
The above possible outcomes are called sample space.
A sample space is a collection of a set of possible outcomes of a random experiment. The sample space is represented using the symbol, “S”. The subset of possible outcomes of an experiment is called events. A sample space may contain a number of outcomes that depends on the experiment. If it contains a finite number of outcomes, then it is known as discrete or finite sample spaces.
Sample space={2, 3, 5, 7, 11, 13, 17, 19}
Therefore, there are 20 outcomes in the sample space.
Question 4.
You choose a shape from a bag containing these cardboard geometric shapes.
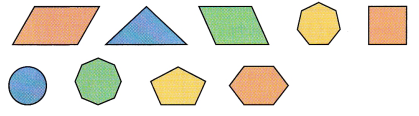
a) List all the favorable outcomes for the event of choosing a shape with at most 6 sides.
Answer:
Brown parallelogram, triangle, green parallelogram, square, pentagon, and hexagon.
Explanation:
Triangle: Triangle is a polygon, which is made of three sides and consists of three edges and three vertices. Also, the sum of its internal angles equals 180o.
Square: Square is a quadrilateral where all the four sides and angles are equal and the angles at all the vertices equal to 90° each.
Parallelogram: A parallelogram is a quadrilateral with two pairs of parallel sides and opposite angles are equal in measures.
Pentagon: Pentagons can be simple or self-intersection. The properties of a simple pentagon (5-gon) are it must have five straight sides that meet to create five vertices, but do not self-intersect: Pentagons have five straight sides. Pentagons have five interior angles, which sum to 540° 540 °. The five sides do not intersect.
Hexagon: The hexagon is made up of 6 regular triangles. A closed figure which is two-dimensional and is made up of straight lines is called a polygon. A polygon is a geometric figure. In this type of geometric figures, if one has 6 sides, it is called a Hexagon.
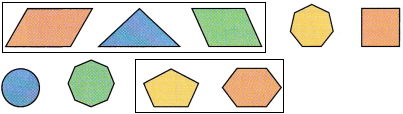
b) List all the favorable outcomes for the event of choosing a shape with more than 4 angles.
Answer: Heptagon, octagon, pentagon, hexagon
Explanation:
Pentagon: Pentagons can be simple or self-intersection. The properties of a simple pentagon (5-gon) are it must have five straight sides that meet to create five vertices, but do not self-intersect: Pentagons have five straight sides. Pentagons have five interior angles, which sum to 540° 540 °. The five sides do not intersect.
Hexagon: The hexagon is made up of 6 regular triangles. A closed figure which is two-dimensional and is made up of straight lines is called a polygon. A polygon is a geometric figure. In this type of geometric figures, if one has 6 sides, it is called a Hexagon.
Heptagon: A heptagon has 7 sides, 7 edges, and 7 vertices. The sum of the interior angles of a heptagon is equal to 900°. The value of each interior angle of a regular heptagon is equal to 128.57°.
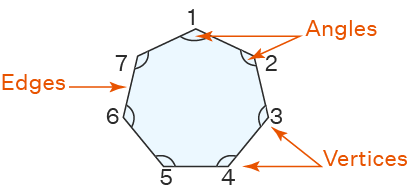
Octagon:
In the case of properties, we usually consider regular octagons.
– These have eight sides and eight angles.
– All the sides and all the angles are equal, respectively.
– There are a total of 20 diagonals in a regular octagon.
– The total sum of the interior angles is 1080°, where each angle is equal to 135°(135×8 = 1080)
– The Sum of all the exterior angles of the octagon is 360°, and each angle is 45°(45×8=360).
Math in Focus Course 2B Practice 10.1 Answer Key
Solve.
Question 1.
A bag contains 2 red balls and 1 green ball. A ball is taken out from the bag. What are the types of outcomes?
Answer:
The types of outcomes are red and green and we can find probability also.
Explanation:
The number of red balls=2
The number of green balls=1
The total number of balls=2+1=3
If one ball is drawn from the bag then the possible outcomes are:
P (A) = n (E)/n (S)
Where P (A) is the probability of an event “A”.
n (E) is the number of favourable outcomes.
n (S) is the total number of events in the sample space

The number of outcomes for the red ball is 1
The number of outcomes for other red ball=1
The number of outcomes for green ball=1
The total number of outcomes=1+1+1=3
P (A) = n (E)/n (S)
P (A) = 1/3.
Question 2.
A number die with faces numbered 1 to 6 is rolled once. What are the favorable outcomes for the event of getting a value that is evenly divisible by 3?
Answer:
Explanation:
– The sample space is the list of all possible outcomes.
– A dice has 6 sides which are all equally likely to be rolled.
– Each side has a different number written on it.
– we can roll a: 1, 2, 3, 4, 5, 6
– we say that the sample space for dice is {1, 2, 3, 4, 5, 6}
– The numbers that are divisible by 3 are 3 and 6.
– Therefore, the possible outcomes are {3, 6}.
Question 3.
A spinner has 5 values, as shown in the diagram. You spin the spinner and record where the spinner lands.
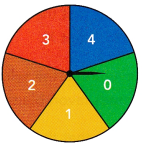
a) List all the outcomes in the sample space.
Answer:
The above possible outcomes are called sample space.
A sample space is a collection of a set of possible outcomes of a random experiment. The sample space is represented using the symbol, “S”. The subset of possible outcomes of an experiment is called events. A sample space may contain a number of outcomes that depends on the experiment. If it contains a finite number of outcomes, then it is known as discrete or finite sample spaces.
Sample space={0, 1, 2, 3, 4}
– This spinner is split into 5 equal sections.
– One section contains 0 and another section contains 1, 2, 3, 4
– If we take 0 in one spin then the possible outcome of 0 is 1/5.
– If we take 1 in one spin then the possible outcome of 1 is 1/5.
– If we take 2 in one spin then the possible outcome of 2 is 1/5.
– If we take 3 in one spin then the possible outcome of 3 is 1/5.
– If we take 4 in one spin then the possible outcome of 4 is 1/5.
b) If event A is the event of landing on an even number, what are the outcomes favorable to event A?
Answer:
The samples spaces for a random experiment is written within curly braces “ { } “. There is a difference between the sample space and the events. For rolling a die, we will get the sample space, S as {1, 2, 3, 4, 5, 6 } whereas the event can be written as {1, 3, 5 } which represents the set of odd numbers and { 2, 4, 6 } which represents the set of even numbers. The outcomes of an experiment are random and the sample space becomes the universal set for some particular experiments.
Sample space={0, 1, 2, 3, 4}
– This spinner is split into 5 equal sections.
In the sample space, the even numbers are 0,2, and 4.
Event A={0, 2, 4}
Total number of outcomes = n(S) = 5
A be the event of landing on even numbers
Number of favourable outcomes for each even number= n(A) = 1
that is for each even number 0, 2, 4
Question 4.
A basketball coach has 5 forwards, 2 centers, and 5 guards. E is the event of the coach picking a forward to be the team captain. How many outcomes are favorable to event E?
Answer: 5 outcomes
Explanation:
the above-given question:
The number of forwards a basketball coach has=5
The number of centres=2
The number of guards=5
The event of coach picking forwards to be the team captain=E
The number of favourable outcomes to event E=N (E).
N (E)= 5
Here asked only forwards. Therefore, 5 forwards are given so 5 possible outcomes will come.
Question 5.
A letter is selected from the letters in the name TYRANNOSAURUS REX. What is the number of possible outcomes?
Answer: 16
Explanation:
![]()
We are selecting the letters one by one.
In the word, TYRANNOSAURUS REX has 16 letters.
Therefore, the possibility of outcomes is 16.
Question 6.
A colored disk is drawn from a bag which contains the following disks.

a) If you record only the color of the disk, what are the types of outcomes?
Answer: orange, green, blue
Explanation:
If we select the disk to be drawn from a bag and the disks are having only three colours. Those three colours are orange, green, blue. Anytime you draw a disk definitely we will get those three colours.
b) If you record only the letter on the disk, what are the types of outcomes?
Answer: A, D, J, G, F, K
Explanation:
These are the possible outcomes because in the disks those letters are written.
And there is a possibility of getting 2A’s 2D’s 2K’s 1J 1G 1F.
c) If you record both the colour and the letter of the disk, what are the types of outcomes?
Answer:
If we record both colour and letter then the outcomes will be:
Orange colour with letters A, A, F, D
Green colour with letters D, K
Blue colour with letters J, G, K
Question 7.
There are 10 multiple-choice questions in a test. A student gets 1 point for every correct answer and 0 points for every wrong answer. No point is awarded for a question that the student does not try to answer.
a) What is the highest score a student could receive on the test?
Answer: 10
Explanation:
The above-given question:
The number of multiple-choice questions=10
The number of points students will get to each correct answer=10
The number of points students will get to each wrong answer=0
The highest score the students could receive on the test=X
for 10 correct answers=10 marks
for 9 correct answers=9 marks
for 8 correct answers=8 marks and so on…
compare to all the marks 10 is the highest mark.
Therefore, 10 marks will be the highest score.
b) What is the lowest possible score a student could receive?
Answer: 0
Explanation:
The number of multiple-choice questions=10
The number of points students will get to each correct answer=10
The number of points students will get to each wrong answer=0
The highest score the students could receive on the test=X
for 10 correct answers=10 marks
for 9 correct answers=9 marks
for 8 correct answers=8 marks
for 7 correct answers=7 marks
for 6 correct answers=6 marks
for 5 correct answers=5 marks
for 4 correct answers=4 marks
for 3 correct answers=3 marks
for 2 correct answers=2 marks
for 1 correct answer=1 mark
for 0 correct answers=0 marks
Compared to all the marks 0 is the lowest mark.
Therefore, 0 is the lowest mark.
c) What are the possible outcomes for a score on the multiple choice test?
Answer: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
The number of multiple-choice questions=10
The number of points students will get to each correct answer=10
The number of points students will get to each wrong answer=0
The highest score the students could receive on the test=X
for 10 correct answers=10 marks
for 9 correct answers=9 marks
for 8 correct answers=8 marks
for 7 correct answers=7 marks
for 6 correct answers=6 marks
for 5 correct answers=5 marks
for 4 correct answers=4 marks
for 3 correct answers=3 marks
for 2 correct answers=2 marks
for 1 correct answer=1 mark
for 0 correct answers=0 marks
These are all the possible outcomes to a student getting a score on the multiple-choice test.
Question 8.
A student is to be selected to play a supporting role in a drama from the list of names below.
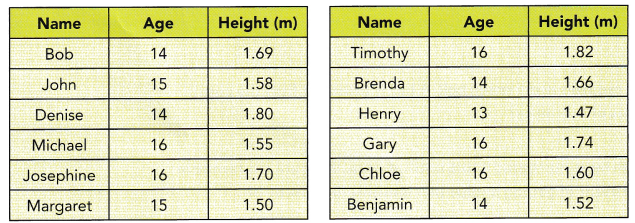
a) X is the event that the selected student is 14 years old. List the outcomes favourable to event X.
Answer: Bob, Denise, Brenda, Benjamin
Explanation:
The above-given question:
Certain names, ages, and heights are given.
n (X) = number of possible outcomes to event X.
Once, look at the above chart and observe the age who are having 14 years. Those students are all the possible outcomes to event X.
n (X)={Bob, Denise, Brenda, Benjamin}
therefore, the number of outcomes is 4.
b) Y is the event that the selected student is at least 1.56 meters tall. List all the outcomes favorable to event Y.
Answer:
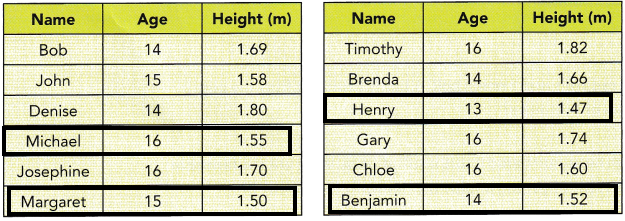
Explanation:
Once, look at the above chart and observe the height who are having at least 1.56 metres. Those students are all the possible outcomes to event Y.
n (Y)=number of possible outcomes to event Y.
n (y)={Michael, Margaret, Henry, Benjamin}
therefore, the number of outcomes is 4.
c) Z is the event that the selected student is at least 1.7 meters tall and at least 15 years old. How many outcomes are favorable to this event?
Answer:
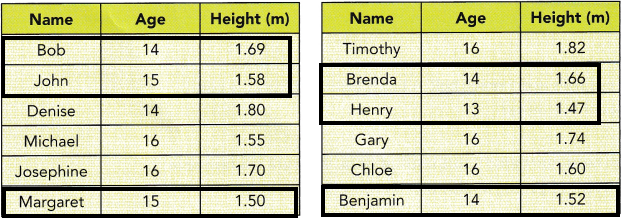
Explanation:
Once, look at the above chart and observe the height and age who are having at least 1.7 metres and 15 years old. Those students are all the possible outcomes to event Z.
At least means we can select 1.7 and below 1.7 and coming to the age at least 15 years means we can select 15 and below 15 years old.
n (Z)=number of possible outcomes to event Z.
n (Z)={Bob, John, Margaret, Brenda, Henry, Benjamin}
therefore, the number of outcomes is 6.
d) W is the event that the name of the selected student has at most 5 letters. What outcomes are favorable to event W?
Answer:
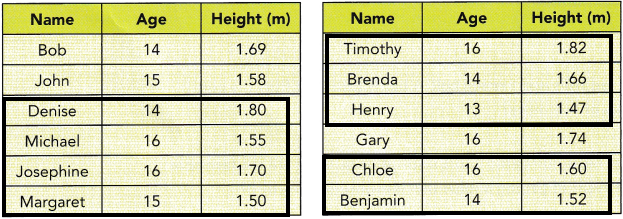
Once, look at the above chart and observe the names column who are having at most 5 letters. Those students are all the possible outcomes to event W.
At most means, we can select 5 letters or more than 5 letters
n (W)= the number of possible outcomes to event W.
n (Z)={Denise, Michael, Josephine, Margaret, Timothy, Brenda, Henry, Chole, Benjamin}
therefore, the number of outcomes is 9.
Question 9.
From the list of digits, 0, 5, 7, 8, you form a 3-digit number without any repeating digits. You do not include any numbers that start with 0.
a) List all the outcomes of the sample space.
Answer:
Sample space= { 507, 508, 570, 578, 580, 587, 705, 708, 750, 758, 780, 785, 805, 807, 850, 857, 870, 875}
These are the outcomes of the 3-digit numbers not starting with the number 0.
b) List all the favorable outcomes for the event that a 3-digit number is an even number.
Answer:
Let’s assume that the event is A.
Event A is the even number which should be a 3-digit number.
Even number: Even numbers are those numbers that can be divided into two equal groups or pairs and are exactly divisible by 2.
Event A= {508, 570, 578, 580, 708, 750, 758, 780, 850, 870}
c) List all the favorable outcomes for the event that the 3-digit number is an odd number.
Answer:
Let’s assume that the event is B.
Event B is the odd number which should be a 3-digit number.
Odd numbers are the numbers that cannot be divided by 2 evenly. It cannot be divided into two separate integers evenly. If we divide an odd number by 2, then it will leave a remainder. The examples of odd numbers are 1, 3, 5, 7, etc.
Event B= {507, 587, 705, 785, 805, 807, 857, 875}
Question 10.
You pick a whole number between 1 and 100. If A is the event that the number you picked is divisible by 3 and 7, what are the outcomes favourable to event A?
Answer:
If event A=numbers are divisible by 3
you can get 3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60 63 66 69 72 75 78 81 84 87 90 93 96 99
n (A)=33
P (A)=33/100
If event A=numbers are divisible by 7
you can get 7 14 21 28 35 42 49 56 63 70 77 84 91 98
n (A)=14
p (A)=14/100
The Single Event Probability Calculator uses the following formulas: P (E) = n (E) / n (T) = (number of outcomes in the event) / (total number of possible outcomes) n (T) is the total number of possible outcomes. n (T) is the total number of possible outcomes.
P (E)= n (E) / n (T)
Threfore, P (A)=33/100
P (A)=14/100.
Question 11.
The 5 numeric tiles
![]() are placed face down. You pick 4 tiles to form a 4-digit number. How many outcomes are favourable to the event of forming a number greater than 8,755?
are placed face down. You pick 4 tiles to form a 4-digit number. How many outcomes are favourable to the event of forming a number greater than 8,755?
Answer: 36
Explanation:
Let’s assume that the event is A.
Event A is the forming a 4-digit number greater than 8,755
we can pick 4 tiles such as 5, 6, 7, 8
Event A= 8756, 8757, 8758, 8765, 8766, 8767, 8768, 8775, 8776, 8777, 8778, 8785, 8786, 8787, 8788, 8885, 8886, 8887, 8888, and so on…