Math in Focus Grade 8 Chapter 1 Lesson 1.3 Answer Key The Power of a Power

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 1 Lesson 1.3 The Power of a Power to finish your assignments.

Math in Focus Grade 7 Course 3 A Chapter 1 Lesson 1.3 Answer Key The Power of a Power

Math in Focus Grade 8 Chapter 1 Lesson 1.3 Guided Practice Answer Key

Hands-On Activity

Materials:

• three stacks of five cards, each labeled with a number from

Explore The Power

In this activity, you and your partner will play a game in which you write and
evaluate expressions in the form (a^m)ⁿ.
You will get a point for each expression you write, and the person with the greater score wins.

Step 1.
Shuffle each stack of number cards and place them in a pile. Each player randomly draws three cards, one from each pile.

Step 2
Use your three cards to write an expression in the form (a^m)ⁿ.
For instance, if you draw 2, 4, and 5, you could write (2⁴)⁵,(4²)⁵, or another expression.
Write as many expressions as you can. You may want to use a calculator to evaluate your expression.
For instance, to evaluate (2⁴)⁵, you can use these keystrokes:

Step 3.
Record your expressions and their values.
Your partner should also record his or her expressions and their values.
Check your partner’s work.

Step 4.
Continue the game by replacing the cards you used and shuffling the piles.
Repeat Step 1 to Step 2 several more times. When you are finished,
find each player’s score by counting the number of correct expressions that
each player has written. The player with the greater score wins.

Math Journal Is it correct to assume that using the greatest number drawn as
the base will give the expression with the greatest possible value?
Explain or give an example.
Answer:
Yes,
Example: Drawing numbers 7,3,8,

Explanation:
Yes it is correct to assume that using the greatest number drawn as
the base will give the expression with the greatest possible value example
if we draw 7,3,8 we could write (8⁷)³,(7⁸)³.

Simplify each expression. Write your answer in exponential notation.

Question 1.
(5³)⁴
(5³)⁴ = Use the of a power property.
= Simplify.
Answer:
(5)¹²,

Explanation:
Given (5³)⁴ used the power of a power property and simplified as
(5)^3X4 = (5)¹².

Question 2.
(2.3⁴)²
(2.3⁴)² = Use the of a power property.
= Simplify.
Answer:
(2.3)⁸,

Explanation:
Given (2.3⁴)² used the power of a power property and simplified as
(2.3)^{4 X 2} = (2.3)⁸.

Question 3.
[(3p)⁵]⁴
Answer:
(3p)²⁰,

Explanation:
Given [(3p)⁵]⁴ used the power of a power property and simplified as
(3p)^{5 X 4} = (3p)²⁰.

Question 4.
[(-y)⁴]⁷
Answer:
(-y)²⁸,

Explanation:
Given (-y⁴)⁷ used the power of a power property and simplified as
(-y)^4X7 = (-y)²⁸.

Simplify each expression. Write your answer in exponential notation.

Question 5.
[(-3) • (-3)⁶]²

Answer:
(-3)¹⁴,

Explanation:

Question 6.
[p⁴ • p²]⁵

Answer:
(p)³⁰,

Explanation:

Question 7.
(6³ • 6³]⁷ ÷ 6¹⁰

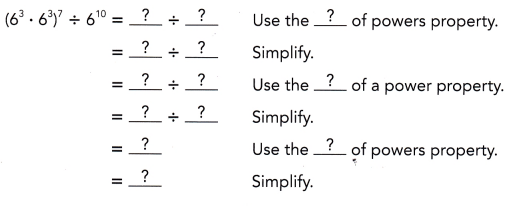
Answer:
(6)³²,

Explanation:

Question 8.

Answer:
(x)⁶,

Explanation:

Math in Focus Course 3A Practice 1.3 Answer Key

Simplify each expression. Write your answer in exponential notation.

Question 1.
(2⁶)²
Answer:
(2)¹²,

Explanation:
Given (2⁶)² used the power of a power property and simplified as
(2)^{6 X 2} = (2)¹².

Question 2.
(3⁴)³
Answer:
(3)¹²,

Explanation:
Given (3⁴)³ used the power of a power property and simplified as
(3)^{4 X 3} = (3)¹².

Question 3.
(10⁵)⁴
Answer:
(10)²⁰,

Explanation:
Given (10⁵)⁴ used the power of a power property and simplified as
(10)^{5 X 4} = (10)²⁰.

Question 4.
(10⁷)²
Answer:
(10)¹⁴,

Explanation:
Given (10⁷)² used the power of a power property and simplified as
(10)^{7X 2} = (10)¹⁴.

Question 5.
(25³)³
Answer:
(25)⁹,

Explanation:
Given (25³)³ used the power of a power property and simplified as
(25)^{3X 3} = (25)⁹.

Question 6.
(x⁶)³
Answer:
(x)¹⁸,

Explanation:
Given (x⁶)³ used the power of a power property and simplified as
(x)^{6 X 3} = (x)¹⁸.

Question 7.
\(\left[\left(\frac{1}{8}\right)^{3}\right]^{6}\)
Answer:
\([\left(\frac{1}{8}\right)^{18}\),

Explanation:
Given \([\left(\frac{1}{8}\right)^{3}]^{6}\)
used the power of a power property and simplified as
\([\left(\frac{1}{8}\right)^{3 X 6}\) =
\([\left(\frac{1}{8}\right)^{18}\).

Question 8.
\(\left[\left(\frac{4}{5}\right)^{2}\right]^{4}\)
Answer:
\([\left(\frac{4}{5}\right)^{8}\),

Explanation:
Given \(\left[\left(\frac{4}{5}\right)^{2}\right]^{4}\)
used the power of a power property and simplified as
\([\left(\frac{4}{5}\right)^{2X4}\) =
\([\left(\frac{4}{5}\right)^{8}\).

Question 9.
[(2y)³]⁸
Answer:
(2y)²⁴,

Explanation:
Given [(2y)³)]⁸ used the power of a power property and simplified as
(2y)^3X8 = (2y)²⁴.

Question 10.
[(57p)⁴]⁴
Answer:
(57p)¹⁶,

Explanation:
Given [(57p)⁴)⁴ used the power of a power property and simplified as
(57p)^{4 X 4} = (57)¹⁶.

Question 11.
[(-6)⁴]³
Answer:
(-6)¹²,

Explanation:
Given [(-6)⁴)³ used the power of a power property and simplified as
(-6)^4X3 = (-6)¹².

Question 12.
[(-p)²]¹¹
Answer:
(-p)²²,

Explanation:
Given [(-p)²]¹¹ used the power of a power property and simplified as
(-p)^2X11 = (-p)²².

Question 13.
Math Journal Michael thinks that (a³)² = a⁵. Is he correct? Why?

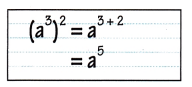
Answer:
No, Michael is not correct as [(a)³]² = (a)⁶≠(a)⁵,

Explanation:
Given (a³)² = a⁵ used the power of a power property and simplified as
(a)^3X2 = (a)⁶≠(a)⁵. Therefore Michael is incorrect.

Simplify each expression. Write your answer in exponential notation.

Question 14.
(5⁵ • 5⁶)²
Answer:
(5)²²,

Explanation:
Given ((5⁵ • 5⁶)² used the product of a power property as
(5⁵⁺⁶)² = (5¹¹)² and using power of power property simplified as
(5)^11X2 = (5)²².

Question 15.
(p⁴ • p²)⁶
Answer:
(p)⁴⁸,

Explanation:
Given ((5⁵ • 5⁶)² used the product of a power property as
(5⁵⁺⁶)² = (5¹¹)² and using power of power property simplified as
(5)^11X2 = (5)²².

Question 16.
\(\left[\left(\frac{1}{2}\right) \cdot\left(\frac{1}{2}\right)^{3}\right]^{5}\)
Answer:
\(\left[(\frac{1}{2}\right)^{20}\),

Explanation:
Given \(\left[\left(\frac{1}{2}\right) \cdot\left(\frac{1}{2}\right)^{3}\right]^{5}\)
Using the product of a power property as \(\left[\left(\frac{1}{2}\right)^{1+
3}\right]^{5}\) = \(\left[\left(\frac{1}{2}\right)^{4}\right]^{5}\) and using power of power property simplified as \(\left(\frac{1}{2}\right)^{4 X 5}\) = \(\left(\frac{1}{2}\right)^{20}\).

Question 17.
\(\left[\left(-\frac{4}{9}\right)^{2} \cdot\left(-\frac{4}{9}\right)^{3}\right]^{2}\)
Answer:
\(\left[(-\frac{4}{9}\right)^{10}\),

Explanation:
Given \(\left[\left(-\frac{4}{9}\right)^{2} \cdot\left(-\frac{4}{9}\right)^{3}\right]^{2}\)
Using the product of a power property as \(\left[\left(-\frac{4}{9}\right)^{2+
3}\right]^{2}\) = \(\left[\left(-\frac{4}{9}\right)^{5}\right]^{2}\) and using power of power property simplified as \(\left(-\frac{4}{9}\right)^{5 X 2}\) = \(\left(-\frac{4}{9}\right)^{10}\).

Question 18.
(2² • 2⁴)³ ÷ 2⁸
Answer:
2¹⁰,

Explanation:
Given (2² • 2⁴)³ ÷ 2⁸ used the product of a power property as
(2²⁺⁴)³  ÷ 2⁸  = (2⁶)³ ÷ 2⁸ and using power of power property simplified as
(2)^6X3 ÷ 2⁸  = ( 2)¹⁸ ÷2⁸ using division of power property ( 2)^18-8 = (2)¹⁰.

Question 19.
(7 • 7²)⁵ ÷ 7³
Answer:
^{( 7)12,}

Explanation:
Given (7 • 7²)⁵ ÷ 7³ used the product of a power property as
(7¹⁺²)⁵  ÷ 7³  = (7³)⁵ ÷ 7³ and using power of power property simplified as
(7)^3X5 ÷ 7³  = ( 7)¹⁵ ÷7³ using division of power property ( 7)^15-3 = ( 7)¹².

Question 20.
(s⁶ • s²) ÷ s⁴
Answer:
(s)⁴,

Explanation:
Given (s⁶ • s²) ÷ s⁴ used the product of a power property as
(s⁶⁺²) ÷ s⁴  = (s⁸) ÷ s⁴  using division of power property ( s)^8-4 = ( s)⁴.

Question 21.
(t⁴ • t⁴) ÷ t⁴
Answer:
(t)⁴,

Explanation:
Given (t⁴ • t⁴) ÷ t⁴ used the product of a power property as
(t⁴⁺⁴) ÷ t⁴  = (t⁸) ÷ t⁴  using division of power property (t)^8-4 = ( t)⁴.

Question 22.
\(\frac{\left(8^{8} \cdot 8^{3}\right)^{2}}{\left(8^{5}\right)^{4}}\)
Answer:
8²,

Explanation:
Given \(\frac{\left(8^{8} \cdot 8^{3}\right)^{2}}{\left(8^{5}\right)^{4}}\)  used the product of a power property as \(\frac{\left(8^{8+3}\right)^{2}}{\left(8^{5}\right)^{4}}\)
and using power of power property simplified as \(\frac{(8)^{11 X 2}}{(8)^{5 X 4}}\)
 using division of power property (8)^22-20 = (8)².

Question 23.
\(\frac{\left(3^{4} \cdot 3^{2}\right)^{4}}{\left(3^{5}\right)^{2}}\)
Answer:
3¹⁴,

Explanation:
Given \(\frac{\left(3^{4} \cdot 3^{2}\right)^{4}}{\left(3^{5}\right)^{2}}\) used the product of a power property as \(\frac{\left(3^{4+2}\right)^{4}}{\left(3^{5}\right)^{2}}\)
and using power of power property simplified as \(\frac{(3)^{6 X 4}}{(3)^{5 X 2}}\)
 using division of power property (3)^24-10 = (3)¹⁴.

Question 24.
\(\frac{\left(b \cdot b^{3}\right)^{5}}{\left(b^{2}\right)^{4}}\)
Answer:
b¹²,

Explanation:
Given \(\frac{\left(b \cdot b^{3}\right)^{5}}{\left(b^{2}\right)^{4}}\) used the product of a power property as \(\frac{\left(b^{1+3}\right)^{5}}{\left(b^{2}\right)^{4}}\)
and using power of power property simplified as \(\frac{(b)^{4 X 5}}{(b)^{2X 4}}\)
 using division of power property (b)^20-8 = (b)¹².

Question 25.
\(\frac{\left(h^{6} \cdot h^{6}\right)^{2}}{\left(h^{3}\right)^{5}}\)
Answer:
h⁹,

Explanation:
Given \(\frac{\left(h^{6} \cdot h^{6}\right)^{2}}{\left(h^{3}\right)^{5}}\) used the product of a power property as \(\frac{\left(h^{6+6}\right)^{2}}{\left(h^{3}\right)^{5}}\)
and using power of power property simplified as \(\frac{(h)^{12 X 2}}{(h)^{3X 5}}\)
 using division of power property (h)^24-15 = (h)⁹.

Question 26.
(q⁵ • q²)³) ÷ 5q⁵
Answer:
(q)¹⁶÷ 5 or 1/5 . q¹⁶,

Explanation:
Given ((q⁵ • q²)³) ÷ 5q⁵  used the product of a power property as
((q⁵⁺²)³) ÷ 5q⁵  and using power of power property simplified as ((q)^{7 X 3} ) ÷ 5q⁵  using
division of power property (q)^21-5 ÷ 5 = (q)¹⁶÷ 5 or 1/5 . q¹⁶.

Question 27.
(c⁷ • q³)⁴ ÷ 6c²
Answer:
(c²⁶• q¹²) ÷ 6 or 1/6 . q¹⁶,

Explanation:
Given ((c⁷ • q³)⁴) ÷ 6c² using power of power property simplified as
((c)^{7 X4} • q^3X4) ÷ 6c²  using division of power property ((c)^28-2 • q¹² ) ÷ 6 =
(c²⁶• q¹²) ÷ 6 or 1/6 . q¹⁶.

Question 28.

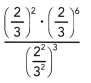
Answer:
\(\left(\frac{2}{3}\right)^{2}\),

Explanation:
Given (\(\left[(\frac{2}{3}\right)^{2}\) . \(\left[(\frac{2}{3}\right)^{6}\))÷\(\left[(\frac{2}{3}\right)^{2 X 3}\)] using product of power property simplified as
\(\left(\frac{2}{3}\right)^{2+ 6}\) ÷\(\left(\frac{2}{3}\right)^{6}\) using
division of power property \(\left[(\frac{2}{3}\right)^{8-6}\)] we get
\(\left(\frac{2}{3}\right)^{2}\).

Question 29.

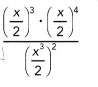
Answer:
\(\left(\frac{x}{2}\right)^{1}\),

Explanation:
Given (\(\left[(\frac{x}{2}\right)^{3}\) . \(\left[(\frac{x}{2}\right)^{4}\))÷\(\left[(\frac{x}{2}\right)^{3 X 2}\)] using product of power property simplified as
\(\left(\frac{x}{2}\right)^{3+ 4}\) ÷\(\left(\frac{x}{2}\right)^{6}\) using
division of power property \(\left[(\frac{x}{2}\right)^{7-6}\)] we get
\(\left(\frac{x}{2}\right)^{1}\).