This handy Math in Focus Grade 5 Workbook Answer Key Chapter 13 Practice 3 Right, Isosceles, and Equilateral Triangles provides detailed solutions for the textbook questions.
Math in Focus Grade 5 Chapter 13 Practice 3 Answer Key Right, Isosceles, and Equilateral Triangles
Complete. ABC and EFG are right triangles.
Question 1.
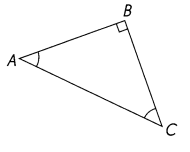
m∠B =___
m∠A + m∠C = ___
= ____
Answer:
m∠B =90°
m∠A + m∠C = 90°
Explanation:
Properties of Right – Angled Triangle
- One angle of the triangle always measures 90degree.
- The hypotenuse is the longest side of the right-angle triangle.
- The side that is opposite to the 90degree angle is the hypotenuse.
- The Sum of two interior angles of the right-angled triangle is always 90degree.
Question 2.
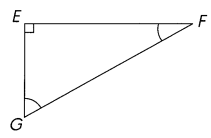
m∠E = ___
m∠F + m∠G = ___
Answer:
m∠E = 90°
m∠F + m∠G = 90°
Explanation:
Properties of Right – Angled Triangle
- One angle of the triangle always measures 90°.
- The hypotenuse is the longest side of the right-angle triangle.
- The side that is opposite to the 90° angle is the hypotenuse.
- The Sum of two interior angles of the right-angled triangle is always 90degree.
Measure the angles of the triangle. Then fill in the blanks.
Question 3.
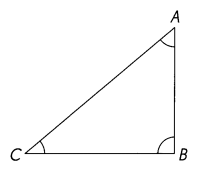
m∠A _____
m∠B ______
m∠C ______
m∠A + m∠C ______
Answer:
m∠B = 90°
m∠C = 40°
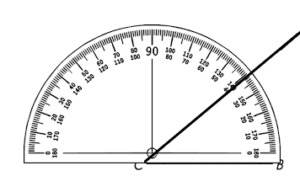
m∠A = 50°
Explanation:
Sum of angles in a triangle are 180°
40 + 90 = 130
180 – 130 = 50
m∠A = 50°
m∠A + m∠C = 50° + 40° = 90°
These triangles are not drawn to scale. Identify and shade the right triangles.
Question 4.
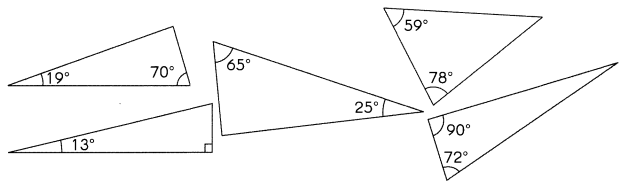
Answer:
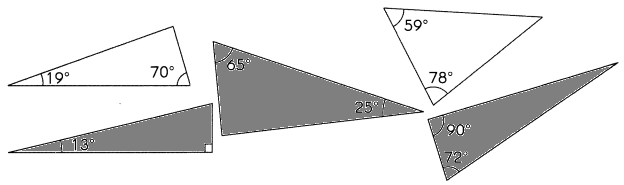
Explanation:
- One angle of the triangle always measures 90°.
- The hypotenuse is the longest side of the right-angle triangle.
- The side that is opposite to the 90° angle is the hypotenuse.
- The Sum of two interior angles of the right-angled triangle is always 90degree.
These triangles are not drawn to scale. Find the unknown angle measures.
Question 5.
Find the sum of the measures of ∠A and ∠B.
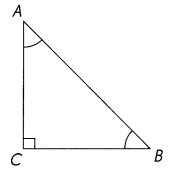
Answer:
∠A + ∠B = 90°
Explanation:
Properties of Right – Angled Triangle
- One angle of the triangle always measures 90°.
- The hypotenuse is the longest side of the right-angle triangle.
- The side that is opposite to the 90° angle is the hypotenuse.
- The Sum of two interior angles of the right-angled triangle is always 90degree.
Question 6.
Find the measure of ∠C.
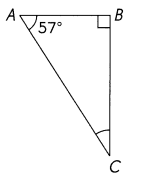
Answer:
33°
Explanation:
Properties of Right – Angled Triangle
- The Sum of two interior angles of the right-angled triangle is always 90degree.
So in right angle triangle, Sum of other two angles is 90°.
So ∠C = 90 – 57 = 33
Question 7.
Find the measure of ∠ADC and ∠ABC.
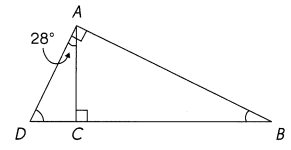
Answer:
∠ADC =62°
∠ABC =28°
Explanation:
In Triangle DAB, ∠DAB =90°
In Triangle ABC, ∠ACB=90°
In Triangle ACD, ∠ACD=90°
and ∠DAC=28°
So ∠ADC = 180° -(∠ACD +∠DAC) = 180° -(90°+28°) = 180° -(118°) =62°
∠BAC = ∠DAB – ∠DAC = 90° -28° = 62°
∠ABC =180° -(∠ACB +∠BAC) = 180° -(90°+62°) = 180° -(152°) =28°
Question 8.
Find the measures of ∠EGF and ∠DGE.
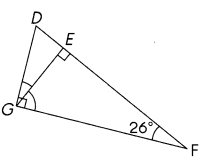
Answer:
∠EGF =64°
∠DGE = 26°
Explanation:
In Triangle DGF, ∠DGF=90°
In Triangle GEF, ∠GEF=90° and ∠EFG=26°
In Triangle DEG, ∠DEG=90°
So ∠EGF= 180° -(∠GEF+∠EFG) = 180° -(90°+26°) = 180° -(116°) =64°
∠DGE= ∠DGF- ∠EGF= 90° -64° = 26°
Complete. XYZ and PQR are isosceles triangles.
Question 9.
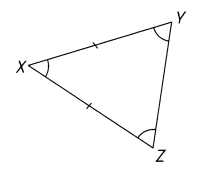
Which two sides are of equal length?
________
Which two angles have equal measures?
_________
Answer:
XY and XZ sides are equal length.
∠Z and ∠Y angles have equal measures.
Explanation:
- It has two sides of equal length.
- The angles opposite to equal sides are equal in measure
Question 10.
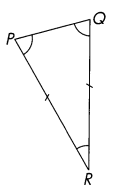
Which two sides are of equal length?
_________
Which two angles have equal measures?
________
Answer:
PR and QR sides are of equal length.
∠P and ∠Q angles have equal measures.
Explanation:
An Isosceles Triangle has the Following Properties:
- It has two sides of equal length.
- The angles opposite to equal sides are equal in measure
These triangles are not drawn to scale. Find the unknown angle measures.
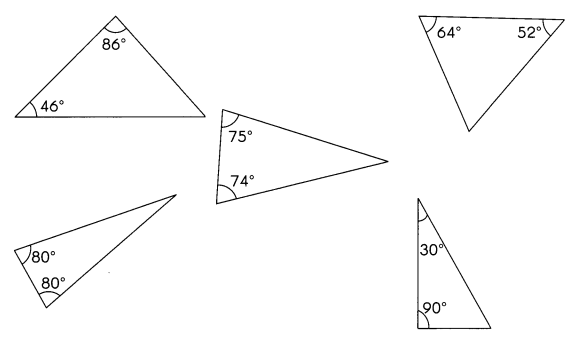
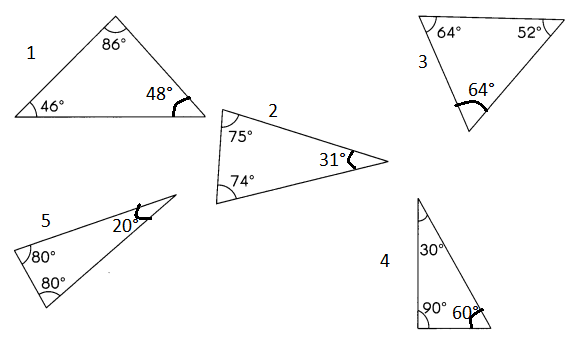
Question 11.
Answer:
Explanation:
The properties of a triangle are:
- The sum of all internal angles of a triangle is always equal to 180°. This is called the angle sum property of a triangle. So,
1. 180 – (46 + 86) = 48
2. 180 – (75+74) = 31
3. 180 – (64 +52) = 64
4. 180 – (90 + 30 ) = 60
5. 180 – (80 + 80 ) = 20
These triangles are not drawn to scale. Find the unknown angle measures.
Question 12.
Find the measure of ∠F.
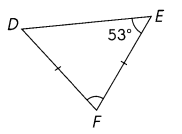
Answer:
∠F = 74°
Explanation:
The property of a triangle is : The sum of all internal angles of a triangle is always equal to 180°.
∠D + ∠F = 180 – 53 = 127 °
So ∠D = ∠E Then ∠D = 53 °
then ∠F = 127 – 53 =74°
Question 13.
Find the measure of ∠C.
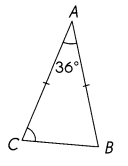
Answer:
∠C =72°
Explanation:
The property of a triangle is: The sum of all internal angles of a triangle is always equal to 180°.
∠C + ∠B = 180 – 36 = 144°
An Isosceles Triangle has the Following Property: The angles opposite to equal sides are equal in measure
So ∠C = ∠B Then 144/2 =72°
then ∠C =72°
Question 14.
Find the measure of ∠TRS.
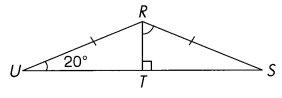
Answer:
∠TRS = 180 – (∠RST+∠RTS)=180 – (20+90) = 70°
Explanation:
Triangle URS is a Isosceles Triangle.
An Isosceles Triangle has the Following Property: The angles opposite to equal sides are equal in measure Then
∠U= ∠S = 20°
The property of a triangle is : The sum of all internal angles of a triangle is always equal to 180°.
In Triangle TRS ,
∠RST = 20°
∠RTS = 90°
∠TRS = 180 – (∠RST+∠RTS)=180 – (20+90) = 70°
Question 15.
Find the measure of ∠d.
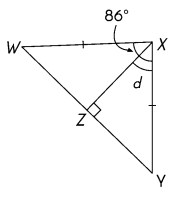
Answer:
∠d = 172°
Explanation:
Triangle WXY is a Isosceles Triangle.
An Isosceles Triangle has the Following Property: The angles opposite to equal sides are equal in measure Then
then ∠W= ∠Y
Triangle WXZ a Right angle Triangle.
then ∠WZX = 90°
∠WXZ=86°
The property of a triangle is : The sum of all internal angles of a triangle is always equal to 180°.
In Triangle WZX,
∠XWZ = 180 – (∠WZX+∠WXZ )=180 – (90+86) = 4°
In Triangle WXY , ∠W= ∠Y = 4°
∠d = 180 – (4+4) = 172°
Complete. Use your protractor and centimeter ruler to measure the sides and angles. Which figure is an equilateral triangle? Check the box.
Question 16.
AB = __ cm
BC = __ cm
AC = ___ cm
m∠A = ___
m∠B = ___
m∠C = ____ ![]()
Answer:
Question 17.
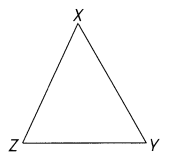
XY = __ cm
YZ = __ cm
XZ = ___ cm
m∠X = ___
m∠Y = ___
m∠Z = ____ ![]()
Answer:

Explanation:
XY = 4 cm
YZ = 4 cm
XZ = 4 cm
m∠X = 60°
m∠Y = 60°
m∠Z = 60°
Explanation:
The angles and sides are equal
Complete. ABC is an equilateral triangle.
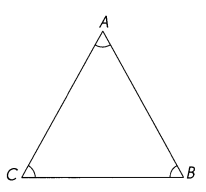
Question 18.
Which angles have measures equal to the measure of ∠A?
Answer:
∠A = ∠B = ∠C
Explanation:
- Three sides are equal.
- Three angles are equal i.e 60° each.
Question 19.
Which sides have lengths equal to the length of \(\overline{A B}\)?
Answer:
\(\overline{A B}\)= \(\overline{B C}\) = \(\overline{A C}\)
Explanation:
- Three sides are equal.
- Three angles are equal i.e 60° each.
Question 20.
What can you say about the angles of triangle ABC ?
Answer:
All angles are equal and 60° each.
Explanation:
- Three sides are equal.
- Three angles are equal i.e 60° each.
These triangles are not drawn to scale. Identify and shade the equilateral triangles.
Question 21.
Answer:
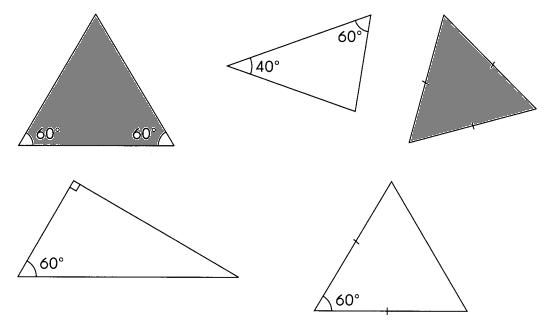
Explanation:
Properties of an Equilateral Triangle
- Three sides are equal.
- Three angles are equal i.e 60° each.
These triangles are not drawn to scale. Find the unknown angle measures.
Question 22.
Find the measure of ∠Q.
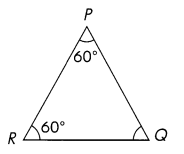
Answer:
∠Q = 60°
Explanation:
The property of a triangle is : The sum of all internal angles of a triangle is always equal to 180°.
∠Q = 180 – ∠P + ∠R = 180 – 60 + 60 = 60°
Question 23.
Find the measures of ∠Y and ∠Z
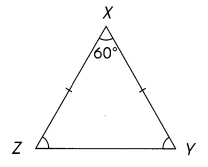
Answer:
∠Y =∠Z= 60°
Explanation:
The property of a triangle is : The sum of all internal angles of a triangle is always equal to 180°.
∠Z + ∠Y = 180 – ∠X = 180 – 60 = 120°
As per diagram Triangle XYZ is a Isosceles Triangle.
An Isosceles Triangle has the Following Property: The angles opposite to equal sides are equal in measure Then
∠Y =∠Z
then ∠Y =∠Z= 120°/2 = 60°
These triangles are not drawn to scale. Find the unknown angle measures.
Question 24.
WX = XY = YW. Find the measure of ∠d.
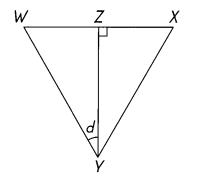
Answer:
Explanation:
WX = XY = YW So Triangle WXY is a Equilateral Triangle So Three angles are equal
∠WXY = 60°
∠XWY= 60°
∠WYX= 60°
So In Triangle XYZ,
∠ZXY= 60°
∠XZY= 90°
∠XYZ= 180 – 90 + 60=30°
∠d = ∠WYX -∠XYZ =60 – 30 =30°
Question 25.
Find the measure of ∠e.
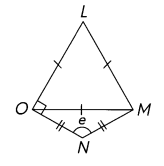
Answer:
∠e = 120°
Explanation:
∠LON = 90° given
As the triangle is equalateral the angles are equal
so the measure of ∠LOE = 60°
∠LMO = 60°
NOM triangle is an isosceles triangle
90 – 60 = 30°
∠MON = 30°
∠OMN = 30°
30° + 30° = 60°
180° – 60° = 120°
∠e = 120°
Question 26.
Triangle PQR is an equilateral triangle. Triangle PST is an isosceles triangle. The measures of ∠a, ∠b, and ∠c are the same. Find the measure of ∠d.
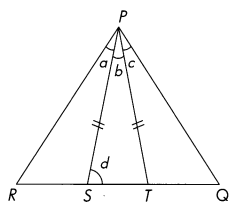
Answer:
∠d. = 80°
Explanation:
Triangle PQR is an equilateral triangle.
In equilateral triangle all angles are equal
sum of angles in a triangle are 180°
Triangle PST is an isosceles triangle.
The measures of ∠a, ∠b, and ∠c are the same.
so, ∠a, ∠b, and ∠c = 60°
20° + 20° + 20° = 60°
In isosceles triangle
The isosceles triangle property states that when two sides are equal, the base angles are also equal
so, 180° – 20° = 160°
80° + 80 °= 160°
∠d. = 80°