Practice the problems of Math in Focus Grade 5 Workbook Answer Key Cumulative Review Chapters 8 to 10 to score better marks in the exam.
Math in Focus Grade 5 Cumulative Review Chapters 8 to 10 Answer Key
Concepts and Skills
Mark ✗ to show where each decimal is located on the number line. (Lesson 8.1)
Question 1.
0.032

Answer:

Explanation:
In math, a number line can be defined as a straight line with numbers placed at equal intervals or segments along its length.
To represent a decimal on a number line, divide each segment of the number line into ten equal parts.
Then mark the given number on number line.
Question 2.
0.047
Answer:

Explanation:
In math, a number line can be defined as a straight line with numbers placed at equal intervals or segments along its length.
To represent a decimal on a number line, divide each segment of the number line into ten equal parts.
Then mark the given number on number line.
Complete. (Lesson 8.1)
Question 3.
3 tenths 5 hundredths = _________ thousandths
Answer:
0.350
3 tenths 5 hundredths = 0.305________ thousandths
Explanation:
Read the whole set of three decimal digits as a number, and say, “tenths”, “hundredths” and “thousandths.” 0.305 has 3 tenths, 0 hundredths, and 5 thousandths. While 0.305 is the sum of 3/10, 0/100, and 5/1000, it is also 305/1000
Just as “ones,” “tens,” and “hundreds” are used to describe place value for whole numbers,
there are terms that describe place value for decimals:
tenths, hundredths, thousandths, ten thousandths, hundred thousandths, millionths, etc.
These terms are used from left to right, starting with the first numeral after the decimal point.
Question 4.
803 thousandths = ______ tenths _______ thousandths
Answer:
803 thousandths = 8 tenths 0 hundredths 3 thousandths
Explanation:
Just as “ones,” “tens,” and “hundreds” are used to describe place value for whole numbers,
there are terms that describe place value for decimals:
tenths, hundredths, thousandths, ten thousandths, hundred thousandths, millionths, etc.
These terms are used from left to right, starting with the first numeral after the decimal point.
Question 5.
0.835 = 8 tenths 3 hundredths _____ thousandths
Answer:
0.835 = 8 tenths 3 hundredths 5 thousandths
Explanation:
Just as “ones,” “tens,” and “hundreds” are used to describe place value for whole numbers,
there are terms that describe place value for decimals:
tenths, hundredths, thousandths, ten thousandths, hundred thousandths, millionths, etc.
These terms are used from left to right, starting with the first numeral after the decimal point.
Write the equivalent decimal. (Lesson 8.1)
Question 6.
8 ones and 214 thousandths = __________
Answer: 8.214
Explanation:
The first digit to the right of decimal point is in the tenths place.
The second digit to the right of decimal point is in the hundredths place.
The third digit to the right of decimal point is in the thousandths place.
So, 8 ones and 214 thousandths.
Question 7.
1,180 thousandths = __________
Answer: 1.180
Explanation:
If you divide 1180 by one thousand you get 1180 thousandths as a decimal which is 1.180.
1180 thousands = 1180/1000 = 1.180
Question 8.
7\(\frac{60}{1000}\) = __________
Answer: 7.06
Explanation:
7 x 1000 + 60 = 7000 + 60 = 7060
\(\frac{7060}{1000}\) = 7.06
7\(\frac{60}{1000}\) = 7.06
Question 9.
\(\frac{6050}{1000}\) = __________
Answer: 6.05
Explanation:
The easiest way to convert a fraction to a decimal is to divide the numerator by the denominator.
Or else count the number of zeros in denominator and place the decimal in the given number by moving from right.
\(\frac{6050}{1000}\) = 6.05
4.526 can be written in expanded form as 4 + 0.5 + 0.02 + 0.006. Write each decimal in expanded notation. (Lesson 8.1)
Question 10.
0.329 = ___ + ___ + ___
Answer:
0.329 = 0.3 + 0.02 + 0.009
Explanation:
Writing decimals in expanded form simply means writing each number according to its place value.
This is done by multiplying each digit by its place value and adding them together.
20.125 = ___ + ___ + ___ + ___
Answer:
20.125 =20 + 0 + 0.1 + .02 + 0.005
Explanation:
Writing decimals in expanded form simply means writing each number according to its place value.
This is done by multiplying each digit by its place value and adding them together.
Complete. (Lesson 8.1)
In 9.168,
Question 12.
the digit 6 is in the ___ place.
Answer:
Hundredths place
Explanation:
Writing decimals in expanded form simply means writing each number according to its place value.
This is done by multiplying each digit by its place value and adding them together.
The digit 6 is in the hundredths place in 9.168.
Question 13.
the value of the digit 8 is ___
Answer:
Thousands place
Explanation:
Writing decimals in expanded form simply means writing each number according to its place value.
This is done by multiplying each digit by its place value and adding them together.
The digit 8 is in the thousandths place in 9.168.
Question 14.
the digit 1 stands for _______
Answer:
Tenths place
Explanation:
Writing decimals in expanded form simply means writing each number according to its place value.
This is done by multiplying each digit by its place value and adding them together.
The digit 1 is in the tenths place in 9.168.
Compare. Write >, <, or =. (Lesson 8.2)
Question 15.
1.07 ![]() 1.7
1.7
Answer: <
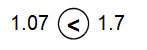
Explanation:
The value 1.07 is less than the other value 1.7, we use less than.
The symbol used to represent less than is “<”.
As there is no value for zero after decimal.
Question 16.
3.562 ![]() 3.526
3.526
Answer: >
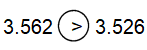
Explanation:
The value 3.562 is greater than the other value 3.526,
The symbol used to represent greater than is “>”.
The number after decimal is more in 562 than in 526.
Question 17.
15.4 ![]() 15.40
15.40
Answer: =
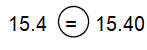
Explanation:
The value 15.4 is equal to 15.40,
In decimal if zero is present in ones place there is no value.
Order the decimals. (Lesson 8.2)
Question 18.
2.08, 1.973, 6.1
Begin with the least:
_____________
Answer:
1.973 , 2.08, 6.1
Explanation:
Arranging the numbers from least to greatest is known as Ascending order.
Question 19.
1.567, 1.667, 1.376
Begin with the greatest:
________________
Answer:
1.667, 1.567, 1.376
Explanation:
Arranging the numbers from least to greatest is known as Descending order.
Fill in the blanks. (Lesson 8.2)
Question 20.
The mass of a strand of hair is 0.179 gram.
Round the mass to the nearest hundredth of a gram.
0.179 gram rounds to ___ gram.
Answer: 0.18
0.179 gram rounds to 0.18 gram.
Explanation:
For rounding decimal numbers to the nearest hundredth,
we need to know the decimal place values of the digits in the given number.
This refers to the digits given before the decimal point as well as the digits given after the decimal point.
It should be noted that when we round numbers to the nearest hundredth,
we always use the thousandths place to decide whether the hundredths place will round up or will remain the same.
Question 21.
The length of a rope is 2.589 yards.
Round the length to the nearest tenth of a yard.
2.589 yards rounds to ___ yards.
Answer: 2.6
2.589 yards rounds to 2.6 yards
Explanation:
For rounding decimal numbers to the nearest hundredth,
we need to know the decimal place values of the digits in the given number.
This refers to the digits given before the decimal point as well as the digits given after the decimal point.
It should be noted that when we round numbers to the nearest hundredth,
we always use the thousandths place to decide whether the hundredths place will round up or will remain the same.
Write each decimal as a mixed number in simplest form. (Lesson 8.3)
Question 22.
6.2 = ___
Answer:
6\(\frac{1}{5}\)
Explanation:
\(\frac{62}{10}\)
6\(\frac{2}{10}\)
6\(\frac{1}{5}\)
Question 23.
2.16 = _______
Answer:
2\(\frac{4}{25}\)
Explanation:
\(\frac{216}{100}\)
2\(\frac{16}{100}\)
2\(\frac{4}{25}\)
Multiply. (Lessons 9.7 and 9.2)
Question 24.
29.3 × 8 = _______
Answer: 234.4
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.
Question 25.
12.08 × 5 = _______
Answer: 60.4
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.
Question 26.
86.4 × 10 = _______
Answer: 864
Explanation:
Separate 10 as 1 ones and 0 tenths,
then multiply with ones first and later tens.
86.4 x 10 = (86.4 x 1) x 10
= 86.4 x 10
= 864
So, 86.4 x 10= 864
Question 27.
13.5 × 30 = ____
Answer: 405
Explanation:
Separate 30 as 3 ones and 1 tenths,
then multiply with ones first and later tens.
13.5 x 30 = (13.5 x 3) x 10
= 40.5 x 10
= 405
So, 13.5 x 30= 405
Question 28.
73.96 × 100 = ___
Answer:7,396
Explanation:
73.96 x 100 = (73.96 x10) x 10
=739.6 x 10
=7396
So, 73.96 x 100 = 7,396
Question 29.
6.2 × 700 = ___
Answer: 4,340
Explanation:
6.2 x 700 = (6.2 x70) x 10
= 434 x 10
=4340
So, 6.2 x 700 = 4,340
Question 30.
9.34 × 1,000 = ___
Answer: 9,340
Explanation:
9.34 x 1000 = (9.34 x 10) x 10 x 10
= 93.4 x 10 x 10
=934 x 10
= 9340
So, 9.34 x 1000 = 9,340
Question 31.
25.6 × 9,000 = ____
Answer: 230,400
Explanation:
25.6 x 1000 = (25.6 x 9) x 10 x 10
= 230.4 x 10 x 10
=2304 x 100
= 230400
So, 25.6 x 1000 = 230,400
Divide. (Lesson 9.3)
Question 32.
0.5 ÷ 5 = _______
Answer: 0.1
Explanation:
0.5 ÷ 5 = 5 tenths ÷ 5
= 1 tenths
= 0.1
So, 0.5 ÷ 5 = 0.1
Question 33.
0.63 ÷ 9 = ___
Answer: 0.07
Explanation:
0.63 ÷ 9 = 63 hundredths ÷ 9
=7 hundredths
= 0.07
So, 0.63 ÷ 9 = 0.07
Question 34.
36.8 ÷ 4 = ___
Answer: 9.2
Explanation:
Step 1
Divide the ones by 4.
36 ones ÷ 4 = 9 ones R 0 ones
Regroup the remainder into tenths.
0 ones = 0 tenths
Add the tenths.
0 tenths + 8 tenths = 8 tenths
Step 2
Divide the tenths by 4.
8 tenths ÷ 4 = 2 tenths
So, 36.8 ÷ 4 = 9.2
Question 35.
96.3 ÷ 5 = ___
Answer: 19.26
Explanation:
Step 1
Divide the ones by 5.
96 ones ÷ 5 = 19 ones R 2 ones
Regroup the remainder into tenths.
192 = 19 ones and 2 tenths
Step 2
Divide the tenths by 5.
10 tenths ÷ 5 = 2 tenths
So, 96.3 ÷ 5 = 19.26
Question 36.
3.36 ÷ 4 = ___
Answer: 0.84
Explanation:
Step 1
Divide the ones by 4.
3 ones ÷ 4 = 8 ones R 7 ones
Regroup the remainder into tenths.
0 ones = 0 tenths
Add the tenths.
0 tenths + 8 tenths = 8 tenths
Step 2
Divide the tenths by 4.
8 tenths ÷ 4 = 2 tenths
So, 3.36 ÷ 4 = 0.84
Question 37.
1.92 ÷ 8 = ___
Answer: 24
Explanation:
Step 1
Divide the ones by 8.
9 ones ÷ 8 = 1 ones R 1 ones
Regroup the remainder into tenths.
1 ones = 10 tenths
Add the tenths.
10 tenths + 9 tenths = 19 tenths
Step 2
Divide the tenths by 4.
19 tenths ÷ 8 = 4 tenths
So, 1.92 ÷ 8 = 24
Divide. Round the quotient to the nearest tenth and nearest hundredth. (Lesson 9.3)
Question 38.
19 ÷ 7 = ___ to the nearest tenth
19 ÷ 7 = ___ to the nearest hundredth
Answer:
19 ÷ 7 = 2.7 to the nearest tenth
19 ÷ 7 = 0.27 to the nearest hundredth
Explanation:
19 ÷ 7 = 2.7 to the nearest tenth
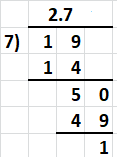
19 ÷ 7 = 0.27 to the nearest hundredth
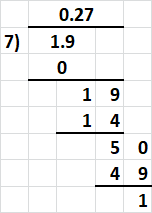
19 ÷ 7 = 2.7_ to the nearest tenth
First, divide to two decimal places.
Then round the answer to the nearest tenth.
Explanation:
19 ÷ 7 = ___ to the nearest hundredth
First, divide to three decimal places.
Then round the answer to the nearest hundredth.

Divide. (Lesson 9.4)
Question 39.
3.8 ÷ 10 = ___
Answer: 0.38
Explanation:
3.8 ÷ 10 = (4.8 ÷ 1 ) ÷ 10
= 3.8 ÷ 10
= 0.38
So, 3.8 ÷ 10 = 0.38
Question 40.
19.6 ÷ 20 = ___
Answer: 0.98
Explanation:
When dividing by ten, move the decimal point one place to the left.
Place value is the value of a digit based on its location in the number,
19.6 ÷ 20 = (19.6 ÷ 2 ) ÷ 10
= 9.8 ÷ 10
= 0.98
So, 19.6 ÷ 10 = 0.98
Question 41.
4.5 ÷ 100 = ___
Answer: 0.045
Explanation:
4.5 ÷ 100 = (4.5 ÷ 10 ) ÷ 10
= 0.45 ÷ 10
= 0.045
So, 4.5 ÷ 100 = 0.045
Question 42.
375 ÷ 300 = ___
Answer: 1.25
Explanation:
375 ÷ 300 = (375 ÷ 30 ) ÷ 10
= 12.5 ÷ 10
= 1.25
So, 375 ÷ 300 = 1.25
Question 43.
5,030 ÷ 1,000 = ___
Answer: 5.03
Explanation:
5030 ÷ 1000 = (5030 ÷ 10 ) ÷ 10 ÷ 10
= 503 ÷ 10÷ 10
= 50.3÷ 10
=5.03
So, 5030 ÷ 1000 = 5.03
Question 44.
2,506 ÷ 7,000 = ___
Answer: 0.358
Explanation:
2506 ÷ 7000 = (2506 ÷ 70 ) ÷ 10 ÷ 10
= 35.8 ÷ 10÷ 10
= 3.58÷ 10
=0.358
So, 2506 ÷ 7000 = 0.358
Estimate each answer by rounding the numbers to an appropriate place. (Lesson 9.5)
Question 45.
91.2 + 25.9
Answer: 117.1
Estimate: 117
Explanation:
91.2 + 25.9
91.2 rounds to 91.
25.9 rounds to 26.
91 + 26 = 10
91.2 + 25.9 is about 117.
Question 46.
37.4 – 11.7
Answer: 25.7
Estimate: 25
Explanation:
37.4 – 11.7
37.4 rounds to 37.
11.7 rounds to 12.
37 – 12 = 25
37.4 – 11.7 is about 25.
Question 47.
21.63 × 5
Answer: 108.15
Estimate: 110
Explanation:
21.63 × 5
21.63 rounds to 22.
22 × 5 = 110
21.63 × 5 is about 110.
Question 48.
7.05 ÷ 8
Answer: 0.88
Estimate: 1
Explanation:
7.05 ÷ 8
7.05 is about 8.
8 ÷ 8 = 1
7.05 ÷ 8 is about 1.
Write each ratio in three ways. Complete the table. (Lesson 10.1)
Question 49.

Answer:

Explanation:
Ratios are smaller to fractions, and each fraction can be written as a fraction.
Divide the first number 23 by the second number 100.
Multiply by 100 to convert to a percentage.
Add the percent symbol (%) to the output.
To change a percent to a decimal we divide by 100.
This is the same as moving the decimal point two places to the left.
Question 50.

Answer:

Explanation:
Ratios are smaller to fractions, and each fraction can be written as a fraction.
Divide the first number 23 by the second number 100.
Multiply by 100 to convert to a percentage.
Add the percent symbol (%) to the output.
To change a percent to a decimal we divide by 100.
This is the same as moving the decimal point two places to the left.
Express each fraction as a percent. (Lesson 10.2)
Question 51.
\(\frac{88}{200}\) =
Answer: 44%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .
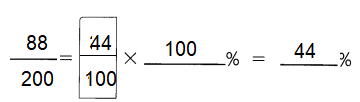
Question 52.
\(\frac{204}{400}\) =
Answer: 51%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .
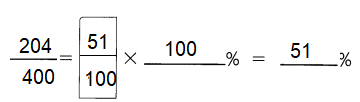
Question 53.
\(\frac{6}{20}\) =
Answer: 30%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .
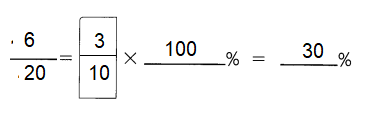
Question 54.
\(\frac{7}{50}\) =
Answer: 14%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .
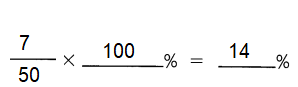
Question 55.
\(\frac{13}{20}\) =
Answer: 65%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .
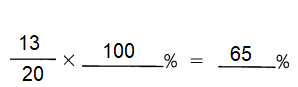
Question 56.
\(\frac{16}{25}\) =
Answer: 64%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .
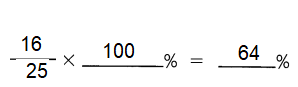
Problem Solving
Solve.
Question 57.
Hazel saves $5.75 each week.
a. How much does she save in 2 weeks?
Answer: $11.5
Estimate: 12
Explanation:
Hazel saves $5.75 each week.
Total amount she saves in two weeks
5.75 x 2 = 11.5
5.75 is rounded as 6
6 x 2 = 12
So, 5.75 x 2 is about 12.
b. She spends $23.83 on a book and $9.12 on a wallet. How much does she spend on the two items?
Answer: $32.95
Estimate: 33
Explanation:
Hazel spends $23.83 on a book and $9.12 on a wallet.
Total amount she spend on the two items
23.83 + 9.12
23.83 rounds as 24
9.12 rounds as 9
So, 24 + 9 = 33
23.83 + 9.12 = 32.95
Question 58.
Evelyn has 12.7 quarts of fruit punch in a cooler. She pours the fruit punch into glasses. She fills 5 glasses, each with a capacity of 0.36 quart. Then she fills 8 glasses, each with a capacity of 0.52 quart. How much fruit punch is left in the cooler?
Answer:
Explanation:
total fruit punch = 12.7 quarts
she fills 5 glasses with 0.36 quart
she fills 8 glasses with 0.52 quart
totalt fruit punch that she filled in glasses = 5 x 0.36 + 8 x 0.52
= 1.8 + 4.16 = 5.96 quarts
total fruit punch left in cooler = 12.7 – 5.96 = 6.74 quarts
Solve. Use models to help you.
Question 59.
The total weight of three tables is 16.9 pounds. The first table is twice as heavy as the second table. The weight of the third table is \(\frac{1}{3}\) the weight of the second table. What is the weight of the first table?
Answer:
weight of first table = 10.14 pounds
Explanation:
let weight of second table is x
weight of first table = 2 x weight of second table
weight of first table = 2x
weight of third table = \(\frac{1}{3}\) of weight of third table
weight of third table = \(\frac{1}{3}\) x
So we get,
weight of first table = 2x
weight of second table = x
weight of third table = \(\frac{1}{3}\) x
total weight = 16.9 pounds
first table + second table + third table = 16.9 pounds
2x + x + \(\frac{1}{3}\) x = 16.9
3x + \(\frac{1}{3}\) x = 16.9
\(\frac{3 x (3x) + x}{3}\) = 16.9
9x + x = 16.9 x 3
10x = 50.7
x = \(\frac{50.7}{10}\)
x = 5.07
weight of first table = 2x = 2 x 5.07
weight of first table = 10.14 pounds
Question 60.
There are 950 seats in a theater. 82% of the seats are occupied. How many seats are not occupied?
Answer:
151 seats
Explanation:
Total number of seats = 950
Occupied seats = 950 x \(\frac{82}{100}\) = 799
Seats not occupied = 950 – 799 = 151 seats
Solve. Use models to help you.
Question 61.
Rahul spends 10% of his weekly allowance on Monday. On Wednesday, he spends \(\frac{1}{3}\) of the remainder. What percent of his allowance is left at the end of Wednesday?
Answer: 60%
Explanation:
x 100% – x10% =x 90%
x 90% x \(\frac{1}{3}\)
x 30% he spent on Wednesday
total he spent 10% + 30% = 40%
percent of his allowance is left at the end of Wednesday is 60%
Question 62.
Ms. Jones buys a violin for $860. In addition, she has to pay 7% sales tax. How much does she pay in all?
Answer: $920.2
Estimate: $920
Explanation:
860 x \(\frac{7}{100}\) = 60.2 tax
she pay in all $860 + $60.2 = $920.2
Solve.
Question 63.
The regular price of a television set is $1,200. Albert buys the television set at a discount of 35%. How much does he pay for the television set?
Answer: $780
Explanation:
1200 x \(\frac{35}{100}\) = 420
1200 – 420 = 780
Albert pay for the television set $780
Question 64.
A school band gives a year-end concert. It is held in a 400-seat auditorium. Each concert ticket sells for $10, and 85% of the tickets are sold. How much money does the band earn from the sale of the tickets?
Answer: $3 400
Explanation:
total money to be collected by selling 400 tickets @$10
400 x 10 = 4000
4000 x 85%
4000 x \(\frac{85}{100}\) = 3400
$3400 much money does the band earn from the sale of the tickets.