This handy Math in Focus Grade 7 Workbook Answer Key Chapter 8 Volume and Surface Area of Solids detailed solutions for the textbook questions.
Math in Focus Grade 7 Course 2 B Chapter 8 Answer Key Volume and Surface Area of Solids
Math in Focus Grade 7 Chapter 8 Quick Check Answer Key
Solve.
Question 1.
A cube has edges measuring 6 centimeters each.
a) Find its volume.
Answer: The volume of the cube V is 216 cm³
Explanation:
Given, the edge of a cube a = 6 cm each
Formula for volume of a cube V is a³
Here, a = 6
V = a³ = 6³
V = 6 × 6 × 6 = 216
So, The volume of the cube V is 216 cm³.
b) Find its surface area.
Answer: The surface area of the cube A is 216 cm²
Explanation:
Given, the edge of a cube a = 6 cm each
Formula for surface area of a cube A is 6a²
Here, a = 6
A = 6a² = 6 × 6²
A = 6 × 6 × 6 = 216 cm²
So, The surface area of the cube A is 216 cm².
Question 2.
The volume of a cube is 512 cubic centimeters. Find the length of each edge of the cube.
Answer: The length of each edge of the cube a is 8 cm
Explanation:
Given, the volume of a cube is 512 cubic centimeters.
Here, V = a³ = 512 cm³
a³ = 8× 8 × 8 = 512 cm³
Then, a = 8.
So, the length of each edge of the cube a is 8 cm
Question 3.
A pyramid has a square base measuring 10 inches on each side. It has four faces that are congruent isosceles triangles. The height of each triangle is 13 inches. Find the surface area of the pyramid.
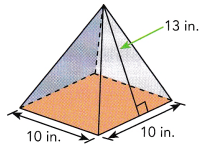
Answer: The total surface area of the pyramid is 360 in²
Explanation:
Given, The height of each triangle is 13 inches.
The pyramid has a square base measuring 10 inches on each side.
The area of each triangle is \(\frac{1}{2}\) × bh ,
Here, base b = 10 in. and height h = 13 in.
Area of each triangle = \(\frac{1}{2}\) × 10 × 13
Area of each triangle = 65 in²
There are total 4 triangles in the pyramid , so the area of 4 triangles are 4 × 65 = 260 in².
The area of a square is a² = 10² = 10 × 10 = 100 in²
So, The total surface area of a pyramid is 260 + 100 = 360 in².
Use 3.14 as an approximation for π.
Question 4.
Shawn makes waffles for breakfast. Each waffle is a circle with a diameter of 6 inches.
a) Find the circumference of a waffle.
Answer: The circumference of a waffle is 18.85 in.
Explanation:
Given, Each waffle is a circle with a diameter of 6 inches
We know that radius r = \(\frac{d}{2}\)
Here, d = 6
then, r = \(\frac{6}{2}\) = 3,
The circumference of a circle is C = 2πr
C = 2 × π × 3 , let us take π = 3.14,
C = 6.28 × 3 = 18.85
So, The circumference of a waffle is C = 18.85 in.
b) Find the area of the waffle.
Answer: The area of the waffle is 28.27 in²
Explanation:
Here r = 3 in.
The area of a circle is A = πr², let us take π = 3.14,
A = 3.14 × 3 × 3 = 28.27
So, The area of the waffle is 28.27 in²
Question 5.
The circumference of a wheel is 320.28 centimeters.
a) Find the radius of the wheel.
Answer: The radius of the wheel is 51 cm
Explanation:
Given, The circumference of a wheel is 320.28 centimeters.
We know that the circumference of a circle is π d
Where d is the diameter of the circle
then, π d = 320.28
d = \(\frac{320.28}{ π}\) , take π = 3.14
= \(\frac{320.28}{ 3.14}\)
d = 102,
d = 2r or r = \(\frac{d}{2}\)
r = \(\frac{102}{2}\)
r = 51 cm.
So, The radius of the wheel is 51 cm
b) Find the area of the wheel.
Answer: The area of the wheel is 8167.14 cm²
Explanation:
Here r = 51 cm
The area of a circle is A = πr², let us take π = 3.14,
A = 3.14 × 51 × 51
= 3.14 × 2601
A = 8167.14
So, The area of the wheel is 8167.14 cm²
Match each solid to its net.
Question 6.
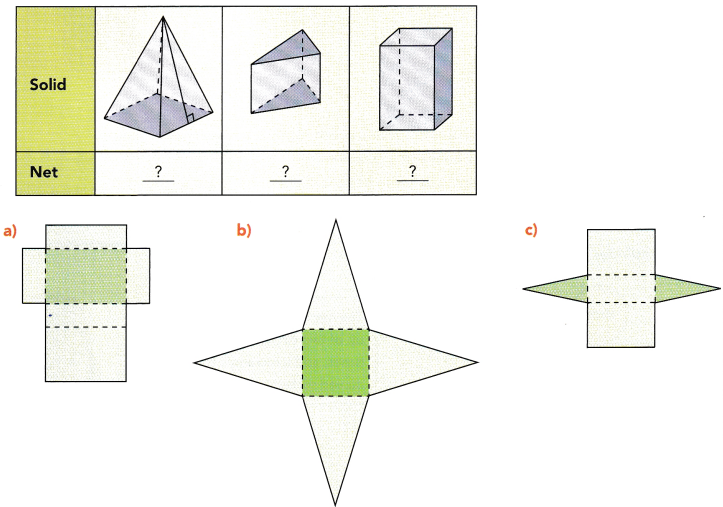
Answer: 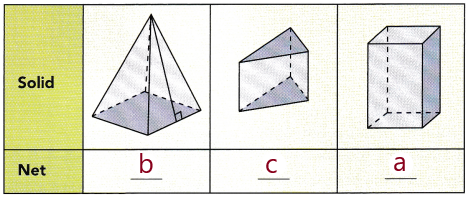
Explanation:
1. The first solid represents a pyramid with a square base and four triangles having a height perpendicular to the base.
2. The second solid represents a triangular prism .
3. The third solid represents a cuboid.