This handy Math in Focus Grade 7 Workbook Answer Key Chapter 8 Lesson 8.1 Recognizing Cylinders, Cones, Spheres, and Pyramids detailed solutions for the textbook questions.
Math in Focus Grade 7 Course 2 B Chapter 8 Lesson 8.1 Answer Key Recognizing Cylinders, Cones, Spheres, and Pyramids
Hands-On Activity
Materials:
- clay
- string
FIND THE SHAPE OF CROSS SECTIONS OF SOLIDS
Work in pairs.
STEP 1: Make three clay cubes. Use the string to slice a cube vertically so that the cross section is parallel to one face, as shown. Sketch the cross section and describe its shape.
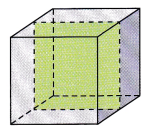
STEP 2: Use a string to slice another cube diagonally, as shown. Sketch the cross section and describe its shape.
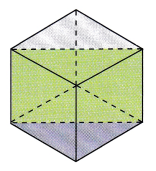
STEP 3: Use a string to slice the last cube through the midpoints of each of three edges that share a common vertex, as shown. Sketch the cross section and describe its shape.
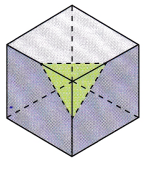
Math Journal Are you able to slice a cube in other ways to form the cross-section in STEP 1 to STEP 3?
Answer:
Math in Focus Grade 7 Chapter 8 Lesson 8.1 Guided Practice Answer Key
For each solid, name the shape of the cross-section formed when the solid is sliced by the plane shown.
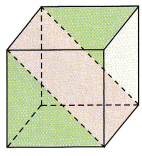
Question 1.
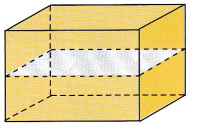
Answer: Rectangle
Explanation:
The shape of the cross-section formed when the solid is sliced by the plane is a Rectangle.
Because, It forms a closed figure having four sides of which two of the opposite sides are equal.
So, it forms a Rectangle.
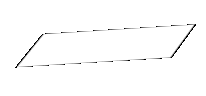
Question 2.
Answer: Rectangle
Explanation:
The shape of the cross-section formed when the solid is sliced by the plane is a Rectangle.
Because, It forms a closed figure having four sides of which two of the opposite sides are equal.
So, it forms a Rectangle.
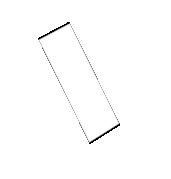
Question 3.
Answer: Square
Explanation:
The shape of the cross-section formed when the solid is sliced by the plane is a Square.
Because, It forms a closed figure having four sides of which all the sides are equal.
So, it forms a Square
Question 4.
Answer: Triangle
Explanation:
The shape of the cross-section formed when the solid is sliced by the plane is a Triangle.
Because, It forms a closed figure having three sides .
So, it forms a Triangle.
Math in Focus Course 2B Practice 8.1 Answer Key
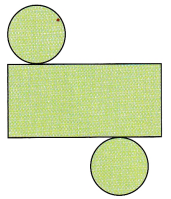
Match each set to its net.
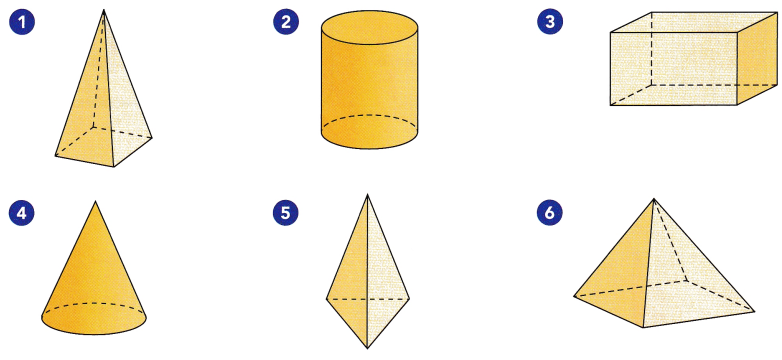
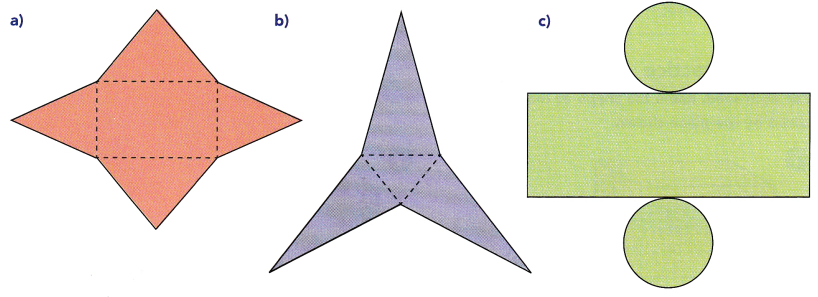
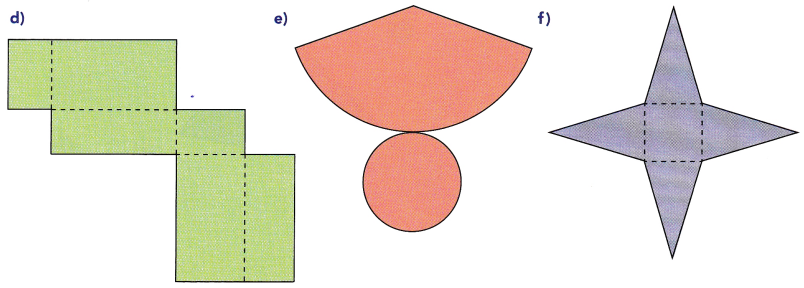
Answer: The combinations of the figures are
1- f
2- c
3- d
4- e
5- b
6- a
Name the solid that can be formed from each net.
Question 7.
Answer: The closed figure formed is a cylinder
Explanation:
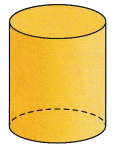
It forms a cylinder
Question 8.
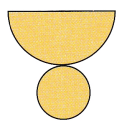
Answer: The closed figure formed is a cylinder
Explanation:

It is a cylinder.
Question 9.
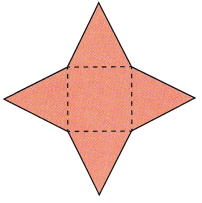
Answer: The closed figure formed is a Square pyramid
Explanation:
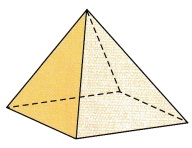
It is a square pyramid
Question 10.

Answer: The closed figure formed is a Triangular prism
Explanation:
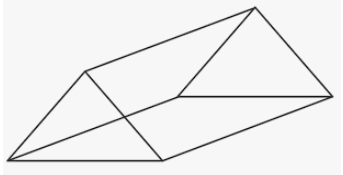
It is a triangular prism.
Solve. Show your work.
Question 11.
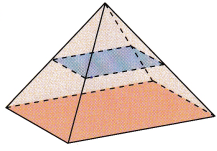
Tell what cross-section is formed when a plane slices a square pyramid as described.
a) Perpendicular to its base and passes through its vertex.
Answer: The figure Perpendicular to its base and passes through its vertex is a triangle
Explanation:
Thee square pyramid is
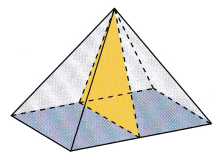

So, The figure Perpendicular to its base and passes through its vertex is a triangle
b) Parallel to its base.
Answer: The figure parallel to its base is a square
Explanation:
The square pyramid is
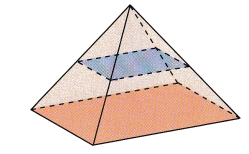

So, The figure parallel to its base is a square.
Question 12.
The diagram shows a cone and its net.
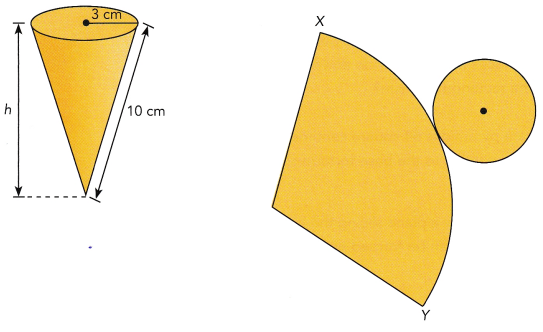
a) Copy the net of the cone and label these dimensions on the net.
Answer:
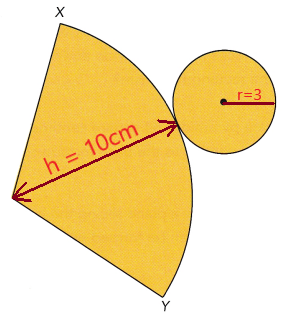
b) How is the circumference of the base of the cone related to the curve XV?
Answer: The closed figure of the net forms a cone and its is a circle
Explanation:
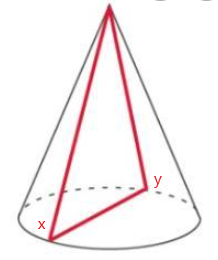
Given,, the radius of a circle is 3 cm
From that the circumference of a circle is 2πr
C = 2 (3.14)(3) = 18.84 cm
So, The xy becomes the circumference of a circle .
Question 13.
The diagram shows the net of a cylinder. Which sides of the rectangle have the same length as the circumference of the circular base?
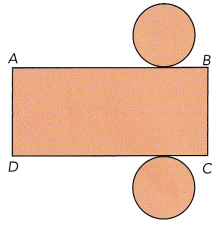
Answer: The sides of the rectangle have the same length as the circumference of the circular base are AB and DC
Explanation:
The closed figure of this net becomes a cylinder

So, The sides of the rectangle have the same length as the circumference of the circular base are AB and DC.
Question 14.
A base of each of the following prism is shaded. Name the shape of the cross section formed when each prism is sliced by a plane parallel to each base. Copy each prism. Sketch the cross sections and label them with the dimensions.
a)
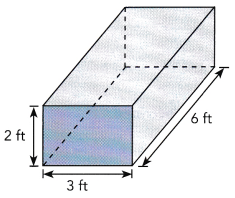
Answer:
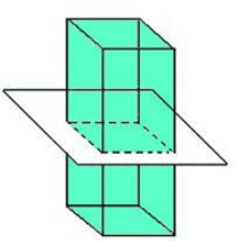
b)
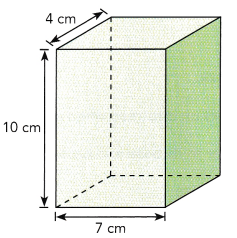
Answer:
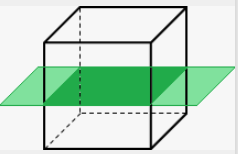
Question 15.
A cross-section that is parallel to one of the bases of a rectangular prism is 3 inches wide and 6 inches long. A cross-section that is perpendicular to its bases and parallel to two other faces is 4 inches wide and 6 inches long. What are the dimensions of the rectangular prism?
Answer: The dimensions of a rectangular prism are
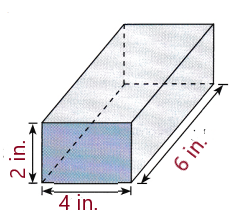
Question 16.
The area of the base of a square pyramid is 64 square centimeters. Several planes slice through the pyramid parallel to the base to form square cross-sections.
a) Besides the cross-section formed by a plane slicing the base, how many cross-sections parallel to the base can be formed with areas that are perfect squares?
Answer: There can be 7 perfect squares after the multiple cross section.
Explanation:
The area of the base of a square pyramid is 64 square centimeters
That is a = 8 , Area a² = 8 × 8 = 64
So, cross-sections parallel to the base can be formed with areas that are perfect squares are
If a = 7 , a² = 7 × 7 = 49,
If a = 6 , a² = 6 × 6 = 36,
If a = 5 , a² = 5 × 5 = 25,
If a = 4 , a² = 4 × 4 = 16,
If a = 3 , a² = 3 × 3 = 9,
If a = 2 , a² = 2 × 2 = 4,
If a = , a² = 1 × 1 = 1,
There can be 7 perfect squares after the multiple cross section.
b) Find the sum of the area of the base and the areas of the cross-sections found in a).
Answer: The sum of the area of the base is 28 cm²
The sum of the area of the cross-sections is 140 cm²