This handy Math in Focus Grade 7 Workbook Answer Key Chapter 8 Lesson 8.2 Finding Volume and Surface Area of Cylinders detailed solutions for the textbook questions.
Math in Focus Grade 7 Course 2 B Chapter 8 Lesson 8.2 Answer Key Finding Volume and Surface Area of Cylinders
Math in Focus Grade 7 Chapter 8 Lesson 8.2 Guided Practice Answer Key
Use the given dimensions to find the volume of each cylinder. Use 3.14 as an approximation for π. Round your answer to the nearest tenth.
Question 1.
Radius = 5 cm, Height = 7.5 cm
Answer: The volume of the cylinder is 588.75 cm³
Explanation:
We know that , the volume of the cylinder V = πr²h
Here r = 5 cm , h = 7.5 cm,
V = πr²h
= 3.14 × (5)² × 7.5
= 5.8875 cm³
So, The volume of the cylinder is 588.75 cm³
Question 2.
Diameter = 7 in., Height = 5 in.
Answer: The volume of the cylinder is 192.3 in³
Explanation:
We know that , the volume of the cylinder V = πr²h
Here d = 7 in , h = 5 in,
then, r = 3.5
V = πr²h
= 3.14 × (3.5)² × 5
= 192.3 cm³
So, The volume of the cylinder is 192.3 cm³
Complete. Use 3.14 as an approximation for π.
Question 3.
The volume of a cylindrical tank of water is 1,808.64 cubic meters. The radius is 12 meters. What is the height of the cylindrical tank?
Use the formula for volume to find the height, h, of the cylinder.
The height of the cylindrical tank is about ![]() meters.
meters.
Answer: The height of the cylindrical tank is about 4 meters.
Explanation:
Given, the volume of the tank V = 1,808.64 cubic meters, radius r = 12 meters
We know that , the volume of the cylinder V = πr²h
here π = 3.14
V = πr²h
h = \(\frac{V}{πr²}\)
= \(\frac{1808.64}{3.14 × 12 × 12}\)
= \(\frac{1808.64}{452.16}\)
= 4
So, The height of the cylindrical tank is about 4 meters.
Hands-On Activity
Materials:
- a tin can or any other cylindrical object
- paper
- scissors
Work in pairs.
STEP 1: What is the shape of the bases of your cylinder?
Write an expression for the area of one base in terms of r.
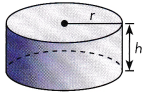
STEP 2: Cut a piece of paper to cover the curved surface of the cylinder. One end of the paper should meet the other end without overlapping.
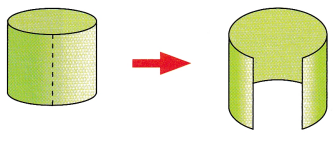
STEP 3: Lay the paper flat on the table to form a rectangle. Use the information below to write expressions for its length and width in terms of r and h.
Length of rectangle = Circumference of the base = ![]()
Width of rectangle = Height of cylinder = ![]()
Now write an expression for the area of the curved surface in terms of rand h.
STEP 4: Use the expressions written in STEP 1 and STEP 3 to write an expression for the surface area of a cylinder.
Surface area = Area of bases + Area of curved surface
Solve. Use 3.14 as an approximation for π. Round to the nearest tenth.
Question 4.
A cylinder has a radius of 4 inches and a height of 7 inches. Find the surface area of the cylinder.
Answer: The surface area of the cylinder is 276 in².
Explanation:
The formula for the surface area of the cylinder A = 2πrh + 2πr²
Here r = 4 in. , h = 7 in. ,
A = (2 × 3.14 × 4 × 7) + ( 2 × 3.14 × 4 × 4)
= 175.84 + 100.48
= 276.32 in²
≈ 276 in²
So, The surface area of the cylinder is 276 in².
Solve.
Question 5.
The area of the curved surface of a cylindrical can is l62π square centimeters and its height is 9 centimeters. What is the diameter of the can?
Area of curved surface = 2πrh Use the formula for the area of the curved surface.
![]() = 2πr •
= 2πr • ![]() Substitute the surface area and height.
Substitute the surface area and height.
![]() = 2 •
= 2 • ![]() • πr Multiply 2 by
• πr Multiply 2 by ![]()
![]() =
= ![]() Simplify.
Simplify.
\(\frac{?}{?}=\frac{?}{?}\) Divide both sides by ![]() .
.
![]() = r Simplify.
= r Simplify.
The diameter of the can is ![]() centimeters.
centimeters.
Answer: The diameter of the can is 18 cm
Explanation:
Given, The area of the curved surface of a cylindrical can is l62π square centimeters and h = 9 cm,
We know that Area of curved surface = 2πrh
Now equate the given data to the area formula we get,
2πrh = l62π
2 × r × 9 = 162
r = \(\frac{162}{18}\)
r = 9 cm
Then, d = 2r = 2 × 9 = 18cm,
So, The diameter of the can is 18cm
Math in Focus Course 2B Practice 8.2 Answer Key
For this practice, you may use a calculator. Use 3.14 as an approximation for π. Round your answers to the nearest tenth when you can.
Find the volume of each cylinder.
Question 1.
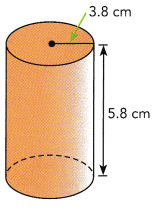
Answer: The volume of the cylinder is 263 cm³
Explanation:
We know that , the volume of the cylinder V = πr²h
Here r = 3.8 cm , h = 5.8 cm,
V = πr²h
= 3.14 × (3.8)² × 5.8
= 3.14 × 83.75
= 262.98 cm³
≈ 263 cm³
So, The volume of the cylinder is 263 cm³
Question 2.
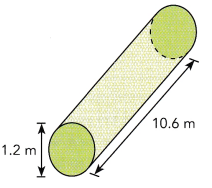
Answer: The volume of the cylinder is 12 m³
Explanation:
We know that , the volume of the cylinder V = πr²h
Here d = 1.2 m , h = 10.6 m,
then, r = 0.6 m
Because r = \(\frac{d}{2}\):
V = πr²h
= 3.14 × (0.6)² × 10.6
= 3.14 × 3.816
= 11.98 m³
≈ 12 m³
So, The volume of the cylinder is 12 m³
Solve.
Question 3.
A cylinder has a radius of 6 centimeters and a height of 28 centimeters. What is the volume?
Answer: The volume of the cylinder is 3165 cm³
Explanation:
We know that , the volume of the cylinder V = πr²h
Here r = 6 cm , h = 28 cm,
V = πr²h
= 3.14 × (6)² × 28
= 3.14 × 1008
= 3165.12 cm³
≈ 3165 cm³
So, The volume of the cylinder is 3165 cm³
Question 4.
A cylinder has a volume of 239 cubic centimeters and a height of 6 centimeters. What is the radius?
Answer: The radius of the cylinder is 3.5cm
Explanation:
We know that , the volume of the cylinder V = πr²h
Here v = 239 cm³ , h = 6 cm,
V = πr²h
r² = \(\frac{V}{πh}\)
= \(\frac{239}{3.14 × 6}\)
r²= 12.68
r = 3.56
≈ 3.5 cm
So, The radius of the cylinder is 3.5cm
Question 5.
Jenny is making a cylindrical pencil holder in shop class. It will be 14 centimeters high and 8 centimeters across. The bottom and sides of the container will be made of metal.
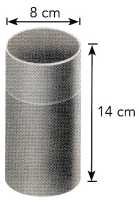
a) What is the area of the base?
Answer: The area of the base is 100.48 cm²
Explanation:
The area of the base = 2πr²
Given, d = 8cm,
Then r = 4 cm
2πr² = 2 × 3.14 × 4 × 4
= 100.48 cm²
So, The area of the base is 100.48 cm²
b) What is the area of the curved surface of the pencil holder?
Answer: The Area of curved surface is 351.68 cm²
Explanation:
We know that Area of curved surface = 2πrh
Here, h = 14 cm , r = 4 cm
2πrh = 2 × 3.14 × 4 × 14
= 351.68 cm²
So, The Area of curved surface is 351.68 cm²
c) What is the total surface area of the pencil holder?
Answer: The total surface area of the pencil holder is 452 cm².
Explanation:
The formula for the total surface area of the cylinder A = 2πrh + 2πr²
Here r = 4 cm, h = 14 cm ,
A = (2 × 3.14 × 4 × 14) + ( 2 × 3.14 × 4 × 4)
= 351.68 + 100.48
= 452.16 cm²
≈ 452 cm²
So, The total surface area of the pencil holder is 452 cm².
Question 6.
You want to make a tube with a height of 8 inches and a radius of 5 inches out of cardboard. The tube will be open at both ends. How much cardboard will you need to make the tube?
Answer: The cardboard needed to make the tube will be 753 in.
Explanation:
Given, h = 8 in. , r = 5 in.
cardboard needed to make the tube will be the curved surface area of the tube,
The Area of curved surface = 2πrh
2πrh = 2 × 3.14 × 8 × 15
= 753.6 in²
So, The Area of curved surface is 753 in².
Question 7.
The volume of a soup can is 125.6 cubic inches. The diameter of the can is 8 inches. What is the height of the soup can?

Answer: The height of the can is about 2.5inches .
Explanation:
Given, the volume of a soup can V = 125.6 cubic in., diameter of the can is 8 in.
Then, r = 4 in.,
We know that , the volume of the cylinder V = πr²h
here π = 3.14
V = πr²h
h = \(\frac{V}{πr²}\)
= \(\frac{125.6}{3.14 × 4 × 4}\)
= \(\frac{125.6}{50.24}\)
= 2.5 in.
So, The height of the can is about 2.5inches .
Question 8.
Mrs. Lavender bought a cylindrical lampshade with height 14 inches and diameter-10 inches. As shown in the diagram, the lampshade is open at the top and bottom. Find the surface area of the lampshade.
Answer: the surface area of the lampshade is 439 in²
Explanation:
We know that Area of curved surface = 2πrh
Here, h = 14 in , d = 10 in.,
Then r = 5 in,
2πrh = 2 × 3.14 × 5 × 14
= 439.6 in²
So, The Area of curved surface is 439 in².
Question 9.
The volume of a cylinder is 121 π cubic inches and its height is 4 inches.

a) What is the radius of the cylinder?
Answer: The radius of the cylinder is 5 in.
Explanation:
We know that , the volume of the cylinder V = πr²h
Here v = 121 π cubic inches , h = 4 inches.
V = πr²h
r² = \(\frac{V}{πh}\)
= \(\frac{121 × 3.14}{3.14 × 4}\)
r²= 30.25
r = 5.5
≈ 5 in
So, The radius of the cylinder is 5 in.
b) What is the surface area of the cylinder? Give your answer in terms of π.
Answer: the surface area of the cylinder is 40π in².
Explanation:
We know that Area of curved surface = 2πrh
Here, h = 4 in , r = 5 in
2πrh = 2 × π × 4 × 5
= 40π in²
So, The Area of curved surface is 40π in².
Question 10.
The diagram shows a mallet made by attaching two solid cylinders together. What is the volume of the mallet?
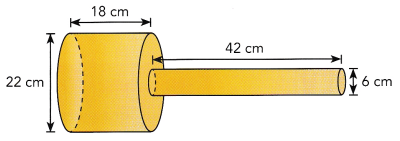
Answer: The volume of the mallet is V = 8024 cm³.
Explanation:
We know that , the volume of the cylinder V = πr²h
The volume of first cylinder is
Here d = 22 cm , h = 18cm,
then, r = 11 cm
V = πr²h
= 3.14 × (11)² × 18
= 6838.92 cm³
So, The volume of the first cylinder is 6838 cm³
The volume of second cylinder is
Here d = 6 cm , h = 42 cm,
then, r = 3 cm
V = πr²h
= 3.14 × (3)² × 42
= 1186.92 cm³
So, The volume of the second cylinder is 1186 cm³
Then, The volume of the mallet is volume of first cylinder + volume of second cylinder
= 6836 + 1186
V = 8024 cm³.
So, The volume of the mallet is V = 8024 cm³.
Question 11.
A company makes cylindrical cans for peaches. Each can has a radius of 4 centimeters and a height of 12 centimeters. The company plans to increase the volume of each can by 25%.
a) What will be the height of the new can if the radius remains the same?
Answer: The height of the new can is about 15 cm
Explanation:
We know that , the volume of the cylinder V = πr²h
Here r = 4 cm , h =12 cm,
V = πr²h
= 3.14 × (4)² × 12
= 602.88 cm³
So, The volume of the cylinder is 602 cm³
Given, increase the volume of each can by 25%.
The 25% of 602 = 150
Then V = 602 + 150 = 752 cm³
The new volume of the can is 752 cm³,
the height of the new can if the radius remains the same will be
V = πr²h
h = \(\frac{V}{πr²}\)
= \(\frac{752}{3.14 × 4 × 4}\)
= \(\frac{752}{50.24}\)
= 14.9 cm.
So, The height of the new can is about 15 cm .
b) What will be the radius of the new can if the height remains the same?
Answer: The radius of the new can is 4 cm.
Explanation:
The new volume of the can is 752 cm³,
the radius of the new can if the height remains the same will be
V = πr²h
r² = \(\frac{V}{πh}\)
= \(\frac{752}{3.14 × 12}\)
r²= 19.95
r = 4.4
≈ 4 cm
So, The radius of the new can is 4 cm
Question 12.
A cylindrical water tank has a radius of 5 feet and a height of 10 feet. The volume of water in the tank is 565.2 cubic feet.
a) What is the height of the water in the tank?
Answer: The height of the water in the tank is 7.2 feet.
Explanation:
Given, V = 565.2 cubic feet, r = 5 feet
We know that , the volume of the cylinder V = πr²h
here π = 3.14
V = πr²h
h = \(\frac{V}{πr²}\)
= \(\frac{565.2}{3.14 × 5 × 5}\)
= \(\frac{565.2}{78.5}\)
= 7.2 feet.
So, The height of the water in the tank is 7.2 feet.
b) What percent of the tank’s volume is filled with water?
Answer: The percent of the tank’s volume is filled with water is 72%
Explanation:
The height of the tank is 10 feet and
the height of the water in the tank is 7.2 feet
Then, 7.2 is 72% of 10
So, The percent of the tank’s volume is filled with water is 72%
Question 13.
Eric is painting 8 wooden cylinders. Each cylinder has a radius of 6.2 inches and a height of 12.4 inches. Eric can paint 50 square inches of wood using one pint of paint. How much paint will Eric need to paint all the wooden cylinders?
Answer: The paint will Eric need to paint all the wooden cylinders is 4 liters
Explanation:
Given, Eric is painting 8 wooden cylinders.
Each cylinder has a radius of 6.2 inches and a height of 12.4 inches.
Eric can paint 50 square inches of wood using one pint of paint.
= 8 × 50
= 400 in²
The paint will Eric need to paint all the wooden cylinders is 4 liters
Question 14.
The area of the curved surface of a cylindrical jar is 1,584 square centimeters. The height of the jar is 28 centimeters.
a) What is the circumference of the jar?
Answer: The circumference of the jar is 175 cm
Explanation:
Given, The area of the curved surface of a cylindrical jar is1 584 square centimeters and h = 28 cm,
We know that Area of curved surface = 2πrh
Now equate the given data to the area formula we get,
2πrh = 1584
2 × r × 28 = 1584
r = \(\frac{1584}{2 × 28}\)
r =28.28 cm
Then, d = 2r = 2 × 28 = 56 cm,
So, The diameter of the jar is 56cm
Circumference of the jar is C = πd
C = 3.14 × 56 = 175.84 cm
So, The circumference of the jar is 175 cm
b) What is the radius of the jar?
Answer: The radius of the jar is 28.28 cm
Explanation:
Given, The area of the curved surface of a cylindrical jar is1 584 square centimeters and h = 28 cm,
We know that Area of curved surface = 2πrh
Now equate the given data to the area formula we get,
2πrh = 1584
2 × r × 28 = 1584
r = \(\frac{1584}{2 × 28}\)
r =28.28 cm
So, The radius of the jar is 28.28 cm.
Question 15.
Math journal Joyce uses the formula 5 = 2πr(r + h) to find the surface area of a cylinder. Assuming she uses the correct values for r and h, will she get the correct volume? Explain your thinking.
Answer: Yes, she will get the correct volume.
Explanation:
We know that , Surface area = Area of bases + Area of curved surface
She used the formulas 2πrh + 2πr²
the volume of the cylinder V = πr²h
she uses the correct values for r and h
So, yes she will get the correct volume.