This handy Math in Focus Grade 5 Workbook Answer Key Chapter 15 Practice 3 Nets and Surface Area provides detailed solutions for the textbook questions.
Math in Focus Grade 5 Chapter 15 Practice 3 Answer Key Nets and Surface Area
Find the surface area of each cube.
Example
3 × 3 = 9
6 × 9 = 54
Surface area of cube = 54 cm2
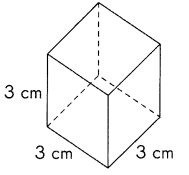
Question 1.
Answer:
S.A = 150 in.2,
Explanation:
As we know surface area (S.A) of cube is 6 X (side X side),
Given cube has 5 in side therefore S.A = 6 X (5 in X 5 in) =
6 X (25 in.2) = 150 in.2.
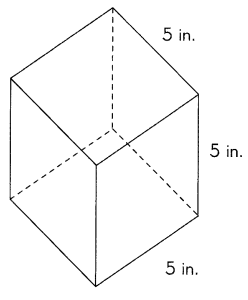
Question 2.
Answer:
S.A = 864 in.2,
Explanation:
As we know surface area (S.A) of cube is 6 X (side X side),
Given cube has 12 in side therefore S.A = 6 X (12 in X 12 in) =
6 X (144 in.2) = 864 in.2.
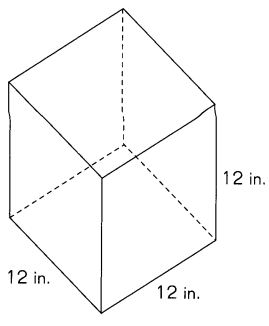
Question 3.
Answer:
S.A = 1924 cm2,
Explanation:
As we know surface area (S.A) of cube is 6 X (side X side),
Given cube has 18 in side therefore S.A = 6 X (18 cm X 18 cm) =
6 X (324 cm2) = 1924 cm2.
Find the surface area of each rectangular prism.
Example
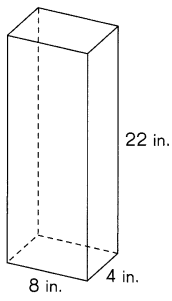
2 × 8 × 4 = 64
2 × 22 × 4 = 176
2 × 22 × 8= 352
64 + 176 + 352 = 592
Surface area of rectangular prism = 592 in.2
Question 4.
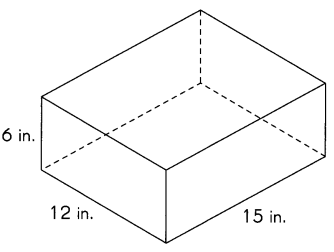
Answer:
The surface area of rectangular prism is 684 in.2,
Explanation:
As the surface area of rectangular prism is
2 X [(width X length) + (height X length) + (height X width)],
= 2 X [(12 in X 15 in) + (6 in X 15 in) + (6 in X 12 in)],
= 2 X [(180 in.2) + (90 in.2) + (72 in.2)]
= 2 X [ 342 in.2],
= 684 in.2.
Question 5.
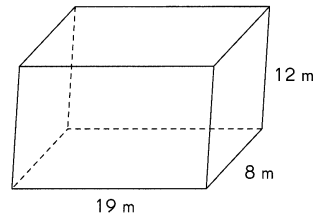
Answer:
The surface area of rectangular prism is 952 m.2,
Explanation:
As the surface area of rectangular prism is
2 X [(width X length) + (height X length) + (height X width)],
= 2 X [(8 m X 19 m) + (12 m X 19 m) + ( 12 m X 8 m)],
= 2 X [(152 m.2) + (228 m.2) + (96 m.2)]
= 2 X [ 476 m.2],
= 952 m.2.
Find the surface area of each triangular prism.
Example
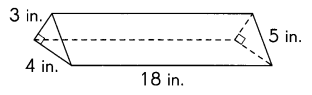
Answer:
Surface area of triangular prism = 228 in.2
Explanation:
2 × \(\frac{1}{2}\) × 3 in × 4 in = 12 in.2
4 in × 18 in = 72 in.2
3 in × 18 in = 54 in.2
5 in × 18 in = 90 in.2
12 in.2+ 72 in.2 + 54 in.2 + 90 in.2 = 228 in.2
Surface area of triangular prism = 228 in.2
Question 6.
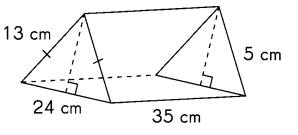
Answer:
Explanation:
The formula for the surface area of triangular prism is:
Surface area = bh + (l X w + w X h + l X h),
= (5 cm X 35 cm) + (13 cm X 24 cm + 24 cm X 5 cm + 13 cm X 35 cm),
= 175 cm2+ ( 312 cm2+ 120 cm2+ 455 cm2)
= 1,062 cm2.
Solve. Show your work.
Question 7.
Jeffrey cuts out the net of a box he wants to make.
Find the surface area of the box.
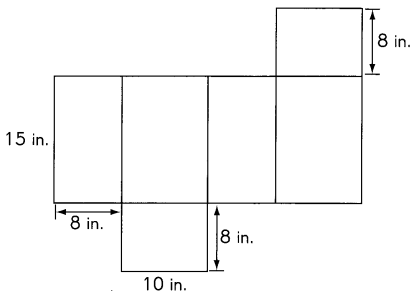
Answer:
The surface area of Jeffrey box is 684 in.2,
Explanation:
Jeffrey box contains 1 square of 8 in side,
2 rectangles of length 15 in and 8 in width,
2 rectangles of length 15 in and 10 in width,
1 rectangle of length 10 in and 8 in width,
So the surface area of Jeffrey box is
8 in X 8 in = 64 in.2
2 X (15 in X 8 in) = 2 X 120 in.2= 240 in.2
2 X (15 in X 10 in) = 2 X 150 in.2= 300 in.2
1 X (10 in X 8 in) = 80 in.2
surface area = 64 in.2+ 240 in.2 + 300 in.2+ 80 in.2,
surface area = 684 in.2.
Solve. Show your work.
Question 8.
This glass fish tank does not have a cover. Find the total area of the
glass panels used to make the tank.
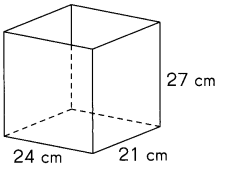
Answer:
The total area of the glass panels used to make the tank is = 288 cm2,
Explanation:
Given glass fish tank that does not have a cover. The total area of the
glass panels used is in the shape of cuboid,
therefore to make the tank we need
2(lw + lh + hw) = 2 X [(24 cm + 21 cm) + (24 cm + 27 cm) + (27 cm + 21 cm)],
= 2 X (45 cm2 + 51 cm2 + 48 cm2),
= 2 X (144 cm2),
= 288 cm2.
Question 9.
The tank shown is made of steel. It does not have a cover.
Find the area of steel sheet used to make the tank.
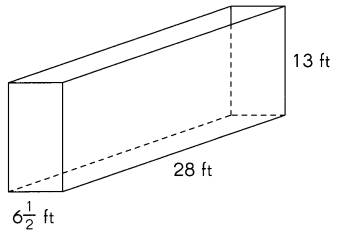
Answer:
The total area of the steel sheet is 190 ft2,
Explanation:
Given tank shown is made of steel,
The total area of the steel sheet used is in the shape of rectangular prism,
therefore to make the tank we need
2(lw + lh + hw) = 2 X [(6 1/2 ft + 28 ft) + (6 1/2 ft + 13 ft) + (13 ft + 28 ft)],
= 2 X (34 1/2 ft2 + 19 1/2 ft2 + 41 ft2),
= 2 X (95 ft2),
= 190 ft2.
Question 10.
A rectangular piece of poster board measures 60 centimeters by 80 centimeters.
Linn draws the net of a box on the poster board and cuts it out.
If the box measures 10 centimeters by 16 centimeters by 27 centimeters,
what is the area of the poster board left?
Answer:
The area of the poster board left 3076 cm2,
Explanation:
Given a rectangular piece of poster board measures 60 centimeters by 80 centimeters.
Area of poster board is 60 cm X 80 cm = 4800 cm2.
Linn draws the net of a box on the poster board and cuts it out.
If the box measures 10 centimeters by 16 centimeters by 27 centimeters,
the surface area of the box is
2(lw + lh + hw) = 2 X [(10 cm + 16 cm) + (16 cm + 27 cm) + (27 cm + 10 cm)],
= 2 X (160 cm2 + 432 cm2 + 270 cm2),
= 2 X (862 cm2),
= 1724 cm2,
therefore 4800 cm2– 1724 cm2 = 3076 cm2.