Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 9 Lesson 9.1 Points on the Coordinate Plane to score better marks in the exam.
Math in Focus Grade 6 Course 1 B Chapter 9 Lesson 9.1 Answer Key Points on the Coordinate Plane
Math in Focus Grade 6 Chapter 9 Lesson 9.1 Guided Practice Answer Key
Use the coordinate plane below.
Question 1.
Give the coordinates of points P, Q, R, S, T, U, and V. In which quadrant is each point located?
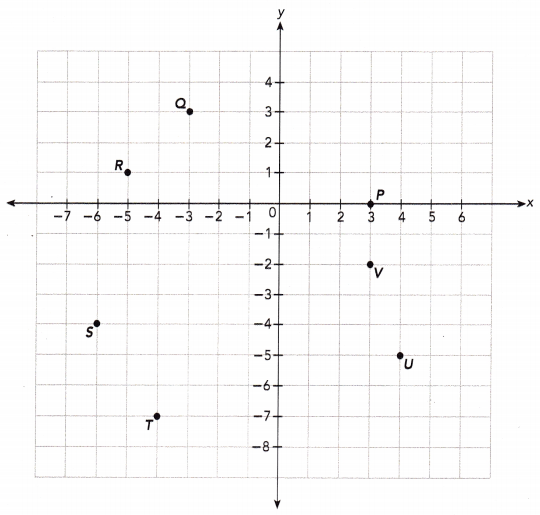
Answer:
Point P:
The first coordinate represents distance along x axis which is 3 and the second coordinate represents distance along y axis which is 0.
So, the point P will be (3,0).
The point having y-coordinate as 0 lie on the X-axis and thus is not located in any quadrant.
Point Q:
The first coordinate represents distance along x axis which is -3 and the second coordinate represents distance along y axis which is 3.
So, the point Q will be (-3,3).
If the x axis coordinate is negative and y axis coordinate is positive, the point will lie in quadrant II.
Point R:
The first coordinate represents distance along x axis which is -5 and the second coordinate represents distance along y axis which is 1.
So, the point R will be (-5,1).
If the x axis coordinate is negative and y axis coordinate is positive, the point will lie in quadrant II.
Point S:
The first coordinate represents distance along x axis which is -6 and the second coordinate represents distance along y axis which is -4.
So, the point S will be (-6,-4).
If the both the coordinates are negative then, the point will lie in quadrant III.
Point T:
The first coordinate represents distance along x axis which is -4 and the second coordinate represents distance along y axis which is -7.
So, the point T will be (-4,-7).
If the both the coordinates are negative then, the point will lie in quadrant III.
Point U:
The first coordinate represents distance along x axis which is 4 and the second coordinate represents distance along y axis which is -5.
So, the point U will be (4,-5).
If the x axis coordinate is positive and y axis coordinate is negative , the point will lie in quadrant IV.
Point V:
The first coordinate represents distance along x axis which is 3 and the second coordinate represents distance along y axis which is -2.
So, the point V will be (3,-2).
If the x axis coordinate is positive and y axis coordinate is negative , the point will lie in quadrant IV.
Use graph paper.
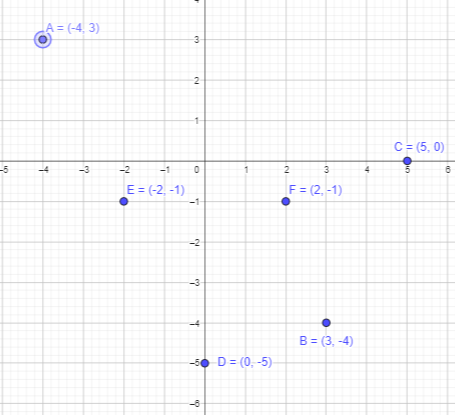
Question 2.
Plot points A (-4, 3), 6(3, -4), C (5, 0), D (0, -5), E(-2, -1), and F(2, -1)on a coordinate plane.
Answer:
To plot point A(-4,3):
Here, the x-coordinate of A is -4 and the y-coordinate is 3. Start at the Origin. As the x coordinate is negative, move 4 units to the left along the x-axis and 3 units to the top along y -axis.
Thus, the required point A(-4,3) is marked.
To plot point B(3,-4):
Here, the x-coordinate of B is 3 and the y-coordinate is -4. Start at the Origin. As the x coordinate is positive, move 3 units to the right along the x-axis. As y cooridnate is negative, move 4 units to the down along y -axis.
Thus, the required point B(-3,4) is marked.
To plot point C(5,0):
Here, the x-coordinate of C is 5 and the y-coordinate is 0. As the x coordinate is positive, move 5 units to the right along the x-axis and mark it. Thus, the required point(5,0) is marked.
To plot point D(0,-5):
Here, the x-coordinate of D is 0 and the y-coordinate is -5. As the y coordinate is negative, move 5 units to the down along the y-axis and mark it. Thus, the required point(0,-5) is marked.
To plot point E(-2, -1):
Here, the x-coordinate of E is -2 and the y-coordinate is -1. As the x coordinate is negative, move 2 units to the left along the x-axis. As the y coordinate is negative, move 1 units to the down along the y-axis and mark it.
Thus, the required point (-2,-1) is marked.
To plot point F(2, -1):
Here, the x-coordinate of E is 2 and the y-coordinate is -1. As the x coordinate is positive, move 2 units to the right along the x-axis. As the y coordinate is negative, move 1 units to the down along the y-axis and mark it.
Thus, the required point (2,-1) is marked.
Question 3.
Points P and Q are reflections of each other about the x-axis. Give the coordinates of point Q if the coordinates of point P are the following:
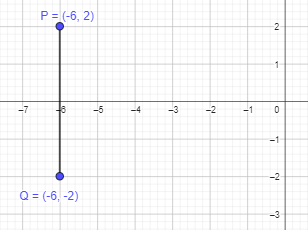
a) (-6, 2)
Answer:
Given that the points P and Q are reflections of each other about the x-axis.
Given that Q is reflection of point P in the x-axis and point P is (-6,2).
If a point is reflected across the x-axis, The x-coordinate remains the same, but the y-coordinate is taken to be the additive inverse.
Thus, x cordinate will be -6 and y coordinate will be -2.
Therefore, point Q will be (-6,-2).
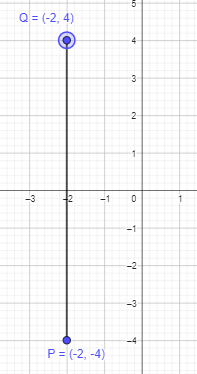
b) (-2, -4)
Answer:
Given that Q is reflection of point P in the x-axis and point P is (-2, -4).
If a point is reflected across the x-axis, The x-coordinate remains the same, but the y-coordinate is taken to be the additive inverse.
Thus, x cordinate will be -2 and y coordinate will be 4.
Therefore, point Q will be (-2,4).
c) (4, 5)
Answer:
Given that Q is reflection of point P in the x-axis and point P is (4, 5).
If a point is reflected across the x-axis, The x-coordinate remains the same, but the y-coordinate is taken to be the additive inverse.
Thus, x cordinate will be 4 and y coordinate will be -5.
Therefore, point Q will be (4,-5).
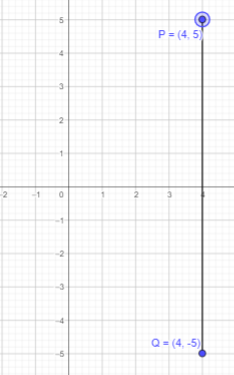
d) (7, -3)
Answer:
Given that Q is reflection of point P in the x-axis and point P is (7, -3).
If a point is reflected across the x-axis, The x-coordinate remains the same, but the y-coordinate is taken to be the additive inverse.
Thus, x cordinate will be 7 and y coordinate will be 3.
Therefore, point Q will be (7,3).
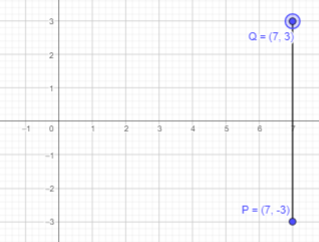
Question 4.
Points R and S are reflections of each other about the y-axis. Give the coordinates of point S if the coordinates of point R are the following:
a) (-6,2)
Answer:
Given that the points R and S are reflections of each other about the y-axis.
Given that R is reflection of point S in the y-axis and point R is (-6,2).
If a point is reflected across the y-axis, The x-coordinate is taken to be the additive inverse and the y-coordinate remains the same.
Thus, x cordinate will be 6 and y coordinate will be 2.
Therefore, point S will be (6,2).
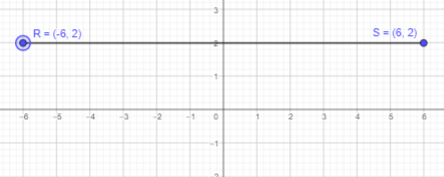
b) (-2, -4)
Answer:
Given that R is reflection of point S in the y-axis and point R is (-2, -4).
If a point is reflected across the y-axis, The x-coordinate is taken to be the additive inverse and the y-coordinate remains the same.
Thus, x cordinate will be 2 and y coordinate will be -4.
Therefore, point S will be (2,-4).
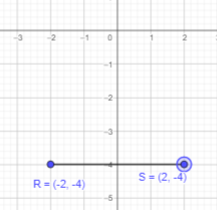
c) (4, 5)
Answer:
Given that R is reflection of point S in the y-axis and point R is (4, 5).
If a point is reflected across the y-axis, The x-coordinate is taken to be the additive inverse and the y-coordinate remains the same.
Thus, x cordinate will be -4 and y coordinate will be 5.
Therefore, point S will be (-4,5).
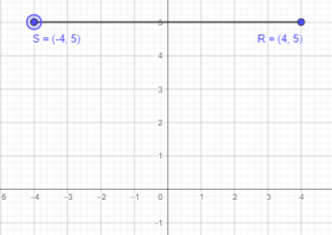
d) (7, -3)
Answer:
Given that R is reflection of point S in the y-axis and point R is (7, -3).
If a point is reflected across the y-axis, The x-coordinate is taken to be the additive inverse and the y-coordinate remains the same.
Thus, x cordinate will be -7 and y coordinate will be -3.
Therefore, point S will be (-7,-3).
Use graph paper. For each exercise, plot the given points on a coordinate plane. Then join the points in order with line segments to form a closed figure. Name each figure formed.
Question 5.
A (3, 4), B (-6, -3), and C (2, -4)
Answer:
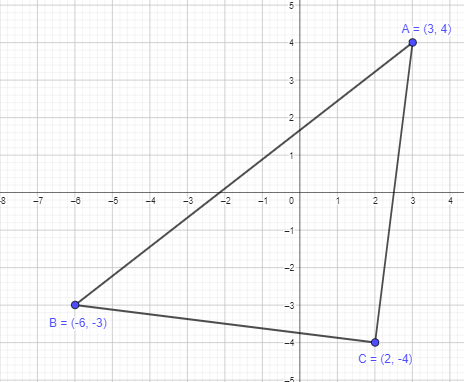
Given points are, A (3, 4), B (-6, -3), and C (2, -4).
To get a closed figure, plot the above points and join them in order.
It is forming a three-sided polygon, which is a triangle.
Thus, ABC will form a triangle as shown in the graph above.
Question 6.
D(1, 1), E(0, 0), and F (-4, 4)
Answer:
Given points are, D(1, 1), E(0, 0), and F (-4, 4).
To get a closed figure, plot the above points and join them in order.
It is forming a straight line.
Thus, DEF is a straight line as shown in the graph above.
Question 7.
J (-3, 0), K (0, 5), and L (3, 0)
Answer:
Given points are, J (-3, 0), K (0, 5), and L (3, 0).
To get a closed figure, plot the above points and join them in order.
It is forming a three-sided polygon, which is a triangle.
Thus, JKL will form a triangle as shown in the graph above.
Question 8.
P (3, 2), Q (-1, 2), R (-1, -2), and S (3, -2)
Answer:
Given points are, P (3, 2), Q (-1, 2), R (-1, -2), and S (3, -2).
To get a closed figure, plot the above points and join them in order.
It is forming a four-sided polygon. All the sides are equal in length. A square have all equal sides.
Thus, PQRS will form a square as shown in the graph above.
Question 9.
W(-3, 2), X (1, -2), Y(3, 0), and Z(-1, 4)
Answer:
Given points are, W(-3, 2), X (1, -2), Y(3, 0), and Z(-1, 4)
To get a closed figure, plot the above points and join them in order.
It is forming a four-sided polygon. The opposite sides are equal in length. A rectangle will have opposite sides equal.
Thus, WXYZ will form a rectangle as shown in the graph above.
Question 10.
A (-5, 2), B (-5, -1), C(-1, -1), and D(1, 2)
Answer:
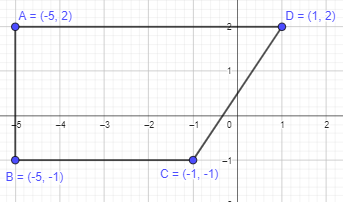
Given points are, A (-5, 2), B (-5, -1), C(-1, -1), and D(1, 2)
To get a closed figure, plot the above points and join them in order.
It is forming a four-sided polygon. All the four sides are of different length, and a pair of opposite sides seems to be parallel which can be a trapezuim.
Thus, ABCD will form a trapezium as shown in the graph above.
Question 11.
E (-2, -2), F (-5, -5), G (-2, -5), and H (1, -2)
Answer:
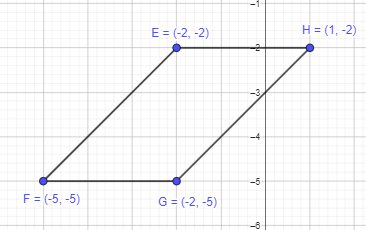
Given points are E (-2, -2), F (-5, -5), G (-2, -5), and H (1, -2)
To get a closed figure, plot the above points and join them in order.
It is forming a four-sided polygon. The opposite sides are parallel to each other. A parallelogram will have opposite sides in parallel.
Thus, EFGH will form a parallelogram as shown in the graph above.
Question 12.
J (-4, 1), K (-3, -1), L (0, -1), and M (2, 1)
Answer:
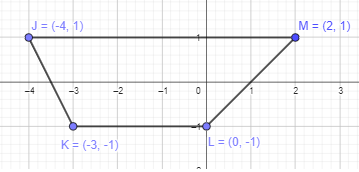
Given points are, J (-4, 1), K (-3, -1), L (0, -1), and M (2, 1)
To get a closed figure, plot the above points and join them in order.
It is forming a four-sided polygon. All the four sides are of different length, and a pair of opposite sides seems to be parallel which can be a trapezuim.
Thus, JKLM will form a trapezium as shown in the graph above.
Question 13.
P (4, 0), Q (0, 4), P (-4, 0), and S (0, -4)
Answer:
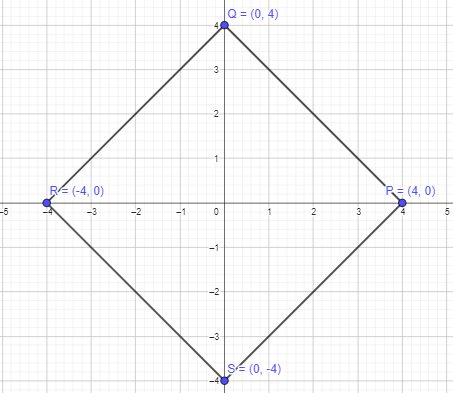
Given points are, P (4, 0), Q (0, 4), R (-4, 0), and S (0, -4)
To get a closed figure, plot the above points and join them in order.
It is forming a four-sided polygon. All the four sides are equal in length and diagonals are bisecting each other.
Thus, PQRS will form a rhombus.
Question 14.
W (-2, 0), X (-3, -3), Y(1, 1), and Z(2, 4)
Answer:
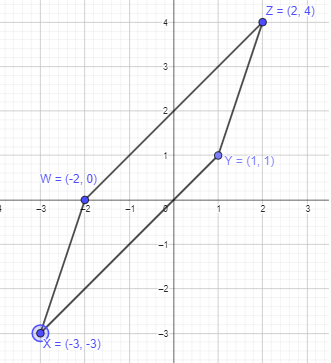
Given points are W (-2, 0), X (-3, -3), Y(1, 1), and Z(2, 4)
To get a closed figure, plot the above points and join them in order.
It is forming a four-sided polygon. The opposite sides are parallel to each other. A parallelogram will have opposite sides in parallel.
Thus, WXYZ will form a parallelogram as shown in the graph above.
Hands-On Activity
IDENTIFYING QUADRILATERALS DRAWN ON A COORDINATE PLANE
Work in pairs.
Step 1.
Plot four points on a coordinate plane and connect them to form a special quadrilateral such as a parallelogram, a rectangle, or a rhombus. Do not let your partner see your quadrilateral.
Step 2.
Tell your partner the coordinates of three out of the four coordinates of the points you plotted in Step 1. Also tell your partner the type of quadrilateral you plotted, and in which quadrant the fourth point is located. Have your partner guess the coordinates of the fourth point.
Example
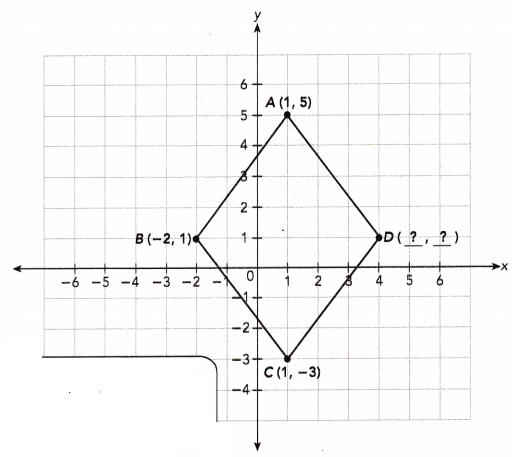
Points A (1, 5), B (-2, 1), C(1, -3), and D can be joined to form a rhombus. If point D is in Quadrant I, what are the coordinates of point D?
Step 3.
Switch roles with your partner and repeat the activity with other quadrilaterals.
Math in Focus Course 1B Practice 9.1 Answer Key
Use the coordinate plane below.
Question 1.
Give the coordinates of each point. In which quadrant is each point located?
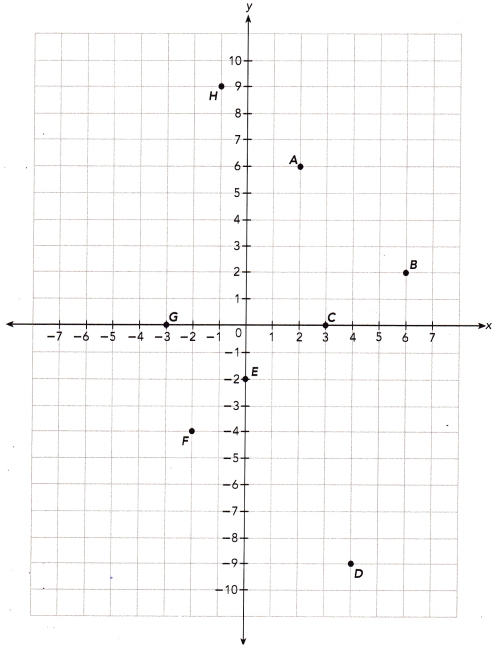
Answer:
Point A:
The first coordinate represents distance along x axis which is 2 and the second coordinate represents distance along y axis which is 6.
So, the point A will be (2,6).
If the x axis coordinate and y axis coordinate are positive, the point will lie in quadrant I.
Point B:
The first coordinate represents distance along x axis which is 6 and the second coordinate represents distance along y axis which is 2.
So, the point B will be (6,2).
If the x axis coordinate and y axis coordinate are positive, the point will lie in quadrant I.
Point C:
The first coordinate represents distance along x axis which is 3 and the second coordinate represents distance along y axis which is 0.
So, the point C will be (3,0).
The point having y-coordinate as 0 lie on the X-axis and thus is not located in any quadrant.
Point D:
The first coordinate represents distance along x axis which is 4 and the second coordinate represents distance along y axis which is 9.
So, the point D will be (4,-9).
If the x axis coordinate is positive and y axis coordinate is negative, then the point will lie in quadrant IV.
Point E:
The first coordinate represents distance along x axis which is 0 and the second coordinate represents distance along y axis which is 2.
So, the point E will be (0,-2).
The point having x-coordinate as 0 lie on the y-axis and thus is not located in any quadrant.
Point F:
The first coordinate represents distance along x axis which is 2 and the second coordinate represents distance along y axis which is 4.
So, the point F will be (-2,-4).
If the x axis coordinate and y axis coordinate are positive, the point will lie in quadrant III.
Point G:
The first coordinate represents distance along x axis which is 3 and the second coordinate represents distance along y axis which is 0.
So, the point G will be (-3,0).
The point having y-coordinate as 0 lie on the x-axis and thus is not located in any quadrant.
Point H:
The first coordinate represents distance along x axis which is 1 and the second coordinate represents distance along y axis which is 9.
So, the point F will be (-1,9).
If the x axis coordinate is negative and y axis coordinate is positive, than the point will lie in quadrant II.
Use graph paper. Plot the points on a coordinate plane. In which quadrant is each point located?
Question 2.
A (3, 7), B (2, 0), C (8, -1), D (0, -6), E(-3, -5), and F(-6, 7)
Answer:
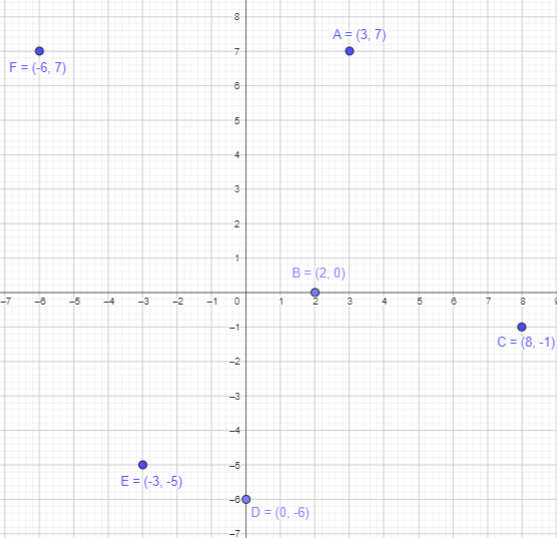
Point A (3, 7) lies in quadrant I, as x-coordinate and y-coordinate are both positive.
Point B (2, 0) is having y-coordinate as 0 lie on the x-axis does not lie in any quadrant.
Point C (8, -1) lies in quadrant IV, as x axis is positive and y-axis is negative.
Point D (0, -6) is having x-coordinate as 0 lie on the y-axis does not lie in any quadrant.
Point E (-3, -5) lies in quadrant III, as x-coordinate and y-coordinate are both negative.
Point F (-6, 7) lies in quadrant II, as x-coordinate is negative and y-coordinate is positive.
Use graph paper. Points A and B are reflections of each other about the x-axis. Give the coordinates of point B if the coordinates of point A are the following:
Question 3.
(4, 1)
Answer:
Given that the points A and B are reflections of each other about the x-axis.
Given that B is reflection of point A in the x-axis and point A is (4,1).
If a point is reflected across the x-axis, The x-coordinate remains the same, but the y-coordinate is taken to be the additive inverse.
Thus, x cordinate will be 4 and y coordinate will be -1.
Therefore, point B will be (4,-1).
Question 4.
(-2, 3)
Answer:
Given that B is reflection of point A in the x-axis and point A is (-2,3).
If a point is reflected across the x-axis, The x-coordinate remains the same, but the y-coordinate is taken to be the additive inverse.
Thus, x cordinate will be -2 and y coordinate will be -3.
Therefore, point B will be (-2,-3).
Question 5.
(2, -2)
Answer:
Given that B is reflection of point A in the x-axis and point A is (2,-2).
If a point is reflected across the x-axis, The x-coordinate remains the same, but the y-coordinate is taken to be the additive inverse.
Thus, x cordinate will be 2 and y coordinate will be 2.
Therefore, point B will be (2,2).
Question 6.
(-1, -3)
Answer:
Given that B is reflection of point A in the x-axis and point A is (-1,-3).
If a point is reflected across the x-axis, The x-coordinate remains the same, but the y-coordinate is taken to be the additive inverse.
Thus, x cordinate will be -1 and y coordinate will be 3.
Therefore, point B will be (-1,3).
Use graph paper. Points C and D are reflections of each other about the y-axis. Give the coordinates of point D if the coordinates of point C are the following:
Question 7.
(4, 1)
Answer:
Given that the points A and B are reflections of each other about the y-axis.
Given that B is reflection of point A in the x-axis and point A is (4,1).
If a point is reflected across the y-axis, The x-coordinate is taken to be the additive inverse and the y-coordinate remains the same.
Thus, x cordinate will be -4 and y coordinate will be 1.
Therefore, point S will be (-4,1).
Question 8.
(-2, 3)
Answer:
Given that the points A and B are reflections of each other about the y-axis.
Given that B is reflection of point A in the x-axis and point A is (2,-3).
If a point is reflected across the y-axis, The x-coordinate is taken to be the additive inverse and the y-coordinate remains the same.
Thus, x cordinate will be 2 and y coordinate will be -3.
Therefore, point S will be (2,-3).
Question 9.
(2, -2)
Answer:
Given that the points A and B are reflections of each other about the y-axis.
Given that B is reflection of point A in the x-axis and point A is (2,-2).
If a point is reflected across the y-axis, The x-coordinate is taken to be the additive inverse and the y-coordinate remains the same.
Thus, x cordinate will be -2 and y coordinate will be -2.
Therefore, point S will be (-2,-2).
Question 10.
(-1, -3)
Answer:
Given that the points A and B are reflections of each other about the y-axis.
Given that B is reflection of point A in the x-axis and point A is (-1,-3).
If a point is reflected across the y-axis, The x-coordinate is taken to be the additive inverse and the y-coordinate remains the same.
Thus, x cordinate will be 1 and y coordinate will be -3.
Therefore, point S will be (1,-3).
Use graph paper. For each exercise, plot the given points on a coordinate plane. Then join the points in order with line segments to form a closed figure. Name each figure formed.
Question 11.
H(-5, 1), J(-3, -1), K (-1, 1), and L(-3, 3)
Answer:
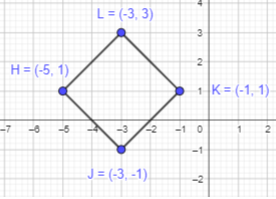
Given points are H(-5, 1), J(-3, -1), K (-1, 1), and L(-3, 3)
To get a closed figure, plot the above points and join them in order.
It is forming a four-sided polygon. All the four sides are equal in length and diagonals are bisecting each other.
Thus, HJKL will form a rhombus as shown in the graph above.
Question 12.
R (2, 1), S (-1, -3), T(4, -3), and U(7, 1)
Answer:
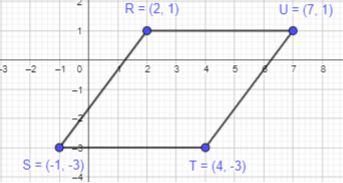
Given points are R (2, 1), S (-1, -3), T(4, -3), and U(7, 1)
To get a closed figure, plot the above points and join them in order.
It is forming a four-sided polygon. The opposite sides are parallel to each other. A parallelogram will have opposite sides in parallel.
Thus, RSTU will form a parallelogram as shown in the graph above.
Question 13.
W (-5, -2), X (-6, -5), Y (-1, -5), and Z (-3, -2)
Answer:
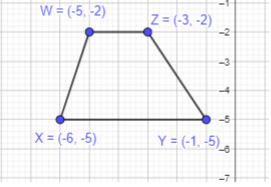
Given points are, W (-5, -2), X (-6, -5), Y (-1, -5), and Z (-3, -2)
To get a closed figure, plot the above points and join them in order.
It is forming a four-sided polygon. All the four sides are of different length, and a pair of opposite sides seems to be parallel which can be a trapezuim.
Thus, WXYZ will form a trapezium as shown in the graph above.
Use graph paper. Plot the points on a coordinate plane and answer each question.
Question 14.
a) Plot points A (-6, 5), C (5, 1), and D (5, 5) on a coordinate plane.
Answer:
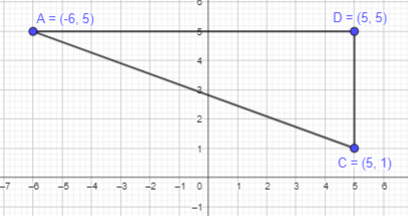
Given points are, A (-6, 5), C (5, 1), and D (5, 5)
To get a closed figure, plot the above points and join them in order.
It is forming a three-sided polygon, which is a triangle. Angle CDA is forming a right angle, so it is a right angle triangle.
Thus, ADC will form a right angle triangle as shown in the graph above.
b) Figure ABCD is a rectangle. Plot point B and give its coordinates.
Answer:
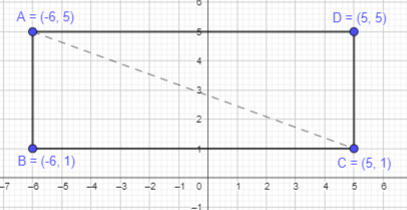
Given points are, A (-6, 5), C (5, 1), and D (5, 5)
A rectangle is combination of two right angle triangle. The base length of given trinagle is 11 units. In a rectangle, opposite sides are equal in length. Therefore, if AD is of 11 units, BC will also be of 11 units and the height will also be same which is 4 units.
Move 11 units towards left from point C and 4 units towards down from point A to mark point B.
Thus, point B will be (-6,1)
Plot point B to form a rectangle.
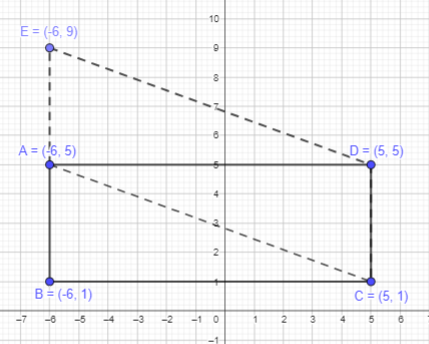
c) Figure ACDE is a parallelogram. Plot point E above \(\overline{\mathrm{AD}}\) and give its coordinates.
Answer:
Given that figure ACDE is a parallelogram. Point E is above \(\overline{\mathrm{AD}}\).
In parallelogram, opposite sides are parallelo to each other. Move 4 units towards upwards from point A nd mark as E.
Join the point EC to form the required parallelogram ACDE.
Thus, Point E will be (-6,9)
Question 15.
a) Plot points A (-3, 2) and B (-3, -2) on a coordinate plane.
Answer:
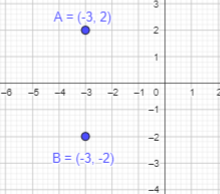
To plot point A(-3,2):
Here, the x-coordinate of A is -3 and the y-coordinate is 2. Start at the Origin. As the x coordinate is negative, move 3 units to the left along the x-axis and 2 units to the top along y -axis.
Thus, the required point A(-3,2) is marked.
To plot point B(-3,-2):
Here, the x-coordinate of A is -3 and the y-coordinate is 2. Start at the Origin. As the x coordinate is negative, move 3 units to the left along the x-axis and 2 units to the down along y -axis as it also is negative.
Thus, the required point A(-3,-2) is marked.
b) Join points A and B with a line segment.
Answer:
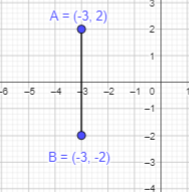
Join A and B points to form a straight line.
c) \(\overline{A B}\) is a side of square ABCD. Name two possible sets of coordinates that could be the coordinates of points C and D.
Answer:
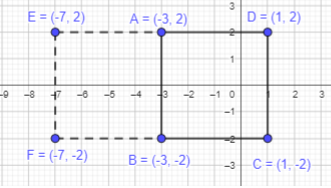
Given that AB is a side of square ABCD. In square all sides are equal. Length of AB is 4 units.
Set 1:
So, first we will start moving towards right from B along with the x-axis and mark the point as C.
Move 4 units towards up from C or towards right from A, mark the point D.
Join ABCD to form a square.
The first possible set of coordinates for C and D will be (1,-2) and (1,2) respectively.
Set 2:
Next, start moving 4 units towards the left from point B and mark it as F.
Move 4 uniits towards up from F or towards left from A, mark the point as E.
Join ABEF to form a square.
The second possible set of coordinates for C and D will be (-7,-2) and (-7,2) respectively.
Question 16.
Plot points A (2, 5) and 8 (2, -3) on a coordinate plane. Figure ABC is a right isosceles triangle. If point C is in Quadrant III, give the coordinates of point C.
Answer:
To plot point A(2,5):
Here, the x-coordinate of A is 2 and the y-coordinate is 5. Start at the Origin. As the x coordinate is positive, move 2 units to the right along the x-axis and 5 units to the top along y -axis.
Thus, the required point A(2,5) is marked.
To plot point B(2,-3):
Here, the x-coordinate of A is 2 and the y-coordinate is -3. Start at the Origin. As the x coordinate is positive, move 2 units to the right along the x-axis and 3 units to the top along y -axis.
Thus, the required point B(2,-3) is marked.
Point C is in Quadrant III and it should form a right angle triangle.
The side AB is of length 8 units, so BC will also remain the same.
Figure ABC is a right isosceles triangle.
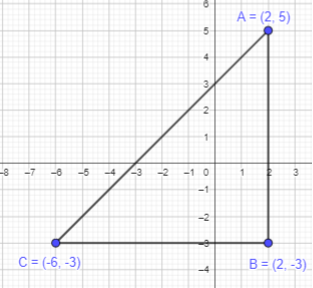
Question 17.
Plot points A (0, 4), B (-4, 0), and C (0, -4) on a coordinate plane.
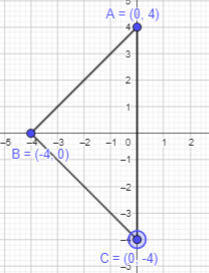
Given points A (0, 4), B (-4, 0), and C (0, -4) are to be plotted on a coordinate plane.
Joining them will form a triangle.
a) What kind of triangle is triangle ABC?
Answer:
Since the point B is at equidistant from A and C.
The lengths of BC and AB will be same.
Thus, ABC will form an isosceles triangle.
b) Figure ABCD is a square. Plot point D on the coordinate plane and give its coordinates.
Answer:
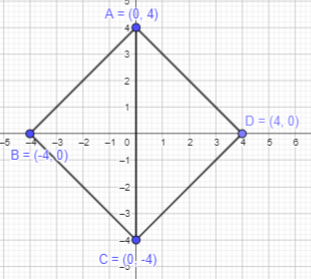
In square, all sides are equal. The length of AB and BC equals 4 units.
D is reflection of point B in the x-axis and point B is (-4,0).
If a point is reflected across the y-axis, The x-coordinate is taken to be the additive inverse and the y-coordinate remains the same.
Therefore, point D will be (4,0)
Thus, the required square ABCD is formed.