Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 9 The Coordinate Plane to score better marks in the exam.
Math in Focus Grade 6 Course 1 B Chapter 9 Answer Key The Coordinate Plane
Math in Focus Grade 6 Chapter 9 Quick Check Answer Key
Use the coordinate plane below.
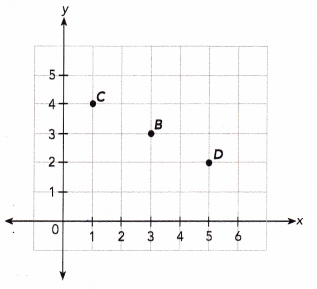
Question 1.
Give the coordinates of points B, C, and D.
Answer:
Point B:
The first coordinate represents distance along x axis which is 3 and the second coordinate represents distance along y axis which is 3.
So, the point P will be (3,3).
Point C:
The first coordinate represents distance along x axis which is 1 and the second coordinate represents distance along y axis which is 4.
So, the point C will be (1,4).
Point D:
The first coordinate represents distance along x axis which is 5 and the second coordinate represents distance along y axis which is 2.
So, the point D will be (5,2).
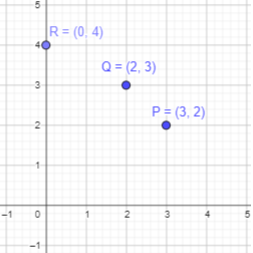
Use graph paper. Plot the points on a coordinate plane.
Question 2.
P (3, 2), Q (2, 3), and R (0, 4)
Answer:
To plot point P (3, 2):
Here, the x-coordinate is 3 and the y-coordinate is 2. Start at the Origin. As the x coordinate is positive, move 3 units along the positive x-axis and 2 units along positive y -axis.
Thus, the required point P (3, 2) is marked.
To plot point Q (2, 3):
Here, the x-coordinate is 2 and the y-coordinate is 3. Start at the Origin. As the x coordinate is positive, move 2 units along the positive x-axis and 3 units along positive y -axis.
Thus, the required point P (2, 3) is marked.
To plot point R (0, 4):
Here, the x-coordinate is 0 and the y-coordinate is 4. As the y coordinate is positive, move 5 units along the positive y-axis and mark it.
Thus, the required point(0, 4) is marked
Identify the number that each indicated point represents.
Question 3.
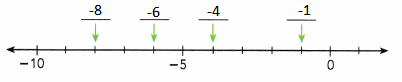
Answer:
To the left of the origin, the x coordinate values will be negative.
Start counting from the origin and note down the values.
The first value will be -1, next will be -4, -6 and -8.
Draw a horizontal number line to represent each set of numbers.
Question 4.
-3, 0, 1, 5, 8
Answer:
-3 is the negative value; therefore mark it to the left of the origin.
0 is the origin. 1,5,8 are the positive values, which are to be marked to the right of the origin.

Question 5.
-15, -11, -9, -7, -2
Answer:
Here, all are negative values. Hence all the values are to be marked to the left of the origin.

Use the symbol || to write the absolute values of the following numbers.
Question 6.
11
Answer:
The distance of an integer from ‘
‘ on the number line irrespective of its direction is called the absolute value of that integer.
Two vertical bars ‘| |’ are used to denote the absolute value.
The absolute value of any positive number is the number itself.
Therefore, the absolute value of 11 will be 11.
Question 7.
-16
Answer:
The absolute value of negative number is the positive of it.
Therefore, the absolute value of -16 or |-16| will be 16.
Question 8.
-21
Answer:
The absolute value of negative number is the positive of it.
Therefore, the absolute value of -21 or |-21| will be 21.
Find the perimeter of each polygon.
Question 9.
Figure ABC is an isosceles triangle.
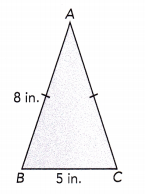
Answer:
Given triangle ABC has two equal sides, thus it will form an isosceles triangle.
The triangle will measure 8 in, 8 in and 5 in.
Perimeter of the triangle will be the sum of all sides, 8+8+5 = 21 in
Question 10.
Figure DEFis an equilateral triangle.
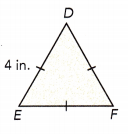
Answer:
Given DEF is an equilateral triangle. Equilateral trinagle will have all equal sides.
All sides of the triangle will measure 4 in.
Perimeter of the triangle will be the sum of all sides, 4+4+4 = 12 in
Question 11.
Figure PQRS is a trapezoid.
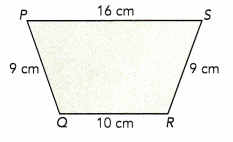
Answer:
Given figure PQRS is a trapezoid. One of the pair of opposite sides are equal in length.
The trapezoid measures 16cm,10cm and 9cm.
Perimeter of the trapezoid will be the sum of all sides, 16+10+9+9 = 44cm
Question 12.
Figure WXYZ is a parallelogram.
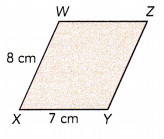
Answer:
Given figure WXYZ is a parallelogram. The opposite sides are equal in length.
The parallelogram measures 8cm and 7cm.
Perimeter of the parallelogram will be the sum of all sides, 8+7+8+7 = 30cm
Question 13.
Figure JKLM is a rhombus.
Answer:
Given figure JKLM is a rhombus. All the sides are equal in length.
Each side will measure 6m in length.
Perimeter of the rhombus will be the sum of all sides, 6+6+6+6 = 24cm