This handy Math in Focus Grade 6 Workbook Answer Key Chapter 12 Review Test detailed solutions for the textbook questions.
Math in Focus Grade 6 Course 1 B Chapter 12 Review Test Answer Key
Concepts and Skills
Match each of the solid figures to its net.
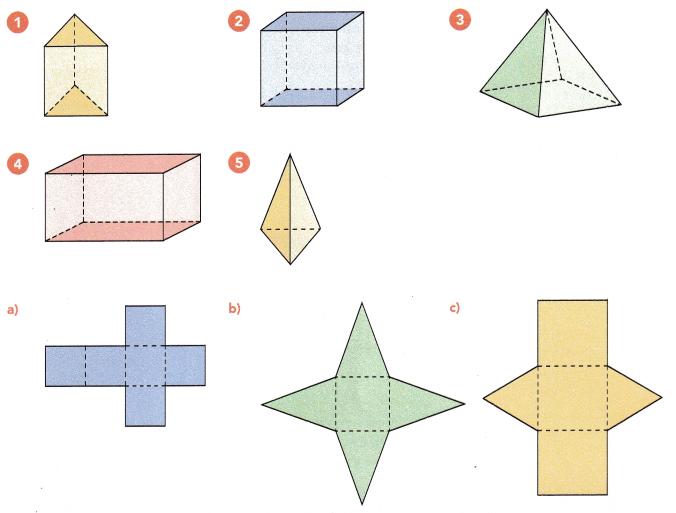
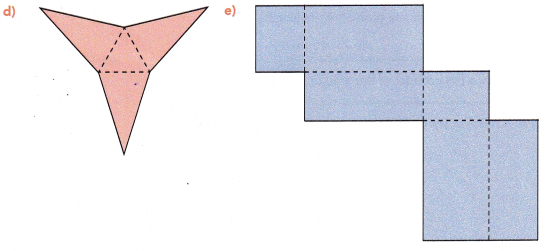
Answer:
The net form of Figure 1 is Figure c.
The net form of Figure 2 is Figure a.
The net form of Figure 3 is Figure b.
The net form of Figure 4 is Figure e.
The net form of Figure 5 is Figure d.
Find the surface area of each solid.
Question 6.
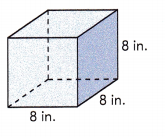
Answer:
Given that the length of the cube is 8 in.
The given figure has 6 faces.
Area of 1 face will be 8×8 = 64 sq.in
Surface area of the given solid = 6×base area
The surface area of the given solid will be 6×64 = 384 sq.in
Question 7.
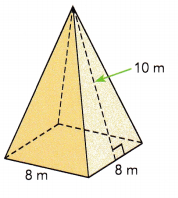
Answer:
Given solid has four triangular faces and one square base.
Area of base will be 8×8 = 64 sq.m
Area of triangle = \(\frac{1}{2}\) × base × width
Area of triangular face will be \(\frac{1}{2}\) × 8 × 10 = 40 sq.m
There are 4 such triangular faces, 4×40 = 160 sq.m
The surface area of the given figure will be 64+160 = 224 sq.m
Find the volume of each prism.
Question 8.
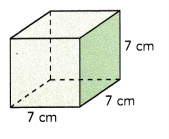
Answer:
Given cube has length of 7 cm.
Area of base = 7×7 = 49 sq.cm
Volume of the prism = base area × height
Volume of the prism will be 49×7 = 343 cu.cm
Question 9.
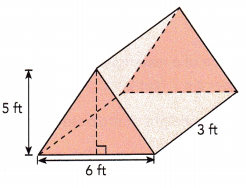
Answer:
Area of triangular base = \(\frac{1}{2}\) ×base×height
Area of the base will be \(\frac{1}{2}\) ×6×5 = 15 sq.ft
Volume of the given prism will be 3×15 = 45 cu.ft
Solve.
Question 10.
The solid below is made up of cubes, each of which has an edge length of 3 inches.
a) What is the volume of one cube?
Answer:
Given that the length of the cube is 3 inches.
Area of one cube will be = 3×3 = 9 sq.in
Volume of the cube= base area × height
Volume of one cube will be = 9×3 = 27 cu.in
b) What is the volume of the solid figure?
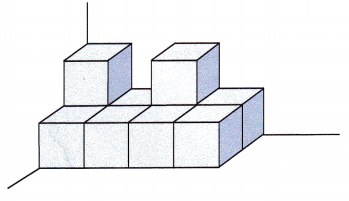
Answer:
The below solid figure has 10 identical cubes.
Therefore, the volume of the solid figure will be 10×27 = 270 cu.in
Problem Solving
Solve.
Question 11.
A fish tank is 50 centimeters long, 30 centimeters wide, and 40 centimeters high. It contains water up to a height of 28 centimeters. How many more cubic centimeters of water are needed to fill the tank to a height of 35 centimeters?
Answer:
Given that a fish tank is 50 centimeters long, 30 centimeters wide, and 40 centimeters high.
Volume of the tank = length × width × height
Volume of water filled up to a height of 28 centimeters is 50×30×28 = 42000 cu.cm
Volume of water to fill up to 35 cm will be 50×30×35 = 52500 cu.cm
More cubic centimeters of water are needed to fill the tank to a height of 35 centimeters will be 52500-42000 = 10500 cu.cm
Question 12.
Find the surface area of a square pyramid given that its base area is 196 square inches and the height of each of its triangular faces is 16 inches.
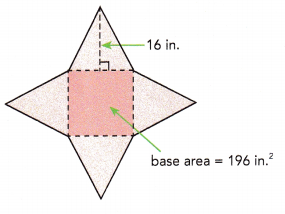
Answer:
Given that the base area of the given square pyramid is 196 sq.in.
Area of square = 196
196 can also be written as 14 × 14
length × length = 196
Length of one side of the square will be 14 cm.
Area of trinagular face will be \(\frac{1}{2}\) × 14 × 16
= 7 × 16
= 112 cu.in
Surface area of the given solid is 4×112 + 196
= 448 + 196
= 644 sq.in
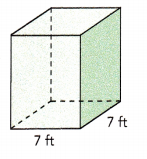
Question 13.
The volume of a rectangular prism is 441 cubic feet. It has a square base with edges that are 7 feet long.
a) Find the height of the prism.
Answer:
Given that the volume of a rectangular prism is 441 cubic feet and it has a square base with edges that are 7 feet long.
Volume of the prism = Area of the base × height
Area of the base = 7×7 = 49 sq.ft
441 = 49 × height
height = 441÷49
height = 9 ft.
Therefore, the height of the prism is 9 ft.
b) Find the surface area of the prism.
Answer:
Area of the square base = length×length = 49 sq.ft
Area of the rectangular base = length×width= 7×9 = 63 sq.ft
There are 2 square bases and 4 rectangular faces.
Therefore, the surface area of the prism will be 2×49 + 4×63
= 98 + 252
= 350 sq.ft
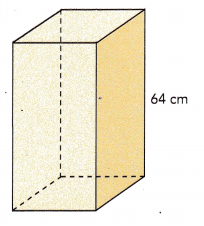
Question 14.
The volume of a rectangular tank with a square base is 63,908 cubic centimeters. Its height is 64 centimeters. Find the length of an edge of one of the square bases. Round your answer to the nearest tenth of a centimeter.
Answer:
Given that the volume of a rectangular tank with a square base is 63,908 cubic centimeters and it is 64 cm high.
Volume of a rectangular prism = Area of base × height
63,908 = Area of base × 64
Area of base will be 63908 ÷ 64 = 998.56 sq.cm
Area of the base when rounded to nearest ten will be 1000.
Area of base = length × length
1000 = length × length
10 × 10 = length × length
Length of an edge of one of the square bases will be 10 cm.