Math in Focus Grade 7 Chapter 8 Review Test Answer Key

This handy Math in Focus Grade 7 Workbook Answer Key Chapter 8 Review Test detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 8 Review Test Answer Key

Concepts and Skills

For this review, r represents radius and h represents height. You may use a calculator and use 3.14 as an approximation for π. Round your answers to the nearest tenth unless otherwise stated.

Question 1.
Find the volume of each cylinder to the nearest unit. Use the given dimensions,
a) r = 4.2 inches; h = 14 inches
Answer:
775 cubic units

Explanation:
The volume of the cylinder is =π r² h
π = 3.14, r = 4.2, h= 14 inches
volume of the cylinder = 3.14×4.2×4.2×14 = 775 cubic units

b) r = 7 centimeters; h = 12 centimeters
Answer:
1846 cubic units

Explanation:|
The volume of the cylinder is =π r² h
π = 3.14, r = 7, h= 12 centimeters
volume of the cylinder = 3.14×7×7×12 = 1846 cubic units

Question 2.
Find the volume of each cone to the nearest unit. Use the given dimensions.
a) r = 3 centimeters; h = 8 centimeters
Answer:
75 cm³.

Explanation:
The volume of each cone is 1/3hπr²
r = 3 centimeters; h = 8 centimeters
Therefore the volume of each cone is = 1/3×8×3.14×3×3 = 75 cm³.

b) r = 8 inches; h = 15 inches
Answer:
1004 cm³.

Explanation:
The volume of each cone is 1/3hπr².
Given r = 8 inches; h = 15 inches and π=3.14
Therefore the volume of each cone is = 1/3×8×3.14×15 ×15 = 1004 cm³.

Question 3.
Find the volume of each pyramid. Use the given dimensions.

a) A square base with an edge length of 6 centimeters; h = 4 centimeters.
Answer:
We are given the cone:
l = 6
h = 4
Use the formula for the volume of a pyramid:
V = \(\frac{1}{3}\)Bh = \(\frac{1}{3}\)l²h
Substitute for l, h:
= \(\frac{1}{3}\) · 6² · 4
Multiply:
= 48 cm³

b) A rectangular base with length of 6 inches and width = 3.3 inches; h = 7 inches.
Answer:
We are given the cone:
l = 6
w = 3.3
h = 7
Use the formula for the volume of a pyramid:
V = \(\frac{1}{3}\)Bh = \(\frac{1}{3}\)lwh
Substitute for l, w, h:
= \(\frac{1}{3}\) · 6 · 3.3 · 7
Multiply:
= 46.2 in³

Question 4.
Find the volume of each sphere to the nearest unit. Use the given dimensions,
a) r = 9.6 centimeters
Answer:
3705 cm³

Explanation:
The volume of each sphere is = 4/3 πr³
Given r = 9.6 centimeters
Volume of the sphere is = 4/3×3.14×9.6×9.6×9.6 = 3705 cm³.

b) d = 26 centimeters
Answer:
9202 cm³.

Explanation:
The volume of each sphere is = 4/3 πr³
Given diameter is = 13 cm
Here we need a radius to calculate the volume of the sphere hence r = d/2 = 26/2 = 13 cm
Volume of the sphere is = 4/3×3.14×13×13×13=9202 cm³.

Question 5.
Find the exact surface area of each solid.

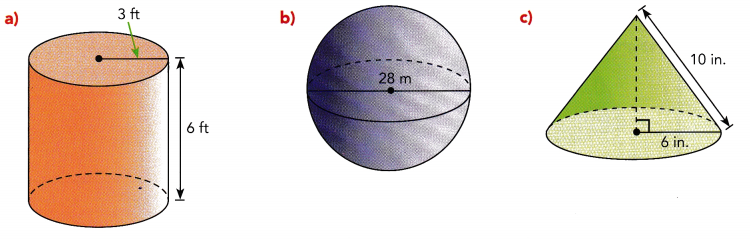
Answer:
a) We are given the cylinder:
r = 3
h = 6
Use the formula for the surface area of a cylinder.
S = 2πr² + 2πrh
Substitute for r, h:
= 2π · 3² + 2π · 3 · 6
Multiply:
= 18π + 36π
Add:
= 54π ft²

b) We are given the sphere:
d = 28
Determine the radius of the sphere:
r = \(\frac{d}{2}\) = \(\frac{28}{2}\) = 14
Use the formula for the surface area of a sphere:
S = 4πr²
Substitute for r:
= 4π · 14²
Multiply:
= 784π m²

c) We are given the cone:
r = 6
l = 10
Use the formula for the surface area of a cone:
S = πr² + πrl
Substitute for r, l:
= π · 6² + π · 6 · 10
Multiply:
= 36π + 60π
Add:
= 96π in²

Question 6.
Find the volume and surface area of each solid. Round to the nearest tenth.
a) A solid cone with a diameter of 5 feet, a slant height of 7 feet, and a height of 6.5 feet.
Answer:
We are given the cone.
d = 5
l = 7
h = 6.5
Find the radius:
r = \(\frac{d}{2}\) = \(\frac{5}{2}\) = 2.5
Use the formula for the volume of the cone:
V = \(\frac{1}{3}\) πr²h
≈ \(\frac{1}{3}\) · 3.14 · 2.5² · 6.5
≈ 42.5 ft³
Use the formula for the surface area of the cone:
S = πr² + πrl
= π · 2.5² + π · 2.5 · 7
= 6.25π + 17.5π
= 23.75π
≈ 23.75 · 3.14
≈ 74.6 ft²

b) A sphere with a radius of 28 millimeters.
Answer:
We are given the sphere:
r = 28
Use the formula for the volume of the sphere:
V = \(\frac{4}{3}\) πr³ = \(\frac{4}{3}\) · 3.14 · 28³
≈ 91,905.7 mm³
Use the formula for the surface area of the sphere:
S = 4πr² ≈ 4 · 3.14 · 28²
≈ 9,487 mm²

c) A solid cylinder with a radius of 1.4 inches and a height of 4.2 inches.
Answer:
We are given the cylinder:
r = 1.4
h = 4.2
Use the formula for the volume of the cylinder:
V = πr²h ≈ 3.14 · 1.4² · 4.2
≈ 25.8 in³
Use the formula for the surface area of the cylinder:
S = 2πr² + 2πrh
= 2π · 1.4² + 2π · 1.4 · 4.2
= 3.92π + 11.76π
= 15.68π
≈ 15.68 · 3.14
≈ 49.2 in²

Problem Solving

Solve. Show your work.

Question 7.
The volume of a cone is 450 cubic centimeters and the radius of the base is 5 centimeters. What is the height of the cone to the nearest tenth?
Answer:
We are given:
V = 450
r = 5
Use the formula for the volume of the sphere:
V = \(\frac{1}{3}\) · πr² · h
Substitute for V, πn r:
450 = \(\frac{1}{3}\) · 3.14 · 5² · h
Multiply:
450 = \(\frac{78.5}{3}\) · h
Multiply:
450 = \(\frac{78.5}{3}\) · h
Multiply both sides by 3:
3 · 450 = 3 · \(\frac{78.5}{3}\) · h
Multiply:
1,350 = 78.5h
Divide both sides by 78.5
\(\frac{1,350}{78.5}\) = \(\frac{78.5h}{78.5}\)
Simplify
h ≈ 17.2 cm

Question 8.
The surface area of a sphere is 498.96 square centimeters. What is the radius of the sphere to the nearest tenth?
Answer:
We are given the sphere:
S = 498.96
Use the formula for the surface area of a sphere:
S = 4πr²
Substitute S and π:
498.96 = 4 · 3.14 · r²
Multiply:
498.96 = 12.56 · r²
Divide each side by 12.56
\(\frac{498.96}{12.56}=\frac{12.56 r^{2}}{12.56}{78.5}\)
Evaluate:
39.7261 ≈ r²
Find the square root of each side:
\(\sqrt[2]{39.7261}\) ≈ r²
Round to the nearest tenth:
r ≈ 6.3 cm

Question 9.
A cone with a height of 6 inches and a slant height of 7.5 inches has a lateral surface with an area of approximately 106 square inches.

a) What is the radius? Round to the nearest tenth.
Answer:
We are given:
h = 6
l = 7.5
A = 106
Use the formula for the cone’s lateral surface area:
A = πrl
Substitute A, l, π to find r:
106 = 3.14 · r · 7.5
Multiply:
106 = 23.55r
Divide both sides by 23.55
\(\frac{106}{23.55}=\frac{23.55 r}{23.55}\)
r ≈ 4.5 in

b) What is the volume of the cone? Round to the nearest tenth.
Answer:
Use the formula for the cone’s volume:
V = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) · 3.14 · 4.5² · 6
≈ 127.2 in³

Question 10.
A cylinder, a cone, and a sphere are shown below. Each solid has a radius of 1 inch and a height of 2 inches. Which of them has the greatest volume? Justify your answer.

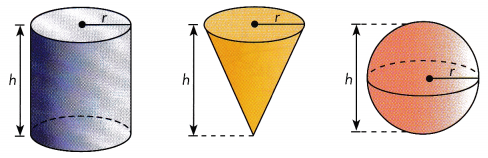
Answer:
We are given:
r = 1
h = 2
Determine the cylinder’s volume:
V_cylinder = πr²h = π · 1² · 2 = 2π
Determine the cone’s volume:
V_cone = \(\frac{1}{3}\) πr²h = \(\frac{1}{3}\) · π · 1² · 2
= \(\frac{2 \pi}{3}\)
Determine the sphere’s volume:
V_sphere = \(\frac{4}{3}\) πr³ = \(\frac{4}{3}\) · π · 1³
= \(\frac{4 \pi}{3}\)
We have:
\(\frac{2 \pi}{3}\) < \(\frac{4 \pi}{3}\) < 2π
V_cone < V_sphere < V_cylinder
The greatest volume is the cylinder’s

Question 11.
Two metal cubes each have an edge length of 4 centimeters. They are melted and recast into a square pyramid with a height of 5 centimeters. Find the area of the base of the pyramid.
Answer:
Determine the volume of the two cubes:
V = 2 · 4³ = 2 · 64 = 128 cm³
Use the formula of a pyramids volume:
V = \(\frac{1}{3}\) Bh
Substitute for V, h:
128 = \(\frac{1}{3}\) · B · 5
Multiply both sides by 3:
3 · 128 = 3 · \(\frac{5B}{3}\)
384 = 5B
Divide by 5:
\(\frac{384}{5}\) = \(\frac{5B}{5}\)
B = 76.8 cm²

Question 12.
A conical party hat has a diameter of 7 centimeters and a slant height of 14.5 centimeters. Paul wants to wrap the lateral surface of the party hat with plastic wrap. How much plastic wrap will he use? Round to the nearest square centimeter.
Answer:
We are given the cone:
d = 7
l = 14.5
Determine the radius of the cone:
r = \(\frac{d}{2}\) = \(\frac{7}{2}\) = 3.5
Determine the lateral surface of the cone:
A = πrl ≈ 3.14 · 3.5 · 14.5 ≈ 159 cm²
= 159 cm²

Question 13.
The composite solid shown is made up of a hemisphere attached to the top of a cube. The diameter of the hemisphere is the same as the edge length of the cube. Find the volume of the composite solid. Round to the nearest tenth.
Answer:

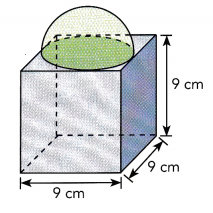
Determine the radius of the hemisphere:
r = \(\frac{9}{2}\) = 4.5
Determine the volume of the hemisphere:
V_hemisphere = \(\frac{1}{2}\) · \(\frac{4}{3}\) πr³
≈ \(\frac{2}{3}\) · 3.14 · 4.5³
≈ 190.8 cm³
Determine the volume of the cube:
V_cube = 9³ = 729 cm³
Determine the volume of the composite solid:
V_solid = V_hemisphere + V_cube
= 190.8 + 729
= 919.8 cm³

Question 14.
The circumference of a fully inflated beach ball is 12π, or about 37.68 inches. What is the radius of the beach ball? What is the volume of
the beach ball? Round to the nearest tenth if necessary.
Answer:
The radius of the beach ball is 6 inches.
The volume of the beach ball is 151 inches.

Explanation:
The circumference of a fully inflated beach ball is 12π.
Circumference of a circle = 2πr
12π=2πr
r=6
Hence radius of the beach ball is 6 inches.
Now we need to calculate the volume of a beach ball
The volume of the sphere is 4/3 πr³
Volume = 4/3×3.14×6×6×6
The volume of the beach ball = 904 inches.

Question 15.
A pyramid made of clay has a square base of length 8 inches and a height of 12 inches. The pyramid is reshaped into a cylinder with a radius of 8 inches. What is the height of the cylinder? Round to the nearest inch
Answer:
The height of the cylinder is 1.27 inches

Explanation:
Given: The base(b) of the square pyramid as 8 inches length and height(h) of the square pyramid as 12 inches.
Now we need to calculate Volume of square pyramid to know the height of cylinder.
The volume of the square pyramid is given by = 1/3(b)²h
Volume = 1/3 (8×8)²×12
Volume = 1/3 (64)×12
Volume = 256 inches
Now pyramid is reshaped into a cylinder with a radius = 8 inches
Volume of cylinder is π r² h
Volume = 3.14×8×8×h
Volume is 256 inches
256 = 3.14×8×8×h
h = 1.27 inches