Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 4 Lesson 4.4 Solving Algebraic Inequalities to score better marks in the exam.
Math in Focus Grade 7 Course 2 A Chapter 4 Lesson 4.4 Answer Key Solving Algebraic Inequalities
Math in Focus Grade 7 Chapter 4 Lesson 4.4 Guided Practice Answer Key
Copy and complete. Solve each inequality and graph the solution set on a number line.
Question 1.
0.2x + 3 + 0.8x ≤ 4
0.2x + 3 + 0.8x ≤ 4
+ 3 ≤ 4 Add the like terms.
+ 3 ≤ 4 – Subtract from both sides.
≤ Simplify.
Answer:
x ≤ 1
Explanation:
Given, 0.2x + 3 + 0.8x ≤ 4
x + 3 ≤ 4
Subtract 3 on both sides.
x + 3 – 3 ≤ 4 – 3
x ≤ 1
Question 2.
\(\frac{1}{4}\)x – 1 + \(\frac{3}{4}\)x > 0
\(\frac{1}{4}\)x – 1 + \(\frac{3}{4}\)x > 0
– 1 > 0 Add the like terms.
– 1 + > 0 + Add to both sides.
> Simplify.
Answer:
x > 1
Explanation:
Given, (1/4)x – 1 + (3/4)x >0
x – 1 > 0
Add 1 on both sides.
x – 1 + 1 > 0 + 1
x > 1
Solve each inequality and graph the solution set on a number line.
Question 3.
2x + 3 < 13 + x
Answer:
x < 10
Explanation:
Given, 2x + 3 < 13 + x
Subtract x and 3 on both sides.
2x + 3 – x – 3 < 13 + x – x – 3
x < 10
Question 4.
1.5x – 3 ≥ 4 + 0.5x
Answer:
x ≥ 7
Explanation:
Given, 1.5x – 3 ≥ 4 + 0.5x
Subtract 0.5x o both sides.
1.5x – 3 – 0.5x ≥ 4 + 0.5x – 0.5x
1x – 3 ≥ 4
Add 3 on both sides.
x – 3 + 3 ≥ 4 + 3
x ≥ 7
Question 5.
4 + \(\frac{1}{3}\)x > 8 + \(\frac{4}{3}\)x
Answer:
x < 4
Explanation:
Given, 4 + (1/3)x > 8 + (4/3)x
Subtract (1/3)x on both sides.
4 + (1/3)x – (1/3)x > 8 + (4/3)x – (1/3)x
4 > 8 -x
Subtract 8 on both sides.
4 – 8 > 8 -x – 8
-x < -4
x < 4
Hands-On Activity
EXPLORE DIVISION AND MULTIPLICATIVE PROPERTIES OF AN INEQUALITY
Work individually.
Step 1: Use a copy of this table. Complete each 
using the symbols > or <.
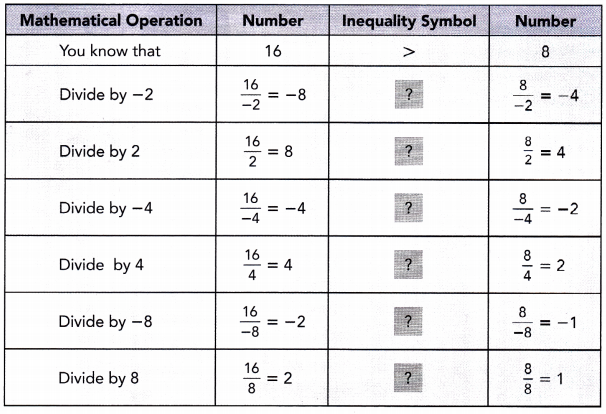
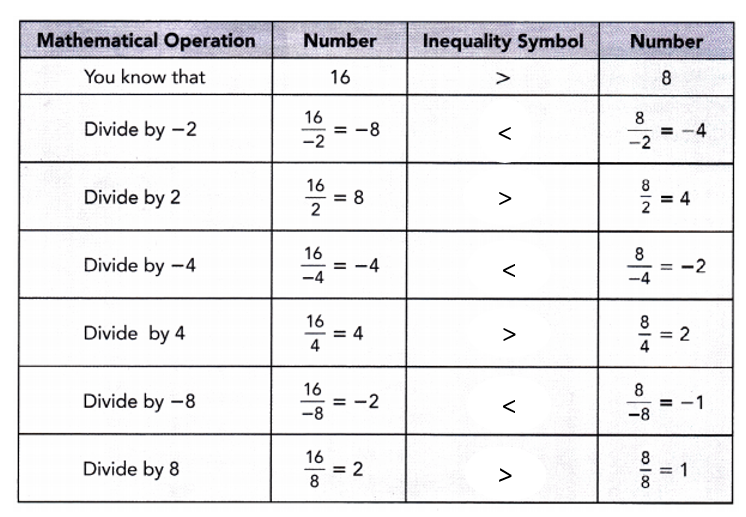
Math Journal What happens to the direction of the inequality symbol when you divide by a positive number? Based on your observation, write a rule for dividing both sides of an inequality by a positive number.
Math Journal What happens to the direction of the inequality symbol when you divide by a negative number? Based on your observation, write a rule for dividing both sides of an inequality by a negative number.
Step 2: Use a copy of this table. Complete each using the symbols > or <.
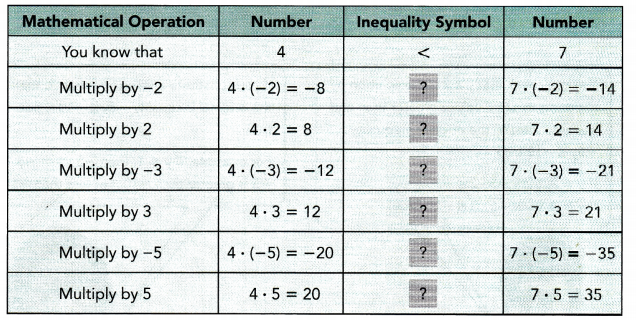
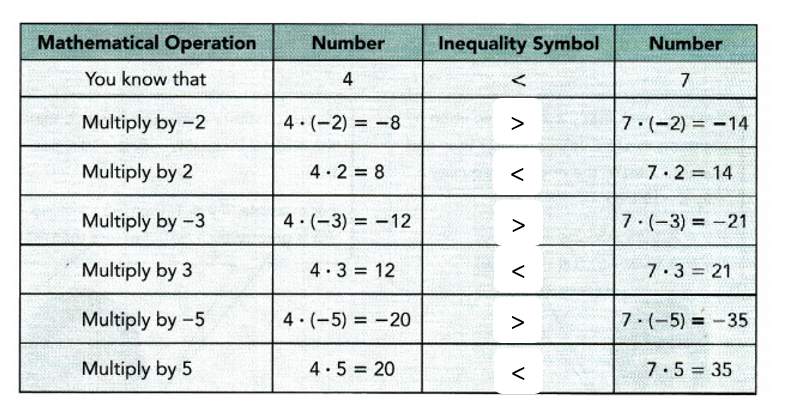
Math Journal What happens to the direction of the inequality symbol when you multiply by a positive number? Based on your observation, write a rule for multiplying both sides of an inequality by a positive number.
Math Journal What happens to the direction of the inequality symbol when you multiply by a negative number? Based on your observation, write a rule for multiplying both sides of an inequality by a negative number.
Solve each inequality and graph the solution set on a number line.
Question 6.
–\(\frac{1}{5}\)w ≤ 2
Answer:
x ≥ -10
Explanation:
Given, -(1/5)x ≤ 2
Multiply 5 on both sides
-(1/5)x × 5 ≤ 2 × 5
-x ≤ 10
x ≥ -10
Question 7.
-7m > 21
Answer:
m < -3
Explanation:
Given, -7m > 21
Divide 7 on both sides.
-7m ÷ 7 > 21 ÷ 7
-m > 3
m < -3
Question 8.
6 > -0.3y
Answer:
y > -20
Explanation:
Given, 6 > -0.3y
Divide 0.3 on both sides.
6 ÷ 0.3 > -0.3y ÷ 0.3
20 > -y
y > -20
Solve each inequality and graph the solution set on a number line.
Question 9.
4y + 7 < 27
4y + 7 < 27
4y + 7 – < 27 – Subtract from both sides.
4y < Simplify.
4y ÷ < ÷ Divide both sides by .
y < Simplify.
Answer:
y < 5
Explanation:
Given, 4y + 7 < 27
Subtract 7 on both sides.
4y + 7 – 7 < 27 – 7
4y < 20
Divide 4 on both sides
4y ÷ 4 < 20 ÷ 4
y < 5
Question 10.
-5y – 9 > 21
-5y – 9 > 21
-5y – 9 + ≥ 21 + Add to both sides.
-5y ≥ Simplify.
– 5y ÷ ≤ ÷ Divide both sides by and reverse the inequality symbol.
y ≤ Simplify.
Answer:
y ≤ -6
Explanation:
Given, -5y – 9 > 21
Add 9 on both sides.
-5y – 9 + 9 > 21 + 9
– 5y > 30
Divide 5 on both sides.
– 5y ÷ 5 > 30 ÷ 5
-y < 6
y ≤-6
Question 11.
\(\frac{1}{2}\)x + \(\frac{3}{4}\) ≥ 5
Answer:
x ≥ (17/2)
Explanation:
Given, (1/2)x + (3/4) ≥ 5
Subtract (3/4) on both sides.
(1/2)x + (3/4) – (3/4) ≥ 5 – (3/4)
(1/2)x ≥ (20 – 3)/4
(1/2)x ≥ (17/4)
Multiply 2 on both sides
(1/2)x × 2 ≥ (17/4) × 2
x ≥ (17/2)
Question 12.
1.5 – 0.3y > 3.6
Answer:
y < -7
Explanation:
Given, 1.5 – 0.3y > 3.6
Subtract 1.5 on both sides.
1.5 – 0.3y – 1.5 > 3.6 – 1.5
-0.3y > 2.1
Divide -0.3 on both sides
-0.3y ÷ (-0.3) > 2.1 ÷ (-0.3)
y < -7
Question 13.
-8y + 32 ≤ -17 – y
Answer:
y ≥ 7
Explanation:
Given, -8y + 32 ≤ -17 – y
Add y on both sides
-8y + 32 + y ≤ -17 – y + y
-7y +32 ≤ -17
Subtract 32 on both sides.
-7y +32 – 32 ≤ -17 -32
-7y ≤ -49
Divide -7 on both sides.
-7y ÷ (-7) ≤ -49 ÷ (-7)
y ≥ 7
Question 14.
4(2 – y) ≥ 20
Answer:
y ≤ -3
Explanation:
Given, 4(2 – y) ≥ 20
8 – 4y ≥ 20
Subtract 8 on both sides
8 – 4y – 8 ≥ 20 – 8
-4y ≥ 12
Divide -4 on both sides
-4y ÷ (-4) ≥ 12 ÷ (-4)
y ≤ -3
Math in Focus Course 2A Practice 4.4 Answer Key
Solve each inequality using addition and subtraction. Then graph each solution set on a number line.
Question 1.
x + 8 > 14
Answer:
x > 6
Explanation:
Given, x + 8 > 14
Subtract 8 on both sides.
x + 8 – 8 > 14 – 8
x > 6
Question 2.
2 ≥ x – 12
Answer:
x ≤14
Explanation:
Given, 2 ≥ x – 12
Add 12 on both sides.
2 + 12 ≥ x – 12 + 12
14 ≥ x
x ≤14
Question 3.
-7x + 5 + 8x > 3
Answer:
x > -2
Explanation:
Given, -7x + 5 + 8x > 3
x + 5 > 3
Subtract 5 on both sides.
x + 5 – 5 > 3 – 5
x > -2
Question 4.
– 2x – 3 + 3x ≥ 12
Answer:
x ≥ 15
Explanation:
Given, -2x – 3 + 3x ≥ 12
x – 3 ≥ 12
Add 3 on both sides.
x – 3 + 3 ≥ 12 + 3
x ≥ 15
Question 5.
29 < \(\frac{2}{3}\)x + 14 + \(\frac{1}{3}\)x
Answer:
x>15
Explanation:
29 < (2/3)x + 14 + (1/3)x
Subtract 14 on both sides.
29 – 14 < (2/3)x + 14 + (1/3)x – 14
15 < x
x>15
Question 6.
\(\frac{1}{5}\)x + 9 + \(\frac{4}{5}\)x > -11
Answer:
x > -20
Explanation:
Given, (1/5)x + 9 + (4/5)x > -11
Subtract 9 on both sides.
(1/5)x + 9 + (4/5)x – 9 > -11 – 9
x > -20
Question 7.
0.7x + 4 + 0.3x ≤ 10
Answer:
x ≤ 6
Explanation:
Given, 0.7x + 4 + 0.3x ≤ 10
Subtract 4 on both sides.
0.7x + 4 + 0.3x – 4 ≤ 10 – 4
x ≤ 6
Question 8.
0.4x – 6 + 0.6x ≥ 19
Answer:
x ≥ 25
Explanation:
Given , 0.4x – 6 + 0.6x ≥ 19
x – 6 ≥ 19
Add 6 on both sides.
x – 6 + 6 ≥ 19 + 6
x ≥ 25
Question 9.
3x + 4 < 2x + 9
Answer:
x < 5
Explanation:
Given, 3x + 4 < 2x + 9
Subtract 4 on both sides.
3x + 4 – 4 < 2x + 9 – 4
3x < 2x + 5
Subtract 2x on both sides
3x – 2x < 2x + 5 – 2x
x < 5
Question 10.
8 – 4x > 12 – 3x
Answer:
x < -4
Explanation:
Given, 8 – 4x > 12 – 3x
Add 3x on both sides
8 – 4x + 3x > 12 – 3x +3x
8 -x > 12
Subtract 8 on both sides.
8 -x – 8 > 12 – 8
-x > 4
x < -4
Question 11.
\(\frac{2}{3}\)x + 2 ≥ 9 – \(\frac{1}{3}\)x
Answer:
x ≥ 7
Explanation:
Given, (2/3)x + 2 ≥ 9 – (1/3)x
Add (1/3)x on both sides
(2/3)x + 2 + (1/3)x ≥ 9 – (1/3)x + (1/3)x
x +2 ≥ 9
Subtract 2 on both sides.
x +2 – 2 ≥ 9 – 2
x ≥ 7
Question 12.
13 + 1\(\frac{3}{5}\)x ≥ 18 + \(\frac{3}{5}\)x
Answer:
x ≥ 5
Explanation:
Given, 13 + 1(3/5)x ≥ 18 + (3/5)x
13 + (8/5)x ≥ 18 + (3/5)x
Subtract (3/5)x on both sides.
13 + (8/5)x – (3/5)x ≥ 18 + (3/5)x – (3/5)x
13 + x ≥ 18
Subtract 13 on both sides.
13 + x – 13 ≥ 18 – 13
x ≥ 5
Question 13.
1.7x + 5 < 16 + 0.7x
Answer:
x < 11
Explanation:
Given, 1.7x + 5 < 16 + 0.7x
Subtract 0.7x on both sides.
1.7x + 5 – 0.7x < 16 + 0.7x – 0.7x
5 + x < 16
Subtract 5 on both sides.
5 + x – 5 < 16 – 5
x < 11
Question 14.
8.5 – 0.9x > 9.8 – 1.9x
Answer:
x < 1.3
Explanation:
Given, 8.5 – 0.9x > 9.8 – 1.9x
Add 0.9x on both sides.
8.5 – 0.9x + 0.9x > 9.8 – 1.9x + 0.9x
8.5 > 9.8 – x
Subtract 9.8 on both sides.
8.5 – 9.8 > 9.8 – x – 9.8
-1 .3 > – x
x < 1.3
Question 15.
Math Journal Solve the inequality 8 + 2x ≥ 12 and show your work. What value is a solution of 8 + 2x ≥ 12 but is not a solution of 8 + 2x > 12?
Answer:
x ≥ 2, x > 2 Both the solutions are not same.
Explanation:
Given, two equations: 8 + 2x ≥ 12
8 + 2x > 12
Let us solve 1st equation: 8 + 2x ≥ 12
Subtract 8 on both sides.
8 + 2x – 8 ≥ 12 – 8
2x ≥ 4
Divide 2 on both sides
2x ÷ 2 ≥ 4 ÷ 2
x ≥ 2
Let us solve 2nd equation:
8 + 2x > 12
Subtract 8 on both sides.
8 + 2x – 8 > 12 – 8
2x > 4
Divide 2 on both sides
2x ÷ 2 > 4 ÷ 2
x > 2
Question 16.
Math Journal Eric solved the inequality 6y ≤ -18 as shown below:
6y ≤ -18
6y ÷ 6 ≥ -18 ÷ 6
y ≥ -3
Describe and correct the error that Eric made.
Answer:
y ≥ 3
Explanation:
Given, 6y ≤ -18
Divide 6 on both sides.
6y ÷ 6 ≥ -18 ÷ 6
y ≥ 3
Solve each inequality using division and multiplication. Then graph the solution set on a number line.
Question 17.
3 ≥ -3x
Answer:
x ≥ -1
Explanation:
Given, 3 ≥ -3x
Divide 3 on both sides.
3 ÷ 3 ≥ -3x ÷ 3
1 ≥ -x
x ≥ -1
Question 18.
-4x > 12
Answer:
x < -3
Explanation:
Given, -4x > 12
Divide -4 on both sides.
-4x ÷ – 4 > 12 ÷ – 4
x < -3
Question 19.
–\(\frac{x}{5}\) ≤ 2
Answer:
x ≥ -10
Explanation:
Given, -(x/5) ≤ 2
Multiply -5 on both sides.
-(x/5) ≤ 2
-(x/5) × -5 ≤ 2 × -5
x ≥ -10
Question 20.
–\(\frac{2}{3}\)x > 8
Answer:
x < -12
Explanation:
Given, -(2/3)x > 8
Multiply 3 on both sides.
-(2/3)x × 3 > 8 × 3
-2x > 24
Divide -2 on both sides.
-2x ÷ -2 > 24 ÷ -2
x < -12
Question 21.
-0.2x ≥ 6
Answer:
x ≤ -30
Explanation:
Given, -0.2x ≥ 6
Divide -0.2 on both sides.
-0.2x ÷ -0.2 ≥ 6 ÷ -0.2
x ≤ -30
Question 22.
9 > -0.5x
Answer:
x > – 18
Explanation:
Given, 9 > -0.5x
Divide – 0.5 on both sides.
9 ÷ -0.5 > -0.5x ÷ -0.5
-18 >x
x > – 18
Solve each inequality using the four operations. Then graph each solution set on a number line.
Question 23.
7y – 3 > 11
Answer:
y > 2
Explanation:
Given, 7y – 3 > 11
Add 3 on both sides.
7y – 3 + 3 > 11 + 3
7y > 14
Divide 7 on both sides.
7y ÷ 7 > 14 ÷ 7
y > 2
Question 24.
-3a + 5 < -7
Answer:
a > 4
Explanation:
Given, -3a + 5 < -7
Subtract 5 on both sides.
-3a + 5 – 5 < -7 – 5
-3a < -12
Divide -3 on both sides.
-3a ÷ -3 < -12 ÷ -3
a > 4
Question 25.
\(\frac{x}{4}\) + \(\frac{3}{16}\) ≥ 1
Answer:
x ≥ (13/4)
Explanation:
(x/4) + (3/16) ≥ 1
multiply 4 on both sides.
((x/4) + (3/16) ) × 4 ≥ 1 × 4
x + (3/4) ≥ 4
Subtract (3/4) on both sides.
x + (3/4) – (3/4) ≥ 4 – (3/4)
x ≥ (13/4)
Question 26.
\(\frac{3}{5}\)a – \(\frac{4}{5}\) < \(\frac{7}{10}\)
Answer:
a < (5/2)
Explanation:
Given, (3/5)a – (4/5) < (7/10)
Add (4/5) on both sides.
(3/5)a – (4/5) + (4/5) < (7/10) + (4/5)
(3/5)a < ((7+(4 × 2))/10)
(3/5)a < (7+8)/10
(3/5)a < 15/10
Divide 3 on both sides.
(3/5)a ÷ 3 < 15/10 ÷ 3
(a/5) < (5/10)
(a/5) < (1/2)
Multiply 5 on both sides.
(a/5) × 5 < (1/2) × 5
a < (5/2)
Question 27.
7 – 0.3x > 4
Answer:
x < 10
Explanation:
Given, 7 – 0.3x > 4
Subtract 7 on both sides.
7 – 0.3x – 7 > 4 – 7
-0.3x > -3
Divide -0.3 on both sides.
-0.3x ÷ -0.3 > -3 ÷ -0.3
x < 10
Question 28.
2.4y + 5 < 29
Answer:
y < 10
Explanation:
Given, 2.4y + 5 < 29
Subtract 5 on both sides.
2.4y + 5 – 5 < 29 – 5
2.4y < 24
Divide 2.4 on both sidea.
2.4y ÷ 2.4 < 24 ÷ 2.4
y < 10
Question 29.
5x + 3 < 7 + 7x
Answer:
x > -2
Explanation:
Given, 5x + 3 < 7 + 7x
Subtract 3 on both sides.
5x + 3 – 3 < 7 + 7x – 3
5x < 4 + 7x
subtract 5x on both sides.
5x -5x < 4 + 7x – 5x
0 < 4 + 2x
-4 < 2x
2x > -4
Divide 2 on both sides.
2x ÷ 2 > -4 ÷ 2
x > -2
Question 30.
11 – 7x ≤ 20 – 8x
Answer:
x ≤ 9
Explanation:
Given, 11 – 7x ≤ 20 – 8x
Subtract 11 on both sides.
11 – 7x – 11 ≤ 20 – 8x – 11
-7x ≤ 9 – 8x
8x – 7x ≤ 9
x ≤ 9
Question 31.
\(\frac{4}{3}\) – \(\frac{5}{6}\)x ≥ –\(\frac{1}{6}\) – \(\frac{2}{3}\)x
Answer:
x ≤ 7
Explanation:
Given, (4/3) – (5/6)x ≥ -(1/6) – (2/3)x
Add (2/3)x on both sides.
(4/3) – (5/6)x + (2/3)x ≥ -(1/6) – (2/3)x + (2/3)x
(4/3) – ((5x – 4x)/6) ≥ -(1/6)
(4/3) -(x/6) ≥ -(1/6)
Add (1/6) on both sides.
(4/3) -(x/6) + (1/6) ≥ -(1/6) + (1/6)
((6 + 1)/6) – x/6 ≥ 0
(7/6) – x/6 ≥ 0
7 – x ≥ 0
7 ≥ x
x ≤ 7
Question 32.
\(\frac{2}{5}\)x + 4 ≤ \(\frac{7}{10}\)x – 8
Answer:
x ≥ 40
Explanation:
Given, (2/5)x + 4 ≤ (7/10)x – 8
Subtract 4 on both sides.
(2/5)x + 4 – 4 ≤ (7/10)x – 8 – 4
(2/5)x ≤ (7/10)x – 12
12 ≤ (7/10)x – (2/5)x
12 ≤ (7 – 4)x/10
12 ≤ 3x/10
Multiply 10 on both sides.
12 × 10 ≤ 3x/10 × 10
120 ≤ 3x
Divide 3 on both sides.
120 ÷ 3 ≤ 3x ÷ 3
40 ≤ x
x ≥ 40
Question 33.
5.4x + 4.2 – 3.8x > 9
Answer:
x > 3
Explanation:
Given, 5.4x + 4.2 – 3.8x > 9
1.6x + 4.2 > 9
Subtract 4.2 on both sides.
1.6x + 4.2 – 4.2 > 9 – 4.2
1.6x > 4.8
Divide 1.6 on both sides.
1.6x > 4.8
1.6x ÷ 1.6 > 4.8 ÷ 1.6
x > 3
Question 34.
6.6 + 1.3x – 5.2x ≤ 14
Answer:
Explanation:
Given, 6.6 + 1.3x – 5.2x ≤ 14
Subtract 6.6 on both sides.
6.6 + 1.3x – 5.2x – 6.6 ≤ 14 – 6.6
-3.9x ≤ 7.4
Divide -3.9 on both sides.
-3.9x ÷ -3.9 ≤ 7.4 ÷ -3.9
x ≥ -(74/39)
Solve each inequality with parentheses using the four operations.
Question 35.
3(y + 2) ≤ 18
Answer:
y ≤ 4
Explanation:
Given, 3(y + 2) ≤ 18
Divide 3 on the both sides.
3(y + 2) ÷ 3 ≤ 18 ÷ 3
(y + 2) ≤ 6
Subtract 2 on both sides.
y + 2 – 2 ≤ 6 – 2
y ≤ 4
Question 36.
8(y – 1) > 24
Answer:
y > 4
Explanation:
Given, 8(y – 1) > 24
Divide 8 on both sides.
8(y – 1) ÷ 8 > 24 ÷ 8
y – 1 > 3
Add 1 on both sides.
y – 1 + 1 > 3 + 1
y > 4
Question 37.
\(\frac{1}{2}\)(a + 1) ≤ 4
Answer:
a ≤ 7
Explanation:
Given, (1/2) (a + 1) ≤ 4
Multiply 2 on both sides.
(1/2) (a + 1) × 2 ≤ 4 × 2
a +1 ≤ 8
Subtract 1 on both sides.
a +1 -1 ≤ 8 – 1
a ≤ 7
Question 38.
\(\frac{2}{3}\)(3 – a) < 3
Answer:
a > -(3/2)
Explanation:
Given, (2/3)(3 – a) < 3
Divide (2/3) on both sides.
(2/3)(3 – a) ÷ (2/3) < 3 ÷ (2/3)
(3 – a) < (9/2)
Subtract 3 on both sides.
3 – a – 3 < (9/2) – 3
-a < (9-6)/2
a > -(3/2)
Question 39.
1.3(2 – x) > 3.9
Answer:
x < -1
Explanation:
Given, 1.3(2 – x) > 3.9
Divide 1.3 on both sides.
1.3(2 – x) ÷ 1.3 > 3.9 ÷ 1.3
2 – x > 3
Subtract 2 on both sides.
2 – x – 2 > 3 – 2
-x > 1
x < -1
Question 40.
3.6(5x – 1) < 5.4
Answer:
x < (1/2)
Explanation:
Given, 3.6(5x – 1) < 5.4
Divide 3.6 on both sides.
3.6(5x – 1) ÷ 3.6 < 5.4 ÷ 3.6
5x -1 < 1.5
Add 1 on both sides.
5x -1 + 1 < 1.5 + 1
5x < 2.5
Divide 5 on both sides.
5x ÷ 5 < 2.5 ÷ 5
x < (1/2)
Question 41.
4 + 2(1 – 3y) < 36
Answer:
y > -5
Explanation:
Given, 4 + 2(1 – 3y) < 36
Subtract 4 on both sides.
4 + 2(1 – 3y) – 4 < 36 – 4
2(1 – 3y) < 32
Divide 2 on both sides.
2(1 – 3y) ÷ 2 < 32 ÷ 2
1 – 3y < 16
Subtract 1 on both sides.
1 – 3y – 1 < 16 – 1
-3y < 15
Divide -3 on both sides.
-3y ÷ -3 < 15 ÷ -3
y > -5
Question 42.
2(3 – x) > 5x – 1
Answer:
x < 1
Explanation:
Given, 2(3 – x) > 5x – 1
6 – 2x > 5x – 1
Add 1 on both sides.
6 – 2x + 1 > 5x – 1 + 1
7 -2x > 5x
Add 2x on both sides.
7 -2x + 2x > 5x + 2x
7 > 7x
Divide 7 on both sides.
7 ÷ 7 > 7x ÷ 7
1 > x
x < 1
Question 43.
\(\frac{5}{9}\)(x + 1) ≥ \(\frac{2}{3}\)
Answer:
x ≥ (1/5)
Explanation:
Given, (5/9)(x + 1) ≥ (2/3)
Multiply 9 on both sides.
(5/9)(x + 1) × 9 ≥ (2/3) × 9
5 (x + 1) ≥ 2 × 3
5 (x + 1) ≥ 6
Divide 5 on both sides.
5 (x + 1) ÷ 5 ≥ 6 ÷ 5
x + 1 ≥ (6/5)
Subtract 1 on both sides.
x + 1 – 1 ≥ (6/5) – 1
x ≥ (6-5)/5
x ≥ (1/5)
Question 44.
\(\frac{2}{3}\)(1 – 3x) > \(\frac{1}{6}\)
Answer:
x < (1/4)
Explanation:
Given, (2/3) (1 – 3x) > (1/6)
Multiply 3 on both sides.
(2/3) (1 – 3x) × 3 > (1/6) × 3
2 (1 – 3x) > (1/2)
Divide 2 on both sides.
2 (1 – 3x) ÷ 2 > (1/2) ÷ 2
1 – 3x > (1/4)
Subtract 1 on both sides.
1 – 3x – 1 > (1/4) – 1
-3x > -(3/4)
Divide -3 on both sides.
-3x ÷ -3 > -(3/4) ÷ -3
x < (1/4)
Question 45.
1.7 + 0.2(1 – x) ≥ 2.7
Answer:
x ≤ -4
Explanation:
Given, 1.7 + 0.2(1 – x) ≥ 2.7
1.7 + 0.2 -0.2x ≥ 2.7
1.9 – 0.2x ≥ 2.7
Subtract 1.9 on both sides.
1.9 – 0.2x – 1.9 ≥ 2.7 – 1.9
-0.2x ≥ 0.8
Divide -0.2 on both sides.
-0.2x ÷ -0.2 ≥ 0.8 ÷ -0.2
x ≤ -4
Question 46.
2.5(3 – 2x) + 1 ≥ 29
Answer:
x ≤ 4.1
Explanation:
Given, 2.5(3 – 2x) + 1 ≥ 29
7.5 – 5x + 1 ≥ 29
8.5 -5x ≥ 29
Subtract 8.5 on both sides.
8.5 -5x – 8.5 ≥ 29 – 8.5
-5x ≥ 20.5
Divide -5 on both sides.
-5x ÷ -5 ≥ 20.5 ÷ -5
x ≤ 4.1
Question 47.
Math Journal Compare solving the inequality -5(x + 6) < 10 with solving the equation -5(x + 6) = 10. Describe the similarities and differences between solving the inequality and solving the equation. Explain how the solution set of the inequality -5(x + 6) < 10 is different from the solution of the equation -5(x + 6) = 10.
Answer:
The solution of the equation -5(x + 6) < 10 is x > -8, which represents the number x can be any number greater than -8.
The solution of the equation -5(x + 6) = 10 is x = -8, here the number x will be only -8 not any other number.
Explanation:
Given two equations are, -5(x + 6) < 10 and -5(x + 6) = 10
Let us consider -5(x + 6) < 10
Divide -5 on both sides.
-5(x + 6) ÷ -5 < 10 ÷ -5
(x + 6) > -2
Subtract 6 on both sides.
x + 6 – 6 > -2 – 6
x > -8
Let us consider the second equation -5(x + 6) = 10
Divide -5 on both sides.
-5(x + 6) ÷ -5 = 10 ÷ -5
(x + 6) = -2
Subtract 6 on both sides.
x + 6 – 6 = -2 – 6
x = -8
Solve each inequality using the four operations.
Question 48.
10 – 3(4a – 3) < 2(3a – 4) – 9.2
Answer:
a > 2.01
Explanation:
Given, 10 – 3(4a – 3) < 2(3a – 4) – 9.2
10 – 12a + 9 < 6a – 8 – 9.2
19 – 12a < 6a – 17.2
Subtract 6a on both sides.
19 – 12a – 6a < 6a – 17.2 – 6a
19 – 18a < -17.2
Subtract 19 on both sides.
19 – 18a – 19 < -17.2 – 19
-18a <-36.2
Divide -18 on both sides.
-18a ÷ -18 <-36.2 ÷ -18
a > 2.01
Question 49.
7(2a – 3) ≤ 5 – 2(3a – 1)
Answer:
a ≤ (7/5)
Explanation:
Given, 7(2a – 3) ≤ 5 – 2(3a – 1)
14a – 21 ≤ 5 – 6a + 2
14a -21 ≤ 7 – 6a
Subtract 7 on both sides.
14a -21 – 7 ≤ 7 – 6a – 7
14a -28 ≤ -6a
Add 6a on both sides.
14a -28 + 6a ≤ -6a + 6a
20a ≤ 28
Divide 20 on both sides.
20a ÷ 20 ≤ 28 ÷ 20
a ≤ (7/5)