Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 8 Lesson 8.1 Translations to score better marks in the exam.
Math in Focus Grade 7 Course 3 B Chapter 8 Lesson 8.1 Answer Key Translations
Math in Focus Grade 8 Chapter 8 Lesson 8.1 Guided Practice Answer Key
Copy and complete on graph paper.
Question 1.
Abigail jogs from point H (3, 2) in a park to point H’, as described by a translation of 5 units to the left and 3 units up. Mark the position of H’ on the coordinate plane.
Answer:
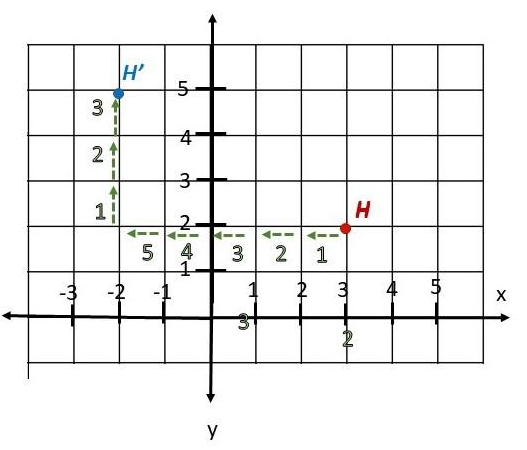
Therefore, H point is on (-2,5)
Copy and complete on graph paper.
Question 2.
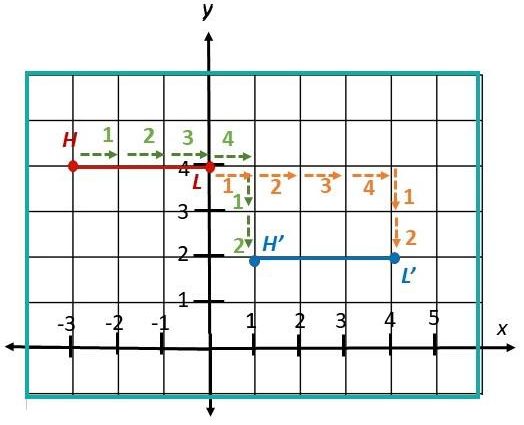
Mr. McBride wanted to set up a barbeque pit in his backyard. He had to move a swing set represented by \(\overline{H L} \text {. }\). He decided to move the swing set by a translation of 4 units to the right and 2 units down to \(\overline{H^{\prime} L^{\prime}}\). Draw and mark \(\overline{H^{\prime} L^{\prime}}\) on the coordinate plane.
Answer:
Technology Activity
Explore The Properties Of Translations With Geometry Software
Step 1.
Draw a line segment using a geometry software program.
Step 2.
Select the Translate function, within the Transform menu. Enter the number of units by which you wish to translate the line segment. Translate the line segment to its new position.
Step 3.
How is the length and position of the new line segment related to the original line segment?
Think Math
A horizontal segment is translated horizontally. Is the image parallel to the original segment? Does a translation always map a segment onto a parallel segment? Explain.
Step 4.
Repeat Step 2 using a triangle and then a rectangle. Observe how each figure is related to its image.
Step 5.
How do the size and shape of the figures change under a translation? Do the parallel sides of the rectangle remain parallel? Do the perpendicular sides of the rectangle remain perpendicular?
Math Journal
Which of these properties does a translation seem to preserve: lengths, shapes, parallel lines, or perpendicular lines? Explain.
Draw Images After Translations.
From the activity, you have observed that translations preserve shape, size, parallelism, and perpendicularity.
When a figure is drawn on a coordinate plane, you can easily draw its image. You need only to find the images of the vertices and connect them appropriately.
Complete on graph paper.
Question 3.
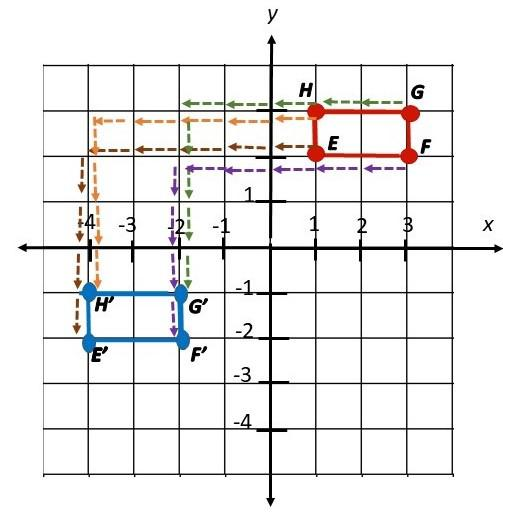
Tim is creating a wrapping paper design on his computer. He wants to move figure EFGH by translating it 5 units to the left and 4 units down. E, F, G, and FI have the coordinates (1, 2), (3, 2), (3, 3), and (1, 3). Draw EFGH and E’F’G’H’ on the same coordinate plane. Use 1 grid square on both axes to represent 1 unit for the interval from —4 to 3. Then complete the following statements.
E (1, 2) is mapped onto E’ (![]() ,
, ![]() ).
).
F(3, 2) is mapped onto F’ (![]() ,
, ![]() ).
).
G (3, 3) is mapped onto G’ (![]() ,
, ![]() ).
).
H (1, 3) is mapped onto H’ (![]() ,
, ![]() ).
).
Answer:
E (1, 2) is mapped onto E’ (-4,-2).
F(3, 2) is mapped onto F’ (-2,-2).
G (3, 3) is mapped onto G’ (-2,-1).
H (1, 3) is mapped onto H’ (-4,-1).
Complete.
Question 4.
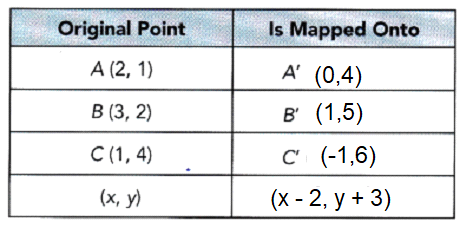
A triangle has coordinates A (2, 1), B (3, 2), and C (1, 4). It is moved under the translation 2 units to the left and 3 units up. Find the coordinates of the image triangle A’B’C’. Then state the new coordinates for any point (x, y) under this translation.

To find the coordinates of A’, B’, and C’, subtract 2 units from the x-coordinate and add 3 units to the y-coordinate of A, B, and C.

Answer:
Math in Focus Course 3B Practice 8.1 Answer Key
Find the coordinates of the image under each translation.
Question 1.
P (0, 2) is translated by 8 units to the left.
Answer: P is mapped onto P’ (-8,2).
Question 2.
Q(-3, 5) is translated by 3 units to the right and 10 units up.
Answer: Q will be (0, 15) of the coordinate plane.
Question 3.
R(-4, -2) is translated by 1 unit to the left and 6 units up.
Answer: R(-4, -2) is mapped onto R'(-5, 4).
Copy each diagram on graph paper and draw the ¡mage under each translation.
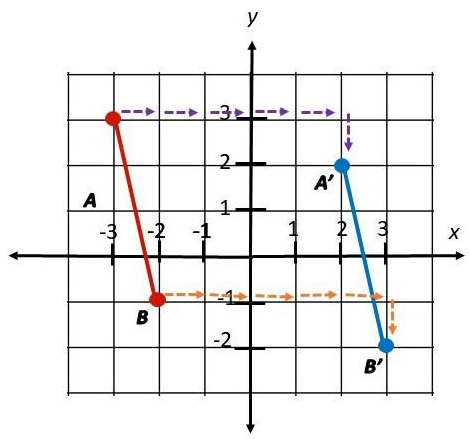
Question 4.
\(\overline{A B}\) is translated 5 units to the right and 1 unit down.
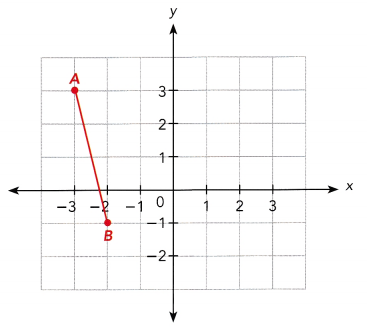
Answer:
Question 5.
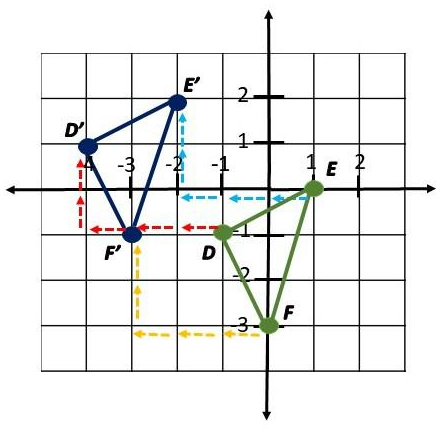
Triangle DEF is translated 3 units to the left and 2 units up.
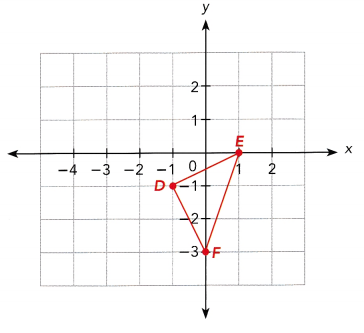
Answer:
Find the coordinates of each point using the given translation. Label the images on a coordinate plane.
Question 6.
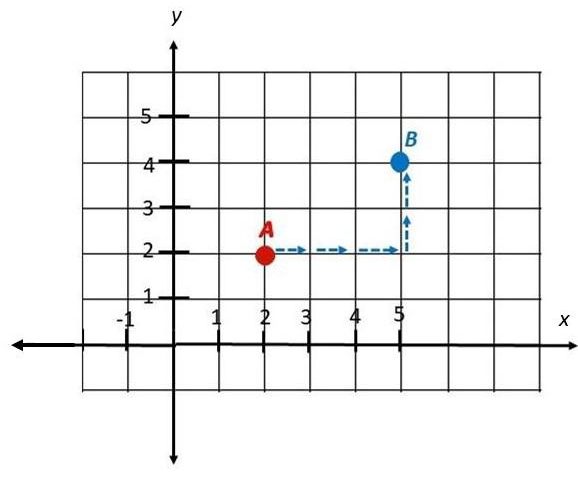
Jon’s apartment is located at A (2, 2). He uses the translations described in a) to d) to visit each of his neighbors.
a) From A (2, 2), translate by 3 units to the right, 2 units up to B.
Answer:
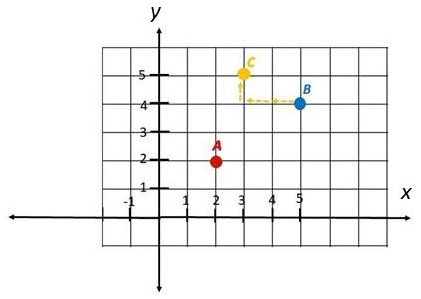
b) From B, translate by 2 units to the left, 1 unit up to C.
Answer:
c) From C, translate by 1 unit to the right, 2 units down to D.
Answer:
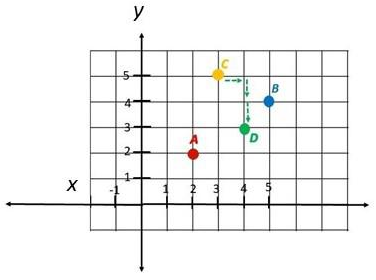
d) From D, translate by 2 units to the left, 3 units down to E.
Answer:
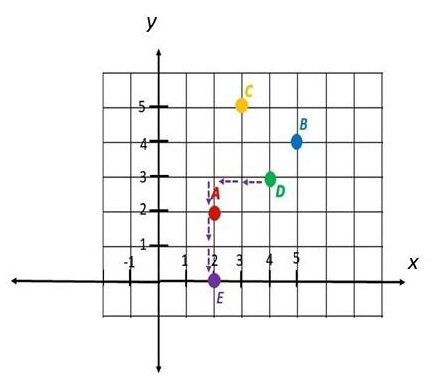
Solve. Show your work.
Question 7.
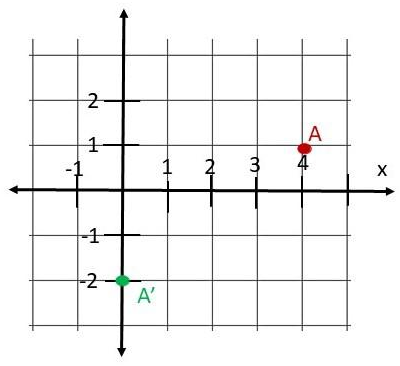
The base of a box is at ABCD. It is moved by a translation to a new position A’B’C’D’. The table shows the position to which A was mapped. Find the new position of the other three vertices of the base. Copy and complete the table.
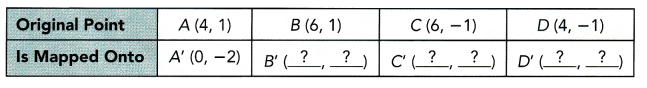
Answer:

Question 8.
A crane moved a cargo pallet from ABCD to other positions on the ship’s deck.
a) Find the coordinates of A’B’C’D’ under a translation that moves each point (p, q) to (p + 4, q + 1). Copy and complete the table. Draw A’B’C’D’ on a graph paper.
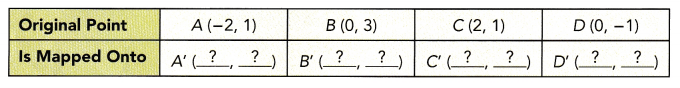
Answer:
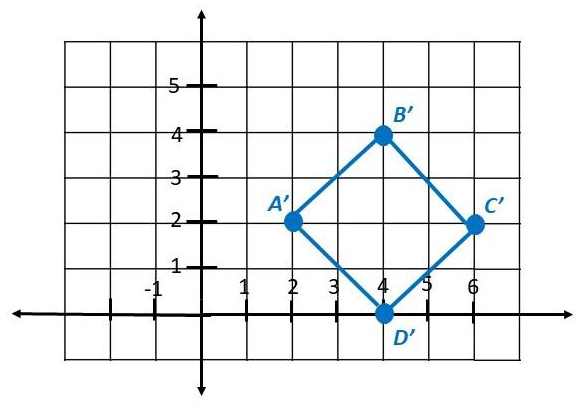
b) The position of A”B”C”D” is shown on the coordinate plane. State the new coordinates of any point (x, y) under the translation from ABCD to A”B”C”D”.
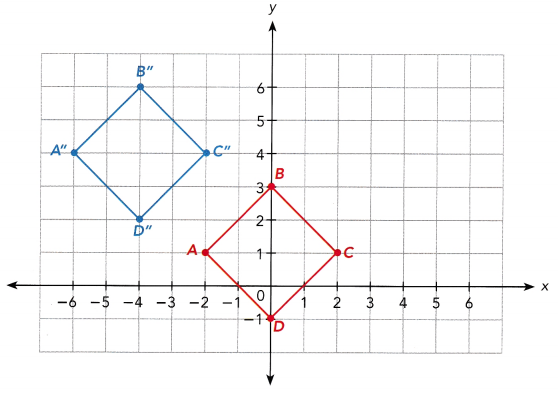
Answer:
A,B,C and D are on (-2, 1), (0, 3), (2, 1) and (0, -1), A” will have coordinates (-6, 4), and B” has (-4, 6). On the other hand, C” will be lying on (-2, 4) and D” is on (-4, 2).
Question 9.
A computer program T instructs a robotic arm to move an object on the coordinate plane 2 units to the right and 3 units down. The object at point P is translated by T to point P’. Find the coordinates of P if point P’ is (3, 3).
Answer: The original point for P'(3, 3) is P(1, 6).
Question 10.
A line has the equation y = x. It is translated up by 3 units. What is the equation of the new line? How do the slopes of the line and its image compare?
Answer:
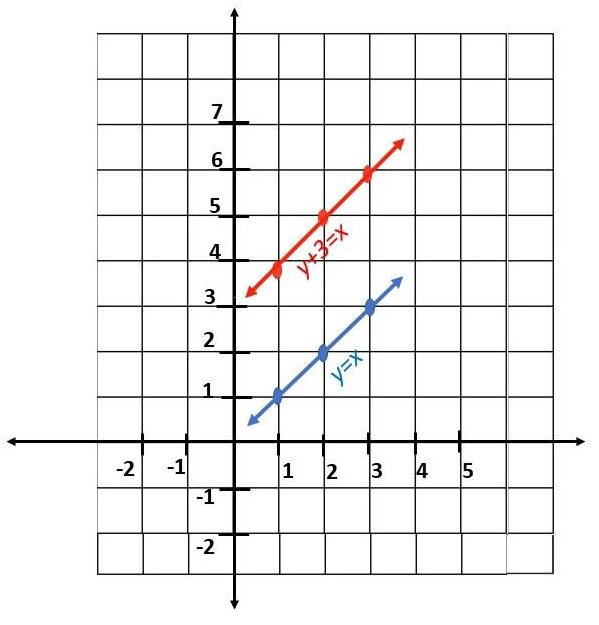
Both the original and new line segment are linear but y + 3 = x is 3 units above y = x.
Question 11.
In a wallpaper pattern, a vertical stripe at x = -1 is copied by moving it to x = 1. Describe the translation of this stripe both verbally and algebraically.
Answer:
First locate at x at -1 on the coordinate plane, then know the position of the point at 1. The distance of the two would determine the number of units it move, so the translation is 2 units. Also the original points is x at -1 and then it moved it to right. Therefore, the translation is 2 units to the right.