Math in Focus Grade 8 Chapter 7 Review Test Answer Key

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 7 Review Test to score better marks in the exam.

Math in Focus Grade 8 Course 3 B Chapter 7 Review Test Answer Key

Concepts and Skills

For this review, you may use a calculator. Use 3.14 as an approximation for π.
Round your answer to the nearest tenth where necessary.

Question 1.
Find the value of x in each of the following diagrams.
a)

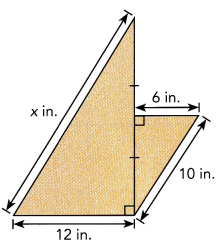
Answer:
The value of x is 17.69 approximately 18 in,

Explanation:
First we find the altitude a for smaller right traiangle,
a² + 6² = 10²,
a² = 100 -36 = 64 so a is square root of 64 is 8 inches as bigger right triangle
altitude is twice the smaller one so it is 2 X 8 =16 inches now
x² = 12² + 16²,
x² = 144 + 169 = 313, therefore x is square root of 17.69 approximately 18 in.

b)

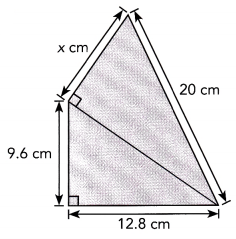
Answer:
The value of x is 12 cm,

Explanation:
Given two right triangles first we calculate hypotenuse be y of
right triangle of width 12.8 cm and height  9.6 cm so
y ² = 9.6² + 12.8² = 92.16 + 163.84 = 256,
so the value of y is square root of 256 is 16 cm,
Now the value of x is  x² + 16² = 20²,
x² = 400 – 256 = 144 , the value of x is square root of 144 is 12 cm.

c)

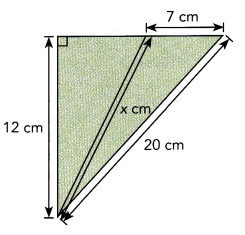
Answer:
The value of x is approximately equal to 19 cm,

Explanation:
Applying pythagorean we have
x² + 7² = 20²,
x² = 400 – 49 = 351, the value of x is square root of 351 is 18.734,
so x is approximately equal to 19 cm.

Question 2.
Find the distance between each pair of points. Which pair of points are the greatest distance apart?
a) A(5, 2), B(8, 5)
Answer:
To find the distance of two points, use the distance formula given by the square root of the sum of the x-coordinate of the second point minus the x-coordinate of the first point and the y-coordinate of the second point minus the y-coordinate of the first point Also. note that there is no negative magnitude(distance) Then, let A(5, 2) be (x₁, y₁) whiLe B(8, 2) be (x₂, y₂) and e be the distance of A to B.
e = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Formula.
= \(\sqrt{(8-5)^{2}+(2-2)^{2}}\)    Substitution.
= \(\sqrt{3^{2}+0^{2}}\)    Subtract.
= \(\sqrt{9+0}\)    Evaluate the squares.
= \(\sqrt{9}\)    Add.
= ±3 Evaluate.
Therefore, A is 3 units away from B.

b) C(-3, 2), D(2, 3)
Answer:
Apply the distance formula then Let C(-3, 2) be (x₁, y₁) while D(2, 3) be (x₂, y₂) and f be the distance of C to D.
e = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Formula.
= \(\sqrt{(2-(-3))^{2}+(3-2)^{2}}\)    Substitution.
= \(\sqrt{5^{2}+1^{2}}\)    Subtract.
= \(\sqrt{25+1}\)    Evaluate the squares.
= \(\sqrt{26}\)    Add.
≈ ±5.1    Evaluate.
Therefore, the distance of C to D is 5.1 units

c) L(1, -3), N(-2, -1)
Answer:
Use the distance formula then let L(1, -3) be (x₁, y₁) white N(-2, -1) be (x₂, y₂) and g be the distance of L to N.
e = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Formula.
= \(\sqrt{((-2)-1)^{2}+((-1)-(-3))^{2}}\)    Substitution.
= \(\sqrt{(-3)^{2}+2^{2}}\)    Subtract.
= \(\sqrt{9+4}\)    Evaluate the squares.
= \(\sqrt{13}\)    Add.
≈ ± 3.6     Evaluate.
Therefore, L is 3.6 units away from N.

d) Y(-3, -3), Z(0, 4)
Answer:
Let Y(-3, -3) be (x₁, y₁) while Z(0, 4) be (x₂, y₂) and h be the distance of Y to Z then apply the distance formula.
e = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Formula.
= \(\sqrt{(0-(-3))^{2}+(4-(-3))^{2}}\)    Substitution.
= \(\sqrt{3^{2}+7^{2}}\)    Subtract.
= \(\sqrt{9+49}\)    Evaluate the squares.
= \(\sqrt{58}\)    Add.
≈ ± 7.6     Evaluate.
Therefore, Y is 7.6 units away from Z.

Since A is 3 units away from B. the distance of C to D is 5.1 units, L is 3.6 units away from N. and Y is 7.6 units away from Z. Therefore, the points with largest distance is Y and Z.

Question 3.
Find the volume of each of the following composite solids.
a)

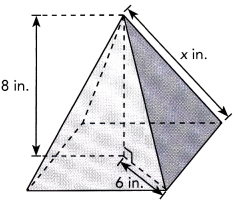
Answer:
The volume of given solid is 120 in³,

Explanation:
First we calculate x,
x² = 6² + 8²,
x² = 36 + 64 = 100, the value of x is square root of 100 is 10 in,
Now the volume of given soild is \(\frac{1}{3}\) • (base edge)² X h =
\(\frac{1}{3}\) • (6)² X 10 in = 120 in³.

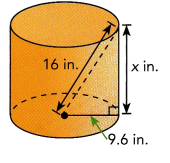
b)

Answer:
The volume is 3704.094 in³,

Explanation:
First we calculate value of  x which is height of cylinder,
Applying pythagorean theorem 16² = 9.6² + x²,
x² = 256 – 92.16 = 163.84, the value of x is square root of
163.84 is 12.8 in now volume of cylinder is πr²h =
3.14 X 9.6 X 9.6 X 12.8 = 3704.094 in³.

c)

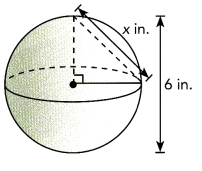
Answer:
The volume is 113.04 in³,

Explanation:
We have height of sphere is 2r, so r = 6/2 = 3 in,
Now volume of sphere is \(\frac{4}{3}\) • πr³ = \(\frac{4}{3}\) X 3.14 X 3 X 3 X 3 = 113.04 in³.

Question 4.
Find the value of x in each of the following diagrams.
a)

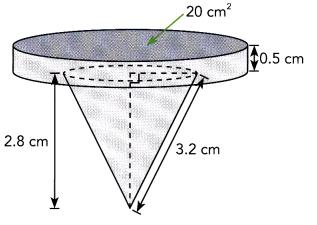
Answer:
To solve for the voLume of the composite soLid, add the volume of the cyLinder to the voLume of the cone. For the volume of the cylinder,
Volume of Cylinder = Area of the base · height of Cylinder
= 20 · 0.5
= 10
Thus, the cylinder has a volume of 10 cubic centimeters. Next, solve for the volume of the cone. First find the radius of its base. Notice that the radius r of the base, the slanted side s and the height j of the cone forms a right triangle with the slanted side as the hypotenuse. Use the Pythagorean Theorem which describes the sum of the square of the legs of a right triangle to be equal to the square of the hypotenuse.
j² + r² = s²      Use the Pythagorean Theorem.
(2.8)² + r² = (3.2)²      Substitution
7.84 + r² = 10.24    Multiply.
7.84 + r² – 7.84 = 10.24 – 7.84     Subtract 7.84 to both sides.
r² = 2.4    Simplify.
r = \(\sqrt{2.4}\)    Find the positive square root.
r ≈ 1.5     Simplify.
Thus, radius r measures around 1.5 cm. Now solving for the volume of the cone, note that the area of a circle (which is the base of the cone) is pi multiplied to the square of the radius and use 3.14 as the value of π.
Volume of Cone = \(\frac{1}{3}\) · Area of the base · Height of Cone
= \(\frac{1}{3}\) πr² · j
= \(\frac{1}{3}\) (3.14) · (1.5)² · 2.8
≈ 6.6
So, the volume of the cone is about 6.6 cubic centimeters. Now for the total volume of the composite solid,
Volume of the Composite Solid = Volume of the Cone + Volume of the Cylinder
= 6.6 + 10
= 16.6
Therefore, the composite solid has a 16.6 cm³ volume.

b)

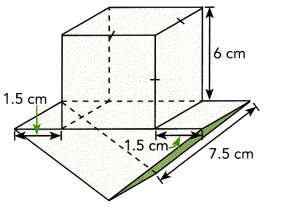
Answer:
To solve for the volume of the composite solid, add the volume of the cube to the volume of the triangular prism. For the volume of the cube,
let s be the measure of the sides.
Volume of Cube = s³  Formula.
= 6³     Substitution.
= 216    Evaluate.
Thus, the volume of the cube is 216 cubic centimeters. Next for the triangular prism, first solve for the measure of its base. Notice that the edges of the triangular prism has a 1.5 centimeters distance from the ends of the side of the cube. Then the length of the side of the triangular base of the prism can be computed.
Measure of the Base = Measure of the Side of the Cube + 1.5 + 1.5
= 6 + 1.5 + 1.5
= 9
So, the side of the base of the triangular prism measures 9cm. Then, find the altitude of the triangular base of the prism. Notice that half of the length of the base side of the prism denoted as e, the slanted side s, and the altitude a creates a right triangle with the slanted side as the hypotenuse. Then, applying Pythagorean Theorem states that the sum of the square of the legs of a right triangle is equal to the square of the hypotenuse,
(\(\frac{e}{2}\))² + a² = s²    Use the Pythagorean Theorem.
(\(\frac{9}{2}\)) + a² = (7.5)²     Substitution.
(4.5)² + a² = (7.5)²    Divide.
20.25 + a² = 56.25    Multiply.
20.25 + a² – 20.25 = 56.25 – 20.25   Subtract 20.25 to both sides.
a² = 36    Evaluate.
a = \(\sqrt{36}\)    Find the positive square root.
a = 6 Simplify.
Thus, the altitude of the triangLe is 6 centimeters Then, note that the area of a triangle (which is the base of this prism) is half of its length multiplied by the aLtitude. Also, notice that the side of the cube is equal to the height of the triangular prism so the height h of the prism is equal to 6 centimeters. Solving for the volume of the triangular prism,
Volume of Triangular Prism = Area of the Base · Height of the Prism
= \(\frac{1}{2}\) · e a · h
= (\(\frac{1}{2}\) · 9 · 6) · 6
= 27 · 6
= 162
Thus, the triangular prism has a volume of 162 cubic centimeters. Now, for the total volume of the composite solid,
Volume of the Composite Solid = Volume of the Cube + Volume of the Triangular Prism
= 216 + 162
= 378
Therefore, tne composite solid has a 378 cm³ volume.

Problem Solving

Solve. Show your work.

An interactive game teaches users how to find the distance between two points on a coordinate plane. Each unit on the grid equals 1 kilometer. Use the grid for questions 5 and 6.

Question 5.
Find the distance between the farmer and each location.
a) River
b) Pond
c) Town
d) Orchard

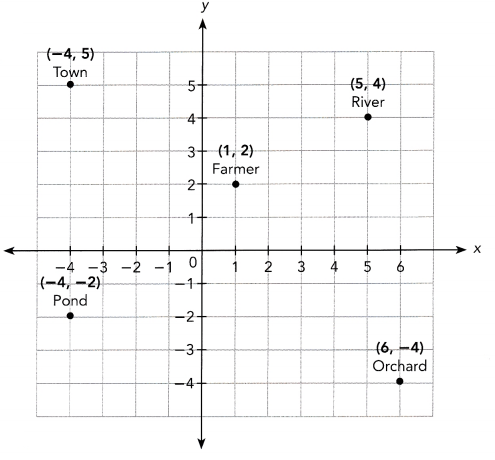
Answer:
a) To find the distance of two points, use the distance formula given by the square root of the sum of the x-coordinate of the second point minus the x-coordinate of the first point and the y-coordinate of the second point minus the y-coordinate of the first point Also, note that there is no negative magnitude(distance). Then, let Mr. Farmer at (1, 2) be (x₁, y₁) white the river at (5,4) be (x₂, y₂) and e be the distance of Mr Farmer and the river.
e = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Formula.
= \(\sqrt{(5-1)^{2}+(4-2)^{2}}\)     Substitution.
= \(\sqrt{4^{2}+2^{2}}\)      Subtract.
= \(\sqrt{16+4}\)     Evaluate the squares.
= \(\sqrt{20}\)     Add.
≈ ± 4.5 Evaluate.
Therefore, Mr. Farmer is approximate[y 4.5 kilometers away from the river.

b. Apply the distance formula again letting Mr. Farmer at (1, 2) be (x₁, y₁) and pond (-4, -2) be (x₂, y₂) and f be the distance of the pond and Mr. Farmer
f = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Formula.
= \(\sqrt{((-4)-1)^{2}+((-2)-2)^{2}}\)     Substitution.
= \(\sqrt{(-5)^{2}+(-4)^{2}}\)      Subtract.
= \(\sqrt{25+16}\)     Evaluate the squares.
= \(\sqrt{41}\)     Add.
≈ ± 6.4   Evaluate.
Therefore, the distance of Mr. Farmer to the pond is about 6.4 kilometers.

c) Use the distance formula then let Mr. Farmer at (1, 2) be (x₁, y₁) while the town at (-4, 5) be (x₂, y₂) and g be the distance of Mr. Framer to the town.
g = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Formula.
= \(\sqrt{((-4)-1)^{2}+(5-2)^{2}}\)     Substitution.
= \(\sqrt{(-5)^{2}+3^{2}}\)      Subtract.
= \(\sqrt{25+9}\)     Evaluate the squares.
= \(\sqrt{34}\)     Add.
≈ ± 5.8     Evaluate.
Therefore, Mr Farmer is around 5.8 kilometers away from the town

d) Let Mr Farmer (1, 2) be (x₁, y₁) while Orchard (6, -4) be (x₂, y₂) and h be the distance of Mr. Farmer and the orchard then apply the distance formula.
h = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Formula.
= \(\sqrt{(6-1)^{2}+((-4)-2)^{2}}\)     Substitution.
= \(\sqrt{5^{2}+(-6)^{2}}\)      Subtract.
= \(\sqrt{25+36}\)     Evaluate the squares.
= \(\sqrt{61}\)     Add.
≈ ± 7.8     Evaluate.
Therefore, Mr Farmer is approximately 7.8 kilometers away from the orchard.

Question 6.
The farmer wants to go fishing in either the river or the pond. Which one is closer to his current position? How many kilometers fewer will he walk if he chooses the source that is closer?
Answer:
The objective is to determine the which body of water is closer to Mr. Farmer at (1, 2) and the difference of the distance of the bodies of water to one another.

First, determine the distance of the farmer to the first body of water which is the river. Apply the distance formula given by the square root of the sum of the x-coordinate of the second point minus the x-coordinate of the first point and the y-coordinate of the second point minus the y-coordinate of the first point. Also, note that there is no negative magnitude(distance). Then, Let Mr. Farmer at (1, 2) be (x₁, y₁) while the river at (5, 4) be (x₂, y₂) and p be the distance of Mr. Farmer and the river
p = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) Formula.
= \(\sqrt{(5-1)^{2}+(4-2)^{2}}\)    Substitution.
= \(\sqrt{4^{2}+2^{2}}\)      Subtract.
= \(\sqrt{16+4}\)      Evaluate the squares.
= \(\sqrt{20}\)    Add.
≈ ± 4.5 Evaluate.
Thus, Mr. Farmer is about 4.5 units away from the river

Next, determine the distance of Mr. Farmer to the pond by using the distance formula again Letting Mr. Farmer at (1, 2) be (x₁, y₁) pond (-4, -2) be (x₂, y₂) and y be the distance of the pond and Mr. Farmer
y = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) Formula.
= \(\sqrt{((-4)-1)^{2}+((-2)-2)^{2}}\)    Substitution.
= \(\sqrt{(-5)^{2}+(-4)^{2}}\)      Subtract.
= \(\sqrt{25+16}\)      Evaluate the squares.
= \(\sqrt{41}\)    Add.
≈ ± 6.4    Evaluate.
Thus, the distance of Mr. Farmer to the pond is around 6.4 units. Since the distance of the river to Mr. Farmer is smaller than the distance of the pond to Mr Farmer, therefore, the river is cLoser to his position.

Lastly, to determine the difference of the distance, subtract the distance of the farmer to the river to the distance of the farmer to pond.
Distance to the Pond – Distance to the River
6.4 – 4.5
1.9
Therefore, the difference of the distance of the pond and river to Mr. Farmer is 1.9 units.

Question 7.
Candy builds a cage for some chickens out of wood and wire mesh, as shown below. The two slanted sides of the cage are the same size and shape. Find the height of the cage.

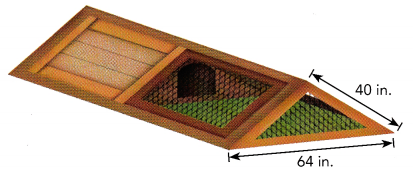
Answer:
The height of the cage is 24 in,

Explanation:
Given Candy builds a cage for some chickens out of wood and
wire mesh, as shown the two slanted sides of the cage are
the same size and shape, we take width as 64/2= 32 in and consider
right triangle and apply pythagorean theorem to find height h of the cage as
h² + 32² = 40²,
h² = 1600 – 1024 = 576, so h is square root of 576 is 24 in.

Question 8.
A straw that is ‘12 centimeters long fits inside a glass. The height of the glass is 7.5 centimeters. Find the radius of the glass.

Answer:
The radius of the glass is 4.68 centimeters,

Explanation:
Given a straw that is ‘12 centimeters long fits inside a glass.
The height of the glass is 7.5 centimeters, let b be the base of the glass,
applying pythagorean theorem
b² + 7.5² = 12²,
b² = 144 – 56.25 = 87.75,therefore b is square root of 87.75 is 9.36 centimeters,
Now the radius of glass is half base is 9.36/2  = 4.68 centimeters.

Question 9.
Naomi makes a lampshade by making a cone and then cutting off
part of the cone, as shown. Find the diameter of the larger opening in the lampshade.

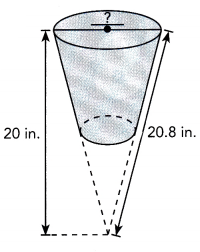
Answer:
The diameter of the larger opening in the lampshade is 5.71 in,

Explanation:
Applying pythagorean theorem let d be diameter of the
larger opening in the lampshade so d² + 20² = 20.8²,
d² = 432.64 – 400 = 32.64 ,so d is square root of 32.64 is 5.71 in.

Question 10.
Four identical pieces are cut off the sides of a cylinder, as shown. The remaining shape is a square prism. The diagonal of the prism’s square base is as long as the diameter of the cylinder. The diameter of the cylinder is 12 centimeters, and the height of the cylinder is 9 centimeters. Find the length of a side of the square base of the prism. Then find an approximate volume of the prism.

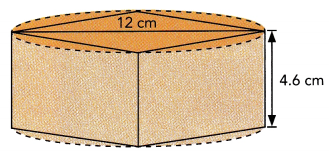
Answer:
The length of a side of the square base of the prism 3.82 cm,
Approximate volume of the prism is 67 cm³,

Explanation:
Given Four identical pieces are cut off the sides of a cylinder, as shown.
The remaining shape is a square prism. The diagonal of the prism’s
square base is as long as the diameter of the cylinder.
The diameter of the cylinder is 12 centimeters, and
the height of the cylinder is 9 centimeters.
we have Diameter of cylinder = diagonal of base of square prism
=√2 a, so a = 12/3.14 = 3.82 cm,,
now volume of prism is v = a²h = 3.82 X 3.82 X 4.6 = 67.125 cm³.

Question 11.
Ellen’s computer screen is a 20 inch screen, which means that the length of the diagonal of the rectangular screen is 20 inches. The screen can be laid flat in a box that is 12 inches wide. How long is the box?
Answer:
The box is 16 inch long,

Explanation:
Given Ellen’s computer screen is a 20 inch screen,
which means that the length of the diagonal of the rectangular screen is 20 inches.
The screen can be laid flat in a box that is 12 inches wide. Applying
pythagorean theorem let l is the length of the box so
l² + 12² = 20²,
l² = 400 -144 = 256, so length is square root of 256 is 16 inch.

Question 12.
An 18-centimeter tall suitcase is shaped like a rectangular prism. The length of the diagonal of one of its largest faces is 30 centimeters. Find the width of the suitcase.
Answer:
The width of the suitcase is 24 centimeter,

Explanation:
Given an 18-centimeter tall suitcase is shaped like a rectangular prism.
The length of the diagonal of one of its largest faces is 30 centimeters.
Let w be the width of the suitcase applying pythagores theorem
w² + 18² = 30²,
w² = 900 – 324 = 576, so width is square root of 576 is 24 centimeter.

Question 13.
Vera kicks a ball 123 feet diagonally across a rectangular playground of width 85 feet. Find the length of the playground.
Answer:
The length of the playground is 88.9 feet,

Explanation:
Given Vera kicks a ball 123 feet diagonally across a
rectangular playground of width 85 feet.
Let l be the length of the playground applying pythagorean theorem
l² + 85² = 123²,
l² = 15129 – 7225 = 7904, the value of l is square root of 7904 is 88.9 feet.

Question 14.
A river is 10.5 meters wide and its banks are parallel to each other. John tries to swim straight across, but the current pushes him downstream so that he lands 14 meters from the spot he wanted to reach. How far did he swim?
Answer:
Far did Jhon swim is 17.5 meters,

Explanation:
Given a river is 10.5 meters wide and its banks are parallel to each other.
John tries to swim straight across, but the current pushes him downstream so that he lands 14 meters from the spot he wanted to reach. Applying pythagorean theorem to find how far did he swim s is
s² = 14² + 10.5² = 196 + 110.25=306.25, the value is s square root of 306.25 is 17.5 meters.

Question 15.
An extendable ladder 9.8 feet long leans against a wall with the base 3 feet from the wall. Assuming the base of the ladder does not move, about how much higher will the top of the ladder be above the ground when the ladder extended to twice its original length?
Answer:
higher will the top of the ladder above the ground is 10.04 feet,

Explanation:
Given an extendable ladder 9.8 feet long leans against a wall with the base 3 feet from the wall and assuming the base of the ladder does not move, about how much higher will the top of the ladder be above the ground when the ladder extended to twice its original length, Let h1 is 9.8 feet and h2 is extended length is 2 X 9.8 = 19.6, Applying pythagorean theorem
h₁² =(9.8) ² -(3)²  ( For right triangle)  = 96.04 – 9 = 87.04, so h1 is square root
of 87.04 is 9.32 feet
and h₂² = (19.6)² – (3)² = 384.16 – 9 = 375.16, So h2 is the square root of
375.16 is 19.36 feet, therefore higher will the top of the ladder above
the ground is 19.36 feet – 9.32 feet = 10.04 feet.

Question 16.
A doorway is 80 inches tall and 32 inches wide. Can a round tabletop with a diameter of 90 inches fit through the doorway? If not, what is the greatest possible diameter that will fit through the doorway? Explain.
Answer:
The round tabletop does not fit through the doorway even diagonally,

Explanation:
Given a doorway is 80 inches tall and 32 inches wide,
the diagonal measure d² = 80² + 32² = 6400 + 1024 = 7424,
So d is squareroot of 7424 is 86.16 inches,
So, the round tabletop does not fit through the doorway even diagonally,
The greatest possible diameter of the round doorway is about 86 inches.