Go through the Math in Focus Grade 4 Workbook Answer Key Chapter 5 Practice 5 Probability as a Fraction to finish your assignments.
Math in Focus Grade 4 Chapter 5 Practice 5 Answer Key Probability as a Fraction
Find the probability as a fraction in simplest form.
Jake spins the spinner once. He wants to land on these numbers. What is the probability of a favorable outcome? Find the probability as a fraction in simplest form for each outcome.
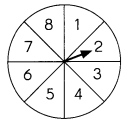
Example
He wants to land on a number less than 3.
There are 2 favorable outcomes: 1 and 2
There are 8’ possible outcomes: 1, 2, 3, 4, 5, 6, 7, and 8
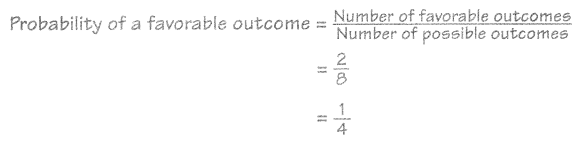
Question 1.
He wants to land on the number 7. 
Answer:
The probability of a favorable outcome is \(\frac{7}{8}\).
Explanation:
Here, the possible outcomes are \(\frac{1}{8}\),\(\frac{2}{8}\),\(\frac{3}{8}\),\(\frac{4}{8}\),\(\frac{5}{8}\),\(\frac{6}{8}\),\(\frac{7}{8}\),\(\frac{8}{8}\). As he wants to land on the number 7 it will be \(\frac{7}{8}\).
Question 2.
He wants to land on an odd number. 
Answer:
The possible outcomes are \(\frac{1}{8}\),\(\frac{3}{8}\),\(\frac{5}{8}\),\(\frac{7}{8}\).
Explanation:
Here, the possible outcomes are \(\frac{1}{8}\),\(\frac{2}{8}\),\(\frac{3}{8}\),\(\frac{4}{8}\),\(\frac{5}{8}\),\(\frac{6}{8}\),\(\frac{7}{8}\),\(\frac{8}{8}\). As he wants to land on an odd numbers so the outcomes will be \(\frac{1}{8}\),\(\frac{3}{8}\),\(\frac{5}{8}\),\(\frac{7}{8}\).
Find the probability as a fraction in simplest form for each outcome.
A coin is tossed once. The probability of getting
Question 3.
heads is 
Answer:
\(\frac{1}{2}\).
Explanation:
The probability of getting heads is \(\frac{1}{2}\).
Question 4.
tails is 
Answer:
\(\frac{1}{2}\).
Explanation:
The probability of getting tails is \(\frac{1}{2}\).
A number cube numbered 1 to 6 is tossed once. The probability of getting
Question 5.
the number 2 is 
Answer:
The probability is \(\frac{2}{6}\).
Explanation:
As the number was tossed once, so the probability of getting the number 2 is \(\frac{2}{6}\).
Question 6.
the number 0 is 
Answer:
No possible outcomes.
Explanation:
There will be no possibility of getting the number 0 as the number cube numbered 1 to 6.
Question 7.
an even number is 
Answer:
The possibilities of getting even number is \(\frac{2}{6}\),\(\frac{4}{6}\),\(\frac{6}{6}\).
Explanation:
The possible outcomes are \(\frac{1}{6}\),\(\frac{2}{6}\),\(\frac{3}{6}\),\(\frac{4}{6}\),\(\frac{5}{6}\),\(\frac{6}{6}\). So the possibilities of getting even number is \(\frac{2}{6}\),\(\frac{4}{6}\),\(\frac{6}{6}\).
Question 8.
a number greater than 4 is 
Answer:
The possibilities of getting a number greater than 4 is \(\frac{5}{6}\),\(\frac{6}{6}\).
Explanation:
The possible outcomes are \(\frac{1}{6}\),\(\frac{2}{6}\),\(\frac{3}{6}\),\(\frac{4}{6}\),\(\frac{5}{6}\),\(\frac{6}{6}\). So the possibilities of getting a number greater than 4 is \(\frac{5}{6}\),\(\frac{6}{6}\).
A circular spinner has 4 equal parts. The parts are colored red, blue, green, and yellow. The spinner is spun once. The probability of landing on
Question 9.
red is 
Answer:
The probability of landing on red is \(\frac{r}{4}\).
Explanation:
Given that a circular spinner has 4 equal parts and the parts are colored red, blue, green, and yellow and the spinner is psun once. So the probability of landing on red is \(\frac{r}{4}\).
Question 10.
blue is 
Answer:
The probability of landing on blue is \(\frac{b}{4}\).
Explanation:
Given that a circular spinner has 4 equal parts and the parts are colored red, blue, green, and yellow and the spinner is psun once. So the probability of landing on blue is \(\frac{b}{4}\).
Question 11.
purple is 
Answer:
The probability of landing on purple is \(\frac{p}{4}\).
Explanation:
Given that a circular spinner has 4 equal parts and the parts are colored red, blue, green, and yellow and the spinner is psun once. So the probability of landing on blue is \(\frac{p}{4}\).
Question 12.
green, red, or yellow is 
Answer:
The probability of landing on purple is \(\frac{p}{4}\).
Explanation:
Given that a circular spinner has 4 equal parts and the parts are colored red, blue, green, and yellow and the spinner is psun once. So the probability of landing on blue is \(\frac{p}{4}\).
Question 13.
red, blue, green, or yellow is 
Answer:
The probability of landing on red, blue, green, or yellow is \(\frac{r}{4}\), \(\frac{b}{4}\), \(\frac{g}{4}\), \(\frac{y}{4}\).
Explanation:
Given that a circular spinner has 4 equal parts and the parts are colored red, blue, green, and yellow and the spinner is psun once. So the probability of landing on red, blue, green, or yellow is \(\frac{r}{4}\), \(\frac{b}{4}\), \(\frac{g}{4}\), \(\frac{y}{4}\).
Find the probability as a fraction in simplest form for each outcome.
A bag contains 10 discs numbered 1 to 10. A disc is drawn from the bag. The probability of drawing
Question 14.
the number 10 is 
Answer:
The probability of drawing the number 10 is \(\frac{10}{10}\).
Explanation:
Here, a bag contains 10 discs numbered 1 to 10. So the probability of drawing the number 10 is \(\frac{10}{10}\).
Question 15.
a number less than 5 is 
Answer:
The probability of drawing the number 5 is \(\frac{5}{10}\).
Explanation:
Here, a bag contains 10 discs numbered 1 to 10. So the probability of drawing the number 5 is \(\frac{5}{10}\).
Question 16.
on odd number is  .
.
Answer:
The probability of drawing the odd number is \(\frac{1}{10}\), \(\frac{3}{10}\), \(\frac{5}{10}\), \(\frac{7}{10}\), \(\frac{9}{10}\).
Explanation:
Here, a bag contains 10 discs numbered 1 to 10 the probability outcomes are \(\frac{1}{10}\), \(\frac{2}{10}\), \(\frac{3}{10}\), \(\frac{4}{10}\), \(\frac{5}{10}\), \(\frac{6}{10}\), \(\frac{7}{10}\), \(\frac{8}{10}\), \(\frac{9}{10}\), \(\frac{10}{10}\). So the probability of drawing the odd number is \(\frac{1}{10}\),\(\frac{3}{10}\), \(\frac{5}{10}\), \(\frac{7}{10}\), \(\frac{9}{10}\).
Question 17.
a number divisible by 3 is 
Answer:
The probability of drawing the number divisible by 3 is \(\frac{3}{10}\), \(\frac{6}{10}\), \(\frac{9}{10}\).
Explanation:
Here, a bag contains 10 discs numbered 1 to 10 the probability outcomes are \(\frac{1}{10}\), \(\frac{2}{10}\), \(\frac{3}{10}\), \(\frac{4}{10}\), \(\frac{5}{10}\), \(\frac{6}{10}\), \(\frac{7}{10}\), \(\frac{8}{10}\), \(\frac{9}{10}\), \(\frac{10}{10}\). So the probability of drawing the number divisible by 3 is \(\frac{3}{10}\), \(\frac{6}{10}\), \(\frac{9}{10}\).
Question 18.
a number greater than 8 is 
Answer:
The probability of drawing the number greater than 8 is \(\frac{9}{10}\), \(\frac{10}{10}\).
Explanation:
Here, a bag contains 10 discs numbered 1 to 10 the probability outcomes are \(\frac{1}{10}\), \(\frac{2}{10}\), \(\frac{3}{10}\), \(\frac{4}{10}\), \(\frac{5}{10}\), \(\frac{6}{10}\), \(\frac{7}{10}\), \(\frac{8}{10}\), \(\frac{9}{10}\), \(\frac{10}{10}\). So the probability of drawing the number greater than 8 is \(\frac{9}{10}\), \(\frac{10}{10}\).
Question 19.
the number 12 is  .
.
Answer:
There is no possibility of drawing number 12
Explanation:
Here, a bag contains 10 discs numbered 1 to 10 the probability outcomes are \(\frac{1}{10}\), \(\frac{2}{10}\), \(\frac{3}{10}\), \(\frac{4}{10}\), \(\frac{5}{10}\), \(\frac{6}{10}\), \(\frac{7}{10}\), \(\frac{8}{10}\), \(\frac{9}{10}\), \(\frac{10}{10}\). So there is no possibility of drawing number 12.
A bag contains 3 white marbles, 3 blue marbles, and 6 red marbles. A marble is drawn from the bag. The probability of getting
Question 20.
a white marble is 
Answer:
The probability of getting a white marble is \(\frac{3}{12}\).
Explanation:
Given that a bag contains 3 white marbles, 3 blue marbles, and 6 red marbles. So the total number of marbles are 3+3+6 which is 12 marbles. So the probability of getting a white marble is \(\frac{3}{12}\).
Question 21.
a blue marble is 
Answer:
The probability of getting a blue marble is \(\frac{3}{12}\).
Explanation:
Given that a bag contains 3 white marbles, 3 blue marbles, and 6 red marbles. So the total number of marbles are 3+3+6 which is 12 marbles. So the probability of getting a white marble is \(\frac{3}{12}\).
Question 22.
Which is more likely: drawing a red marble or drawing a blue marble? Explain.
Answer:
Red marbles.
Explanation:
As there are 3 white marbles, 3 blue marbles, and 6 red marbles. So the more likely drawing marble will be red marbles.
Find the probability of each outcome on the number line. Then describe the outcome as more likely, less likely, certain, impossible, or equally likely.
Example
A box contains 4 red pencils, 1 blue pencil, and 1 black pencil. Find the probability of picking a red pencil.
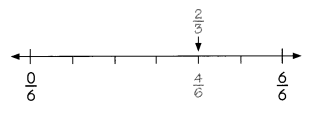
The closer the probability of an outcome is to 1, the more likely the outcome is to occur.

The probability of picking a red pencil is \(\frac{4}{6}\) or \(\frac{2}{3}\)
\(\frac{2}{3}\) is closer to 1 than to 0 on the number line, So, the likelihood of picking a red pencil is more likely.
Each card in a set of 8 cards has a picture of a fruit. There are 3 orange cards, 2 apple cards, 2 pear cards, and 1 peach card. The cards are shuffled, placed in a stack, and one card is picked.

Question 23.
An orange card: ____
Answer:
The probability of picking the orange card is \(\frac{3}{8}\).
Explanation:
Given that each card in a set of 8 cards has a picture of a fruit and there are 3 orange cards, 2 apple cards, 2 pear cards, and 1 peach card. So the probability of picking the orange card is \(\frac{3}{8}\).
Question 24.
An apple card: ____
Answer:
The probability of picking the apple card is \(\frac{2}{8}\).
Explanation:
Given that each card in a set of 8 cards has a picture of a fruit and there are 3 orange cards, 2 apple cards, 2 pear cards, and 1 peach card. So the probability of picking the apple card is \(\frac{2}{8}\).
Question 25.
An apple, peach, or pear card: ____
Answer:
The probability of picking an apple, peach, or pear card \(\frac{2}{8}\), \(\frac{1}{8}\), \(\frac{2}{8}\).
Explanation:
Given that each card in a set of 8 cards has a picture of a fruit and there are 3 orange cards, 2 apple cards, 2 pear cards, and 1 peach card. So the probability of picking an apple, peach, or pear card \(\frac{2}{8}\), \(\frac{1}{8}\), \(\frac{2}{8}\).
Question 26.
An apple, orange, peach, or pear card: ____
Answer:
The probability of picking an apple, peach, or pear card\(\frac{2}{8}\), \(\frac{3}{8}\), \(\frac{1}{8}\) and \(\frac{2}{8}\).
Explanation:
Given that each card in a set of 8 cards has a picture of a fruit and there are 3 orange cards, 2 apple cards, 2 pear cards, and 1 peach card. So the probability of picking an apple, orange, peach, or pear card \(\frac{2}{8}\), \(\frac{3}{8}\), \(\frac{1}{8}\) and \(\frac{2}{8}\).