Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 8 Lesson 8.2 Reflections to score better marks in the exam.
Math in Focus Grade 7 Course 3 B Chapter 8 Lesson 8.2 Answer Key Reflections
Math in Focus Grade 8 Chapter 8 Lesson 8.2 Guided Practice Answer Key
Solve.
Question 1.
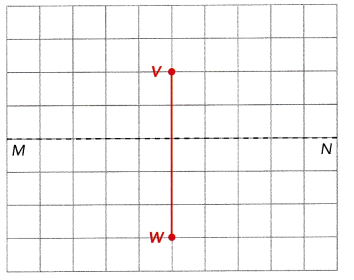
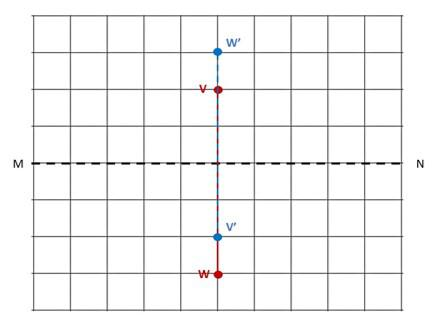
Andrew wants to hang a square poster on his bedroom wall. He knows that to get the poster to balance properly, he needs to place a second picture hanger at W’, with the dotted vertical line as the line of symmetry. If the distance between W and the vertical line is 3 inches, find WW’.
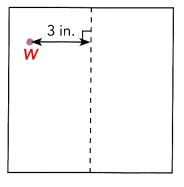
Answer:
W’ is the reflection of W so if W is 3 inches from the vertical then W’ is also 3 inches away from the vertical line. Thus WW’is the sum of the length of W and the length of W’. Therefore, WW’ is 6 inches.
Technology Activity
Explore The Properties Of Reflections With Geometry Software
Step 1.
Draw a vertical line segment using a geometry software program.
Step 2.
Select the y-axis as the line of reflection. Reflect the line segment. How are the line and its image related to the line of symmetry?
Step 3.
How are the lengths of the segment and its image relate?
Step 4.
Repeat Step 1 to Step 3 first using a horizontal segment and then a segment that is neither vertical nor horizontal.
Step 5.
Repeat Step 1 to Step 4 using the x-axis as the line of reflection.
Step 6.
Draw a rectangle and reflect it over the y-axis. Do the parallel lines of the rectangle stay parallel? Do the perpendicular sides of the rectangle stay perpendicular?
Step 7.
Repeat Step 6 using the x-axis as the line of reflection.
Math Journal Which of these properties does a reflection seem to preserve: length, shape, parallel lines, or perpendicular lines? Explain.
Draw Images After Reflections.
In the activity, you may have observed the following:
Reflections preserve shape and size. They also preserve parallelism and perpendicularity.
All polygons and combinations of polygons are made up of line segments joined at their endpoints. When you reflect these figures, you reflect all the line segments joined at their endpoints. The images of all these line segments and their endpoints combine to form the whole image.
Copy and complete on graph paper.
Question 2.
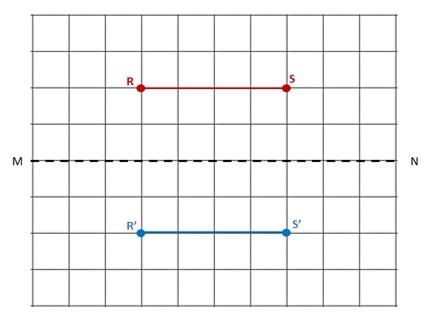
Each line segment is reflected in \(\overleftrightarrow{M N}\). On a copy of the diagram, draw each image.
a)
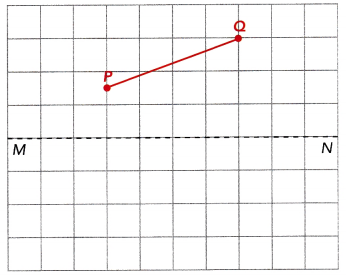
Answer:
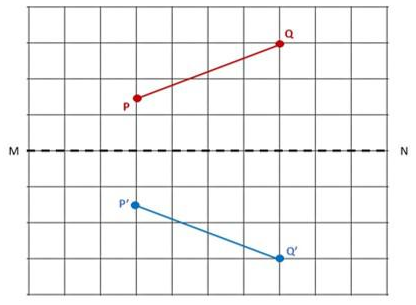
b)
Answer:
c)
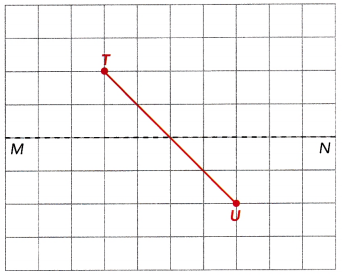
Answer:
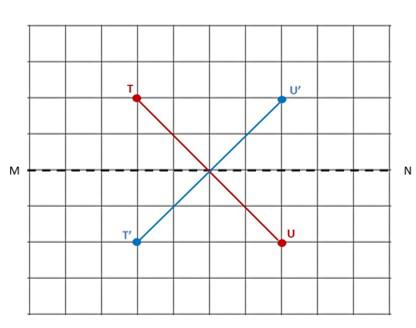
d)
Answer:
Copy and complete on graph paper.
Question 3.
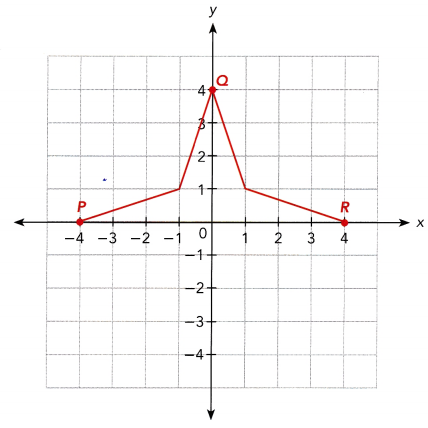
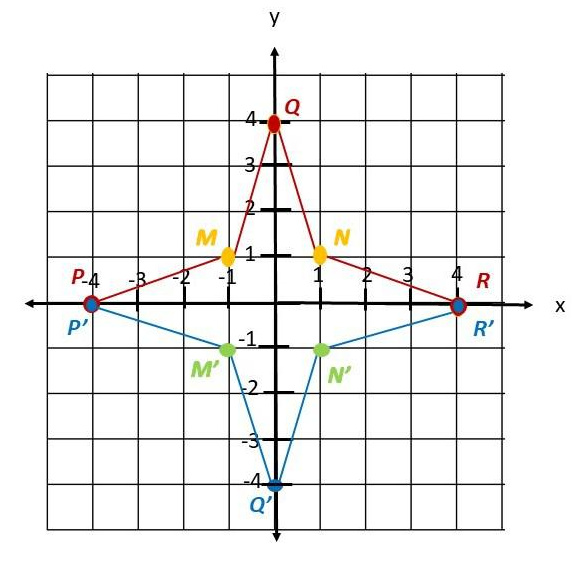
Layla is designing a star-shaped figure for a stencil. She wants the bottom half to be a reflection of the top half. She will reflect it across the x-axis to draw the other half. Complete the design for her.
Answer:
P(-4, 0), Q(0, 4) and R(4, 0) are plotted on the plot. Put additional points M and N on the coordinates (-1, 1) and (1, 1) to make the plotting easier. Since the reflection is in the x-axis then all the coordinates will not change. For P(-4, 0) and R(4, 0), since 0 is 0 units away from x then for image P’ and R’ will be along the x-axis with coordinates (-4, 0) and (-4, 0) respectively. Point Q(0, 4) on the other hand is 4 units above the x-axis so its R’ units below the axis. For M(-1, 1) and N(1, 1)since it is 1 unit above the x-axis then their image will be 1 unit beneath that axis. Thus M’ will be on (-1, 1) and N’ will be on (1, -1).
Complete.
Question 4.
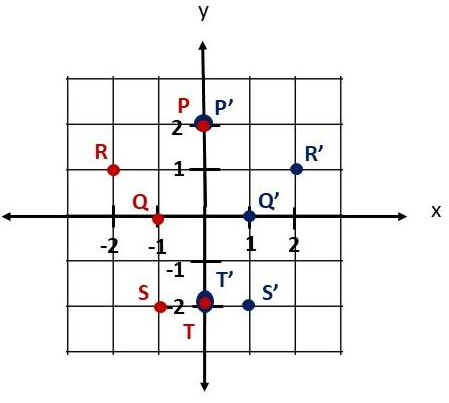
A figure has vertices P (0, 2), Q (-1, 0), R (-2, 1), S (-1, -2), and T (0, -2), is reflected in the y-axis. Draw the figure and its image on the coordinate plane. Use 1 grid square on both axes to represent 1 unit for the interval from -2 to 2.
Answer:
Complete.
Question 5.
Mr. Patterson is building a double bird house, one next to the other. The vertices of the front of one houses have coordinates P (3, 0), Q (5, 3), R (3, 6), and S (1, 3).
The front of the other bird house, P’Q’R’S’, is a reflection of the first one in the y-axis.
The x-coordinates of vertices of PQRS and P’Q’R’S’ are ![]() , and their y-coordinates are
, and their y-coordinates are ![]() .
.
P(3, 0) is mapped onto P'(![]() ,
, ![]() ).
).
Q (5, 3) is mapped onto Q’ (![]() ,
, ![]() ).
).
R (3, 6) is mapped onto R’ (![]() ,
, ![]() ).
).
S (1, 3) is mapped onto S’ (![]() ,
, ![]() ).
).
Any point (x, y) is mapped onto (![]() ,
, ![]() ) when reflected in the y-axis.
) when reflected in the y-axis.

Answer:
The x-coordinates of vertices of PQRS and P’Q’R’S’ are negative of each other and their y-coordinates are did not change.
P(3, 0) is mapped onto P'(-3, 0).
Q (5, 3) is mapped onto Q’ (-5, 3).
R (3, 6) is mapped onto R’ (-3, 6).
S (1, 3) is mapped onto S’ (-1, 3).
Any point (x, y) is mapped onto (-x, y) when reflected in the y-axis
Math in Focus Course 3B Practice 8.2 Answer Key
Copy each diagram on graph paper and draw the image using the given reflection.
Question 1.
In the x-axis
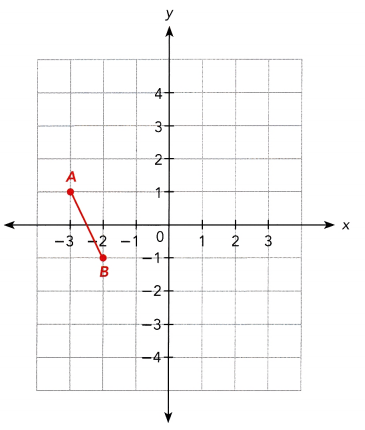
Answer:
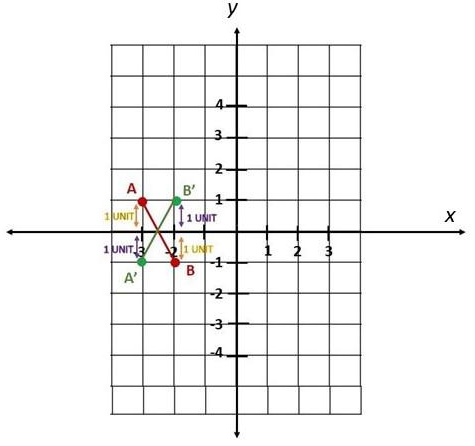
Question 2.
In the y-axis
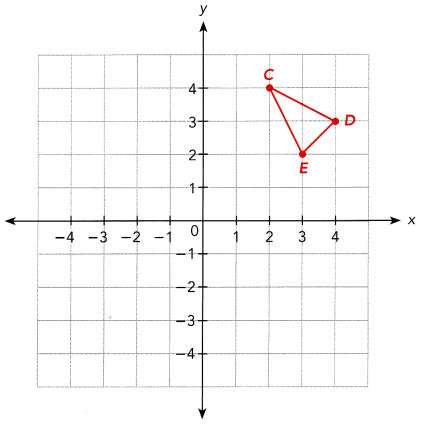
Answer:
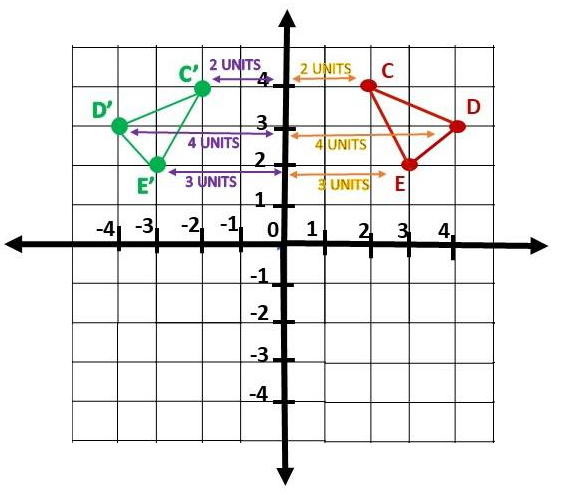
Question 3.
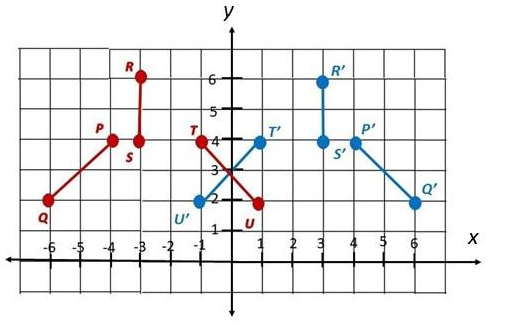
Ethan placed six sticks on a table. Three of the sticks, \(\overline{P Q}\), \(\overline{R S}\), and \(\overline{T U}\) are shown on the coordinate plane. The other sticks are images of the three sticks, with x = 0 as the line of reflection. On a copy of the graph, draw the sticks not shown on the coordinate plane.
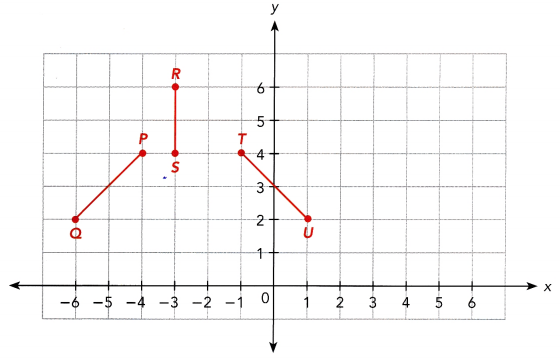
Answer:
Solve.
Question 4.
A pattern is drawn on the coordinate plane and then repeated by first reflecting it in the x-axis and reflecting the original pattern in the y-axis.
a) Copy and complete the table by finding the position of each of the other tiles. On a copy of the coordinate plane, indicate the positions of the images.
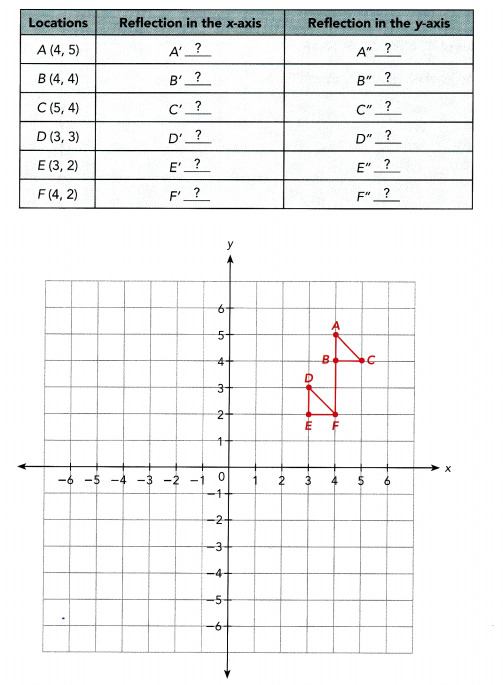
Answer:
Note that if A, B, C, D, E, and Fis reflected in x-axis, the coordinates wiLl be in the form (x, -y) while the image after applying the reflection in y-axis has coordinates in the form (-x, y) then and in the coordinate plane.
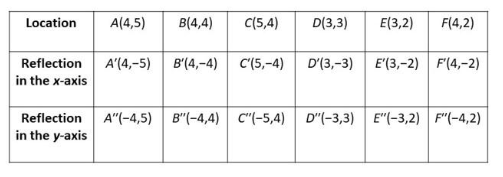
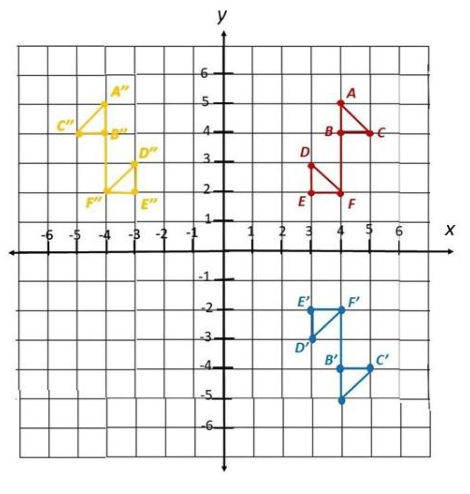
b) Reflect A’, B’, and C’ in the y-axis. What are the coordinates of the image?
Answer:
If A’, B’, and C’ is reflected in y-axis, the coordinates wiLL be in the form (-x, y) then the ¡mage of A’(4, -5) will be on (-4, -5), B’(4, -4) will have an image on (-4, -4) and the image of C’(5, -4) will be plotted on (-5, -4).
c) Reflect A”, B”, and C” in the x-axis. What are the coordinates of the image? How do these coordinates compare to those in b)?
Answer:
If A”,B”, and C” ¡s refLected in x-axis, the coordinates will be in the form (x, -y) then the images of A”(-4, 5), B”(-4, 4), and C”(-5, 4) will be on (-4, -5), (-4, -4) and (-5, -4). Observe that A’, B’, and C’ if reflected in y-axis has the same image with A”, B”, and C” if it is reflected in x-axis.
Copy and complete on graph paper.
Question 5.
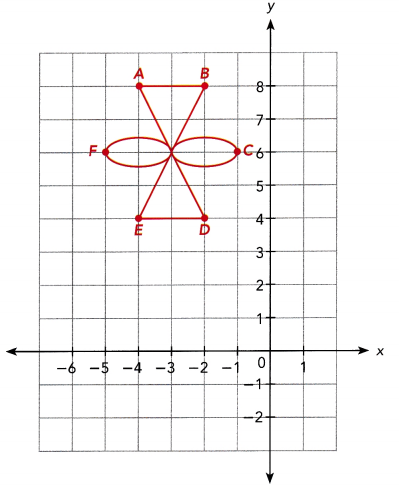
Isabella painted a water color design on graph paper. Some of the points were at A (-4, 8), 8 (-2, 8), C(-1, 6), D (-2, 4), E (-4, 4), and F(-5, 6). She folded the paper along y = 3 to reflect the design.
The image points are A’, 8′, C’, D’, E’, and F’.
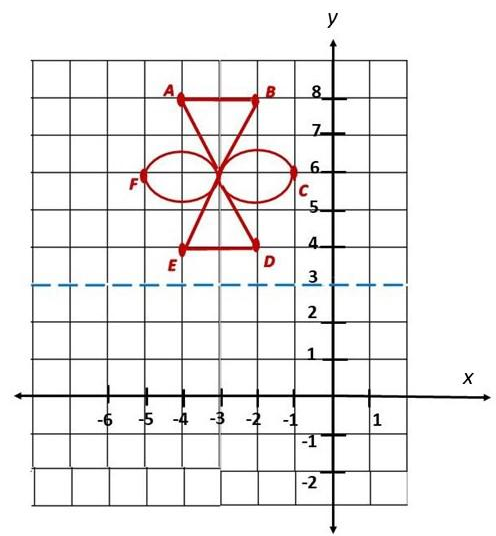
a) Draw the line y = 3.
Answer:
The line y equals to 3 is a line segment whose coordinates are (0,3) then
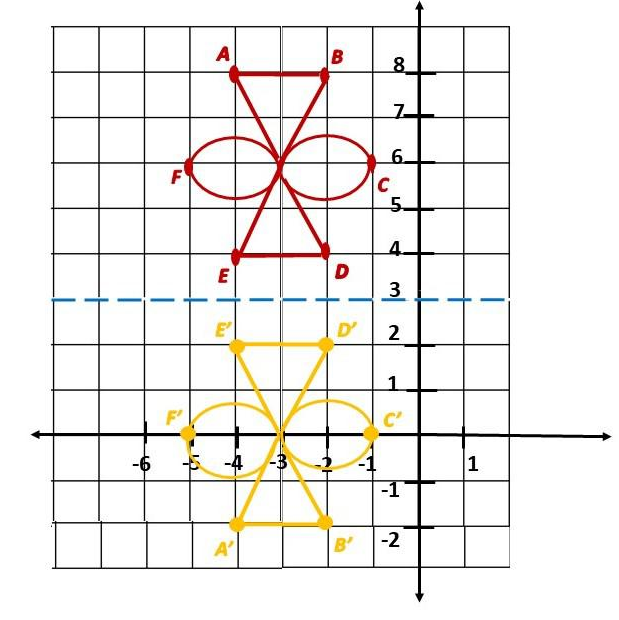
b) Find the coordinates of A’, B’, C’, D’, E’, and F’.
Answer:
A coordinates are (-4, 8) first know the position of the point on the coordinate plane. Notice that A is 5 units above y = 3, so the y coordinate for the image A is 5 units below y = 3 which is -2. Therefore, the coordinates of A’ is (-4 ,-2).
B coordinates are (-2, 8) first locate the point on the coordinate plane. Notice that B is 5 units above y = 3, so the y coordinate for the image B is 5 units below y = 3 which is -2. Therefore, the coordinates of A’ is (-2, -2).
Locating C(-1, 6) observe that C is 3 units above y = 3 then, y coordinate for the image C is 3 units under y = 3 which is 0. Therefore, the coordinates of C’ is (-1, 0).
For D whose coordinates are (-2, 4), the first step is to locate the point notice that D is 1 unit above y = 3 so the y coordinate for the image of D is 1 unit below y = 3 which is 2. Therefore, the coordinates of D’ is (-2, 2).
Determine the position of E (-4, 4) note that E is 1 unit above y = 3 thus, the y coordinate for the image of E is 1 unit beneath y = 3 which is 2. Therefore, the coordinates of E’ is (-4, 2).
Lastly, Locate F(-5, 6). Observe that F is 3 units above y = 3 then, the y coordinate for the image of F is 3 units under y = 3 which is 0 . Therefore, the coordinates of F’ is (-5, 0).
c) Draw the image and label A’, B’, C’, D’, E‘, and F’.
Answer:
Solve.
Question 6.
The image of a butterfly with its wings symmetrically spread out is outlined on the coordinate plane. The uppermost tips of the wings are at (4, 5) and (-2, 5). The lower most tip of one wing is at (2, 0).
a) Find an equation of the line of reflection.
Answer: Plot the points on the coordinate plane. Let these points (4, 5) and (-2, 5) be an original point and its image. The y coordinates did not change, the reflection must be in x. Also, they are 6 points away from each other, the points are 3 units away from x = 1. Since the line of reflection is exactly in between the original point and its image, therefore, the line of reflection for this case is x =1.
b) Find the position of the lower tip of the other wing.
Answer: The line of reflection x = 1, let (2, 0) be an original point and the image be the point where the last tip of the wing is. Observe that the line of reflection is a vertical line then the image of (2, 0) will be on the same horizontal line where (2, 0). Next, the original point is 1 unit away from the line of reflection thus its image is 1 unit from the opposite side of x =1. Therefore, on the same horizontal line, move 1 unit to the left the line of reflection, the other tip of the wings is on (0, 0).
Question 7.
Math Journal Point A’ is the image of point A under a reflection. How do you find the line of reflection, without the use of a coordinate grid?
Answer: The reflection of A has the same distance from the line of reflection. Therefore, the line of reflection can be determined by adding the lengths of the original point and the image then dividing the sum by 2. Their midpoint must be the line of reflection.
Question 8.
A tablecloth has two red dots on it. They are at positions (-3, -1) and (-1, -3). The cloth is folded in half, so that the dots touch each other. What is an equation for the line along which the tablecloth was folded?
Answer:
x = y
The point (-2,-2) is the reflection of the points (-3,-1) and (-1,-3) since it is exactly in between the points. Both are 1 diagonal unit away from the point. Thus, the diagonal line whose points are (-3,-3),(-2,-2),(-1,-1)is the line of reflection of the points. When y is 1, x is equal to 1, if y is equal to 2 x is 2.
Question 9.
A leaf is symmetric about its midvein, the central vein that runs the length of the leaf. The leaf is outlined in the coordinate plane with its midvein on the line y = -x.
a) A side vein has a length of 6 units on the grid. What is the length of its symmetric counterpart?
Answer:
6 units
The line of reflection is exactly in the middle of the original point or line and its image. If the original points or lines are 10 units away from the line of reflection, then so is the image, if it is 1 unit away, then so is their reflection. Let the side vein be the original line, the grid be the reflection of the line and the image be the symmetric counterpart of the vein. From the above explanation, since the original line is 6 units away from the grid then the image is also 6 units away.
b) The endpoint of another side vein is at (4, 3). What is the endpoint of its symmetric counterpart?
Answer: (-3,-4)
Explanation:
The line of reflection according to its equation is a diagonal line. Plotting (4,3) notice that the point is 3 and a half diagonal units from the line of reflection thus its image also has the same distance on the opposite side. So from the line of reflection, move 3 and half diagonal units. Therefore, the endpoint of the corresponding symmetric side of the vein is (-3,-4).