Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 8 Lesson 8.3 Rotations to score better marks in the exam.
Math in Focus Grade 7 Course 3 B Chapter 8 Lesson 8.3 Answer Key Rotations
Math in Focus Grade 8 Chapter 8 Lesson 8.3 Guided Practice Answer Key
Solve. Show your work.
Question 1.
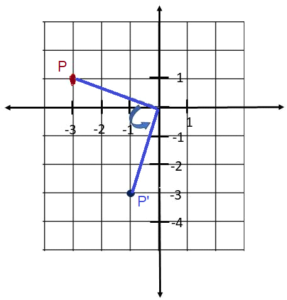
P is rotated counterclockwise to P’ about the origin. State the angle of rotation.
a)
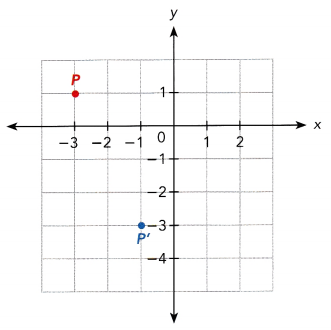
Answer:
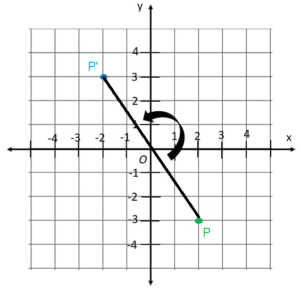
b)
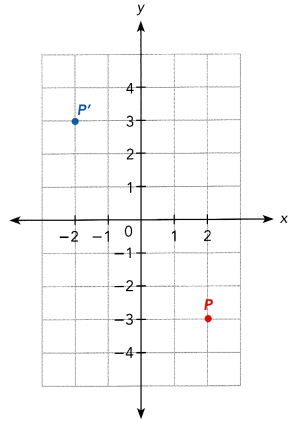
Answer:
Question 2.
The tip of a fan blade for a ceiling fan rotates from position W to W. The angle of rotation is 180°.
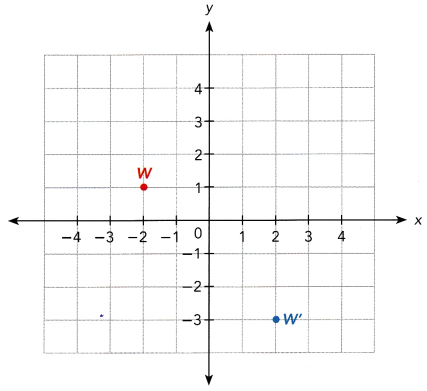
Answer:
A 180° rotation is also called a half turn. You do not have to include the direction of rotation for half-turn, because 180° clockwise is the same as 180° counterclockwise.

a) On a copy of the graph, mark and label the center of rotation as T.
Answer:
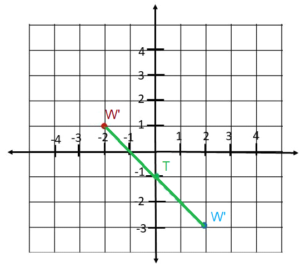
T = (x1+x2 / 2, y1+y2 / 2)
T = (-2 + 2/2, 1+(-3) / 2)
T = (0/2, -0/2)
T = (0, -1)
Therefore, the centre of rotation T has a coordinate (0, -1)
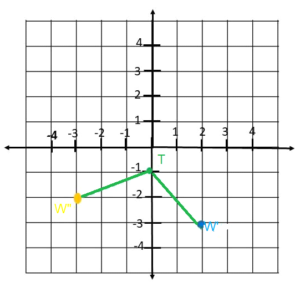
b) W’ is rotated 90° clockwise to W” about the center T. Label W” on the graph in a).
Answer:
Complete.
The hour hand of a clock turns through an angle from 12 noon to 4 P.M. State the following.
a) The center of rotation
Answer: The hands of the clock are placed on the center while moving from 12 to 4. While undergoing a rotation, this point where the other end of the hands does not move. Thus the center of the rotation is the center of the clock.
b) The angle and direction of rotation
Answer: The complete rotation of the hands of the whole clock is 360°. The clock is divided into 12 representing the 12 hours. By dividing 360° to 12, then for every hour the hand of the clock rotates at an angle of 30°. Thus, turning from 12 to 4, then the angle of rotation of the hand of the clock is 120°. Also, the hand moves from left to right direction then the rotation is in a clockwise direction.
Technology Activity
Explore The Properties Of Rotations With Geometry Software
Materials:
- geometry software
Step 1.
Draw a line segment AB using a geometry software program.
Step 2.
Select the Rotate function, within the Transform menu. Enter 90° to rotate \(\overline{A B}\) counterclockwise about the origin. Call the image \(\overline{A^{\prime} B^{\prime}}\).
Step 3.
Make a table of coordinates for the segment endpoints and their images. How are the lengths of the two segments related?
Step 4.
Rotate \(\overline{\mathrm{AB}}\) 90° clockwise by changing the angle of rotation to -90°. Call this image \(\overline{A^{\prime \prime} B^{\prime \prime}}\). Repeat the activity in Step 3.
Step 5.
Choose a different angle of rotation and rotate \(\overline{\mathrm{AB}}\) once again. Repeat . How do the lengths of \(\overline{\mathrm{AB}}\) and \(\overline{A^{\prime} B^{\prime}}\) compare?
Step 6.
Repeat Step 2 to Step 5 using a rectangle as the original figure. Observe how the image is related to the original rectangle.
Math Journal Which of these properties does a rotation seem to preserve: length, shape, parallel lines, or perpendicular lines? Explain.
Draw images after rotations about the origin.
In the activity, you may have observed the following:
Rotations preserve shape and size. They also preserve parallelism and perpendicularity.
You have seen how a line segment can be rotated. A rotation can be described as a transformation that rotates all points on a line or figure clockwise or counterclockwise angle about the center of rotation. You will see in the next example how to find the image of a figure after a rotation.
Copy and complete on graph paper.
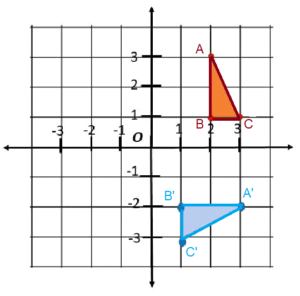
Question 4.
A rotation of ∆ABC 90° clockwise about the origin, O, produces the image ∆A’B’C’. Draw and label the image ∆A’B’C’.
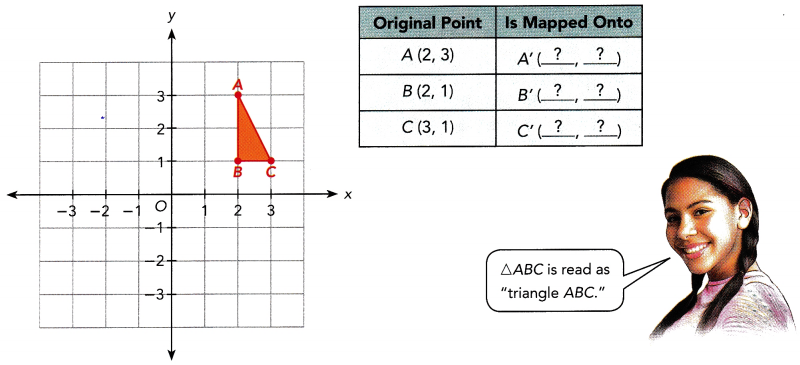
Answer:

Copy and complete on graph paper.
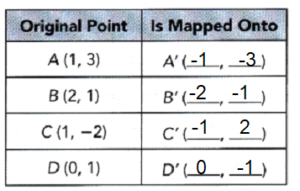
Question 5.
An animation artist draws a fish on the coordinate plane and marks the points A, B, C, and D. Then the artist rotates the fish 180° about the origin, O. Complete the table of coordinates to show the coordinates of the image points A’, B’, C’, and D’.
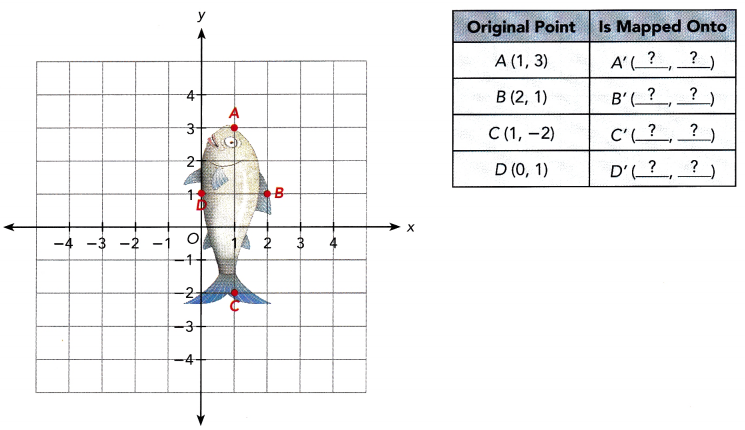
Answer:
Question 6.
DEFG is rotated 90° counterclockwise about O.
a) Draw and label the image D’E’FG’.
Answer:
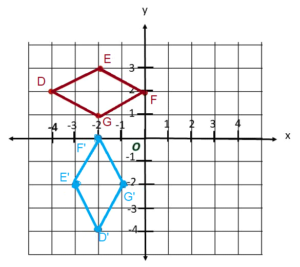
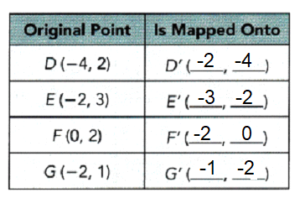
b) Complete the table of coordinates for DEFG and its image D’E’F’G’.
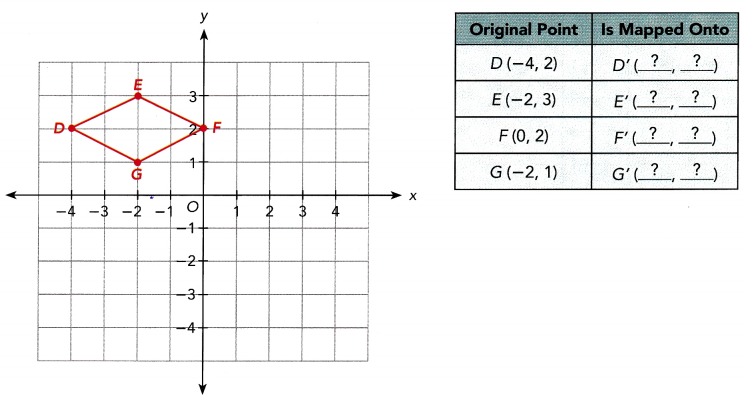
Answer:
Math in Focus Course 3B Practice 8.3 Answer Key
Solve. Show your work.
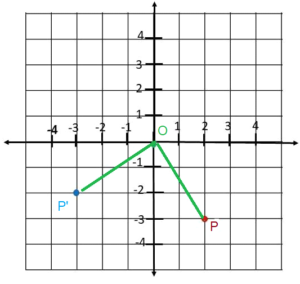
Question 1.
A rotation of point P clockwise about O maps onto P’. State the angle of rotation.
a)
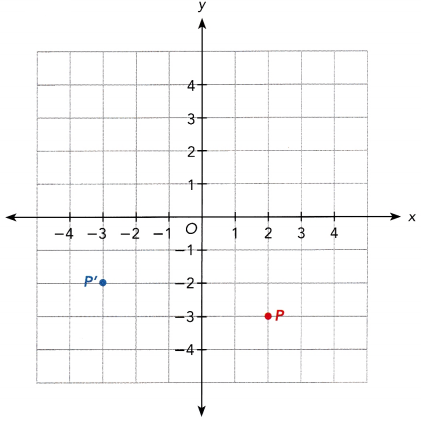
Answer:
b)
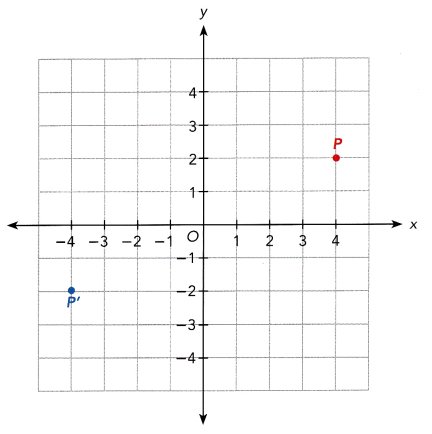
Answer:
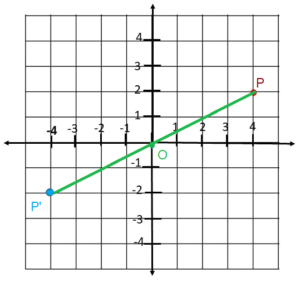
Question 2.
\(\overline{O N}\) is rotated about the origin, O to form the image \(\overline{O N^{\prime}}\). State the angle and direction of each rotation.
a)
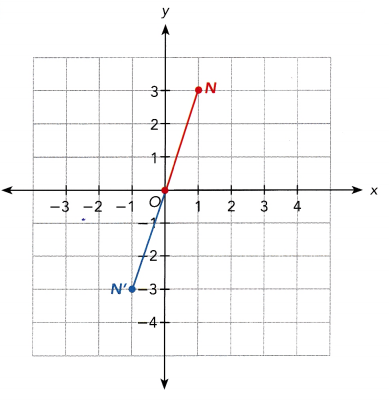
Answer:
The point N is on (1,3), N’ is on (-1,-3) and the point of rotation is point O. The line created from N to O and O to N’ is a straight line and has an angle of 180°. To ensure the angle of rotation is 180°, the coordinates should have changed from (x,y) to (-x,-y). Since N is on (1,3) and its image N’ is on (-1,-3) then the angle of rotation is indeed 180°.
b)
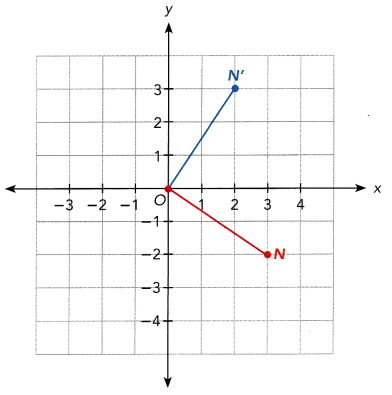
Answer:
The point N is on (3, -2), N’ is on (2, 3) and the point of rotation is point O. The lines created from P to O and O to P’ makes a right angle. To ensure that the angle of rotation is 90° counterclockwise, the coordinate should have changed from (x, y) to (-y, x). Since N is on (3, -2) and its image N’ is on (2, 3) then the angle of rotation is indeed 90° in a counterclockwise direction.
Solve. Show your work.
Question 3.
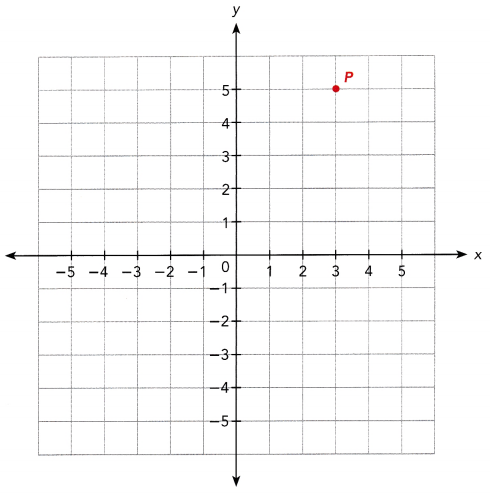
At an amusement park, Olivia is riding the carousel at point P. She is rotated from P by each of the following rotations. Mark and label her position after each rotation from P on a copy of the graph.
a) A: 90° counterclockwise about the origin
Answer: P is at (3, 5). The rotation at 90° counterclockwise changes the coordinates from (x, y) to (-y, x). Therefore, Olivia at (3, 5) will be on point A(-5, 3) when the carousel rotates at this degree and at this direction.
b) B : 90° clockwise about the origin
Answer: The rotation at 90° clockwise shifts the coordinates from (x, y) to (y, -x). So Olivia at (3, 5) will be at B (5, -3) after the rotation at this angle and in this direction.
c) C: 270° counterclockwise about the origin
Answer: A 270° rotation counterclockwise is basically just a 180° plus 90° counterclockwise direction. A 180° angle of rotation moves the coordinates from (x, y) to (-x, -y). Thus, P(3, 5) will be on (-3,-5). Then rotating it again 90°counterclockwise, the new point should be at the form (-y, x). Therefore, Olivia will be on C(5, -3) after this rotation at this direction.
d) D: Half turn about the origin
Answer:
Answer:
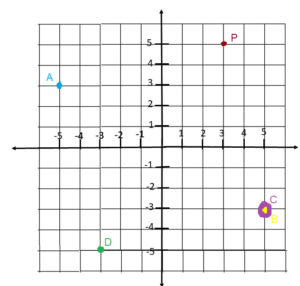
Question 4.
A cam of an automobile rotates about a shaft at the origin, O. Point P on the cam rotates to point Q.
a) Describe the rotation.
Answer: The point is on (2, 2) and Q is on (-2, 2). The coordinate (x, y) shifted to (-y, x). Therefore, the angle of rotation is 90° counterclockwise direction because the coordinates changed from (x, y) to (-y, x).
b) A point (-5, 4) undergoes the same rotation. Find the coordinates of the image.
Answer: (-5,4) is rotated counterclockwise at 90° then the coordinates (x, y) should shift to (-y, x). Therefore, the image of (-5, 4) will have the coordinates (-4, -5).
Question 5.
The hinges on a door are at (0, 0), looking down from above. Its keyhole is at position (2, 4) when the door is closed. The door swings open. Find the position of the keyhole under each rotation below.
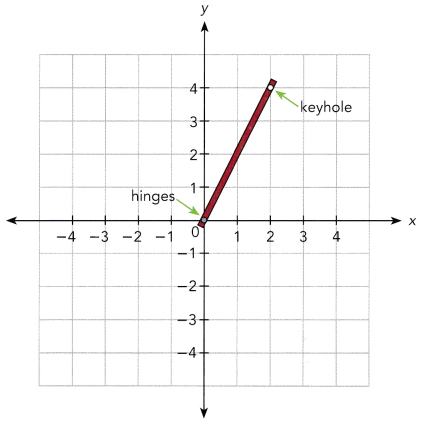
a) 90° clockwise
Answer: The point is on (2,4) should changed from (x, y) to (-y, x) for 90° clockwise rotation. Therefore, the keyhole at (2, 4) will be on point (4,-2) when the door is open 90° clockwise.
b) 90°counterclockwise
Answer: (2, 4) is rotated counterclockwise at 90° then the coordinates (x, y) should shift to (-y, x). Therefore, the keyhole at (2, 4) will have the coordinates (4, -2) when the door is open 90° clockwise.
c) 180°
Answer: Point (2, 4) has a 180° angle of rotation then the coordinates should have changed from (x, y) to (-y, x). Therefore, the keyhole at (2, 4) will have the coordinates from (-2, -4) when the door is open rotates 180°.
Question 6.
Pentagon ABCDE is drawn on the coordinate plane.
a) ABCDE is rotated 90° clockwise about the origin, O. Draw and label the image A’B’C’D’E’.
Answer:
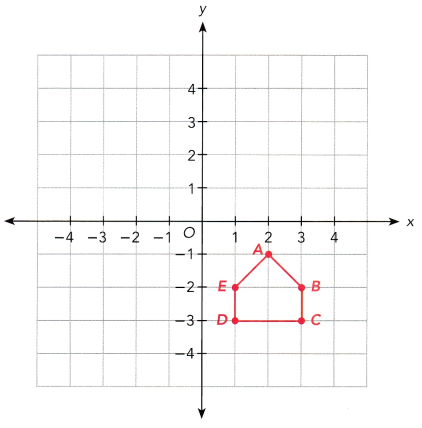
b) State the coordinates of A’, B’, C’, D’, and E’.
Answer: The rotation changes the coordinates from (x,y) to (y,-x). Thus, the coordinates of points A’, B’, C’, D’ and E’ are (-1, -2), (-2, -3), (-3, -3), (-3, -1) and (-2, -1) respectively.
c) ABCDE is rotated 90° counterclockwise about the origin, O. Draw the image A”B”C”D”E”. State the coordinates for A”B”C”D”E”.
Answer: A 90° rotation counterclockwise direction changes the coordinates (x,y) to (-y,x). Thus, A at (2,-1) will have an image A” at (1, 2), B(3, -2) will be mapped onto B”(2, 3), C at (3, -3) will have an image C” at (3, -3) D(1, -3) will be mapped onto D”(3, 1) and E at (1, -2) will have an image E” at (2, 1). So, plotting the points of the images, A”, B”, C”, D”, E”.
d) How are A’B’C’D’E’ and A”B”C”D”E” related?
Answer: The coordinates of points A’B’C’D’E’ are (-1, -2), (-2, -3), (-3, -3), (-3,-1) and (-2, -1) respectively while the coordinates of points A”B”C”D”E” (1, 2), (2, 3), (3, 3), (3, 1) and (2, 1) respectively. On the other hand, the 180° rotation changes the coordinates from (x, y) to (-x, -y) which is the case if pentagon A’B’C’D’E’ will be the original figure and the image will be A”B”C”D”E”. Therefore A”B”C”D”E” is the image of A’B’C”D’E’ if it is rotated at an angle of 180°.
Question 7.
A regular hexagon ABCDEF is rotated about its center, O, so that its appearance stays the same, but the vertices are rotated to different positions. For example in one rotation, A moves to B, B to C, and so on. Which clockwise rotations will cause this effect? Which points are invariant under a rotation? Explain.
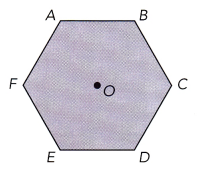
Answer: A whole hexagon has a complete angle of 720°. The figure has 6 equal angles, dividing 720° to 6 than a angle to angle rotation has 120° which is the case in this problem. Therefore, the angle of rotation is 120°.
Question 8.
Math Journal Which points are invariant under a rotation? Explain.
Answer: The points that are invariant are those that did not change even after the rotation. If a point or line or figure is rotated at any angle at any direction about (0, 0) then the invariant is (0, 0) since this point will not change at any rotation the point or line or figure will undergo. If it is rotated at about (1, 2) then the invariant is (1, 2). Therefore, the centers of rotation are the invariant points.