Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 6 Lesson 6.4 Interior and Exterior Angles to score better marks in the exam.
Math in Focus Grade 7 Course 2 B Chapter 6 Lesson 6.4 Answer Key Interior and Exterior Angles
Math in Focus Grade 7 Chapter 6 Lesson 6.4 Guided Practice Answer Key
Hands-On Activity
Materials:
- scissors
- ruler
Explore The Sum Of The Angles In A Triangle
Work in pairs.
Step 1.
Draw and cut out a triangle. Label the three angles of the triangle as 1, 2, and 3.
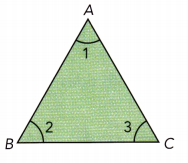
Step 2.
Cut the triangle into three pieces, so that each piece contains a vertex.
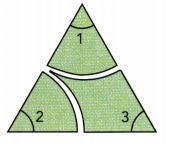
Step 3.
Rearrange the cut pieces on a straight line. What do you notice about the sum of the measures of the three interior angles?
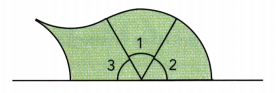
Complete.
Question 1.
Find the value of p.
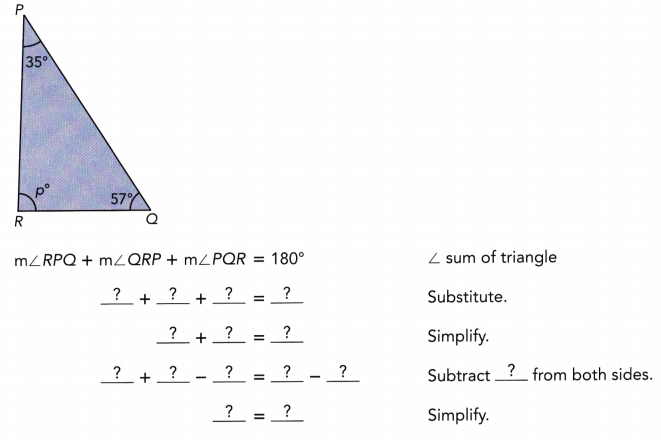
Answer:
p° = 88°
Explanation:
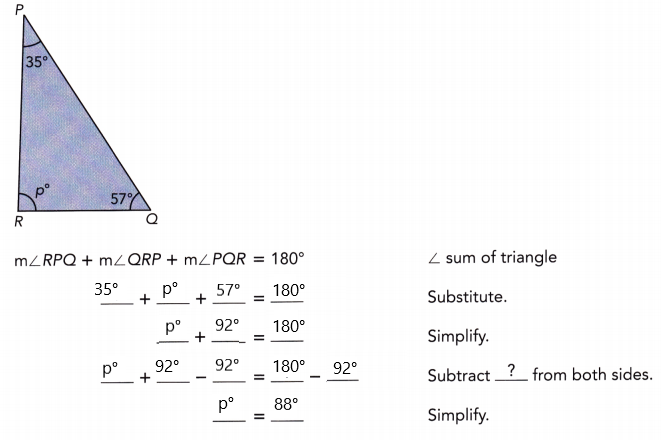
∠RPQ + ∠QRP + ∠PQR = 180°
35° + p° + 57° = 180°
p° + 92° = 180°
p° = 180° – 92°
p° = 88°
Complete.
Question 2.
Triangle XYZ is an isosceles triangle and m∠XYZ = 55°. Find the value of x.
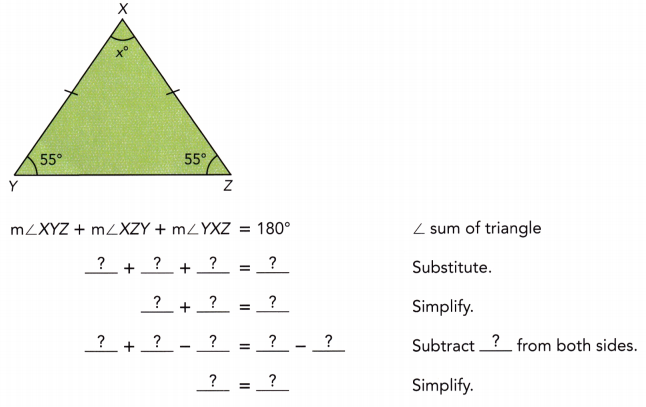
Answer:
∠XYZ + ∠XZY + ∠YXZ = 180°
55° + 55° + x° = 180°
110° +x° = 180°
x° = 180° – 110°
x° = 70°
Find the value of each variable.
Question 3.
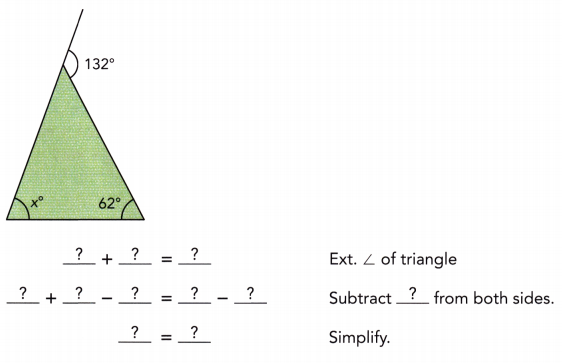
Answer:
x° = 70°
Explanation:
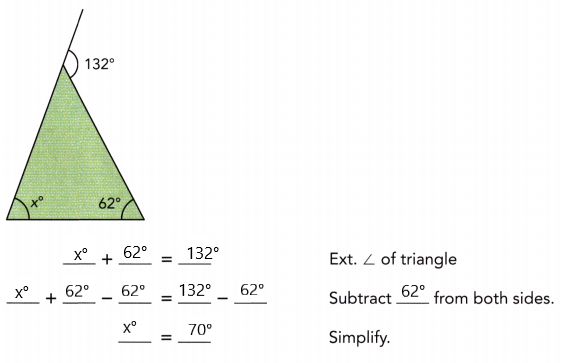
x° + 62° = 132°
x° = 132° – 62°
x° = 70°
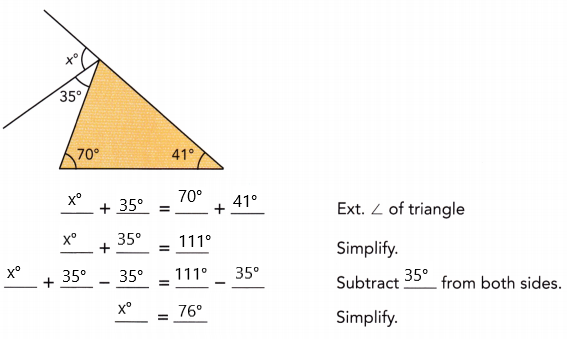
Question 4.
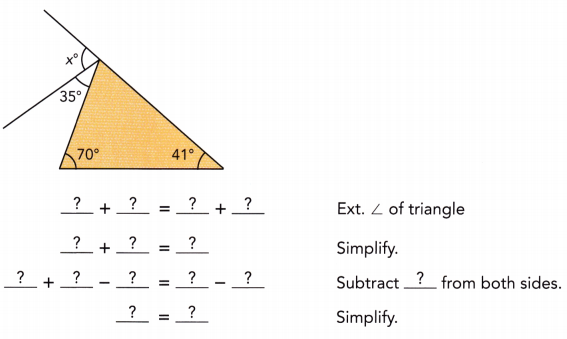
Answer:
x° = 76°
Explanation:
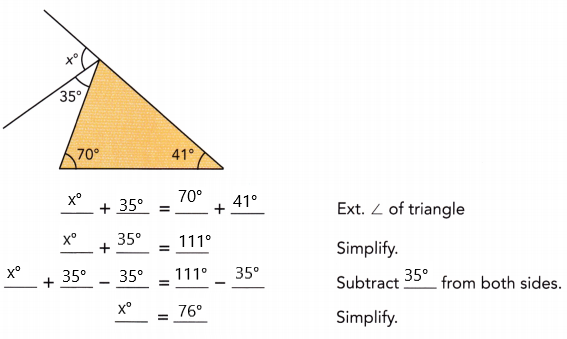
x° + 35°= 70° + 41°
x° + 35° = 111°
x° = 111° – 35°
x° = 76°
Complete.
Question 5.
Triangle ABC is an isosceles triangle. Find the measures of ∠1 and ∠2.
AB = AC
m∠ACB = m∠ABC
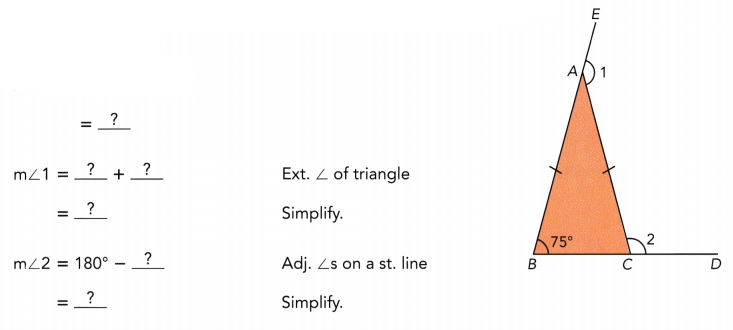
Answer:
∠1 = 255°, ∠2 = 95°
Explanation:
m∠ACB = m∠ABC
∠1 = 75° + 180°
∠1 = 255°
∠2 = 180° – 75°
∠2 = 95°
Question 6.
Triangle EFG is an isosceles triangle and \(\overleftrightarrow{E F}\) is parallel to \(\overleftrightarrow{H I}\). Find the value of x.
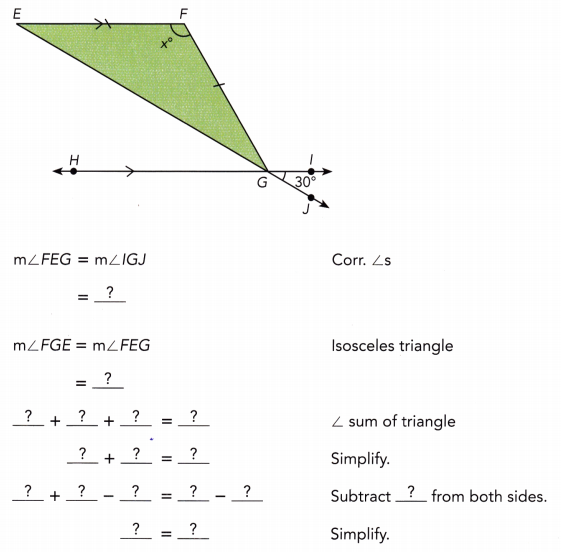
Answer:
x° = 120°
Explanation:
∠FEG = ∠IGJ
= 30°
∠FGE = ∠FEG
= 30°
∠FEG + ∠FGE + ∠EFG = 180°
30° + 30° + x° = 180°
x° + 60° = 180°
x° = 180° -60°
x° = 120°
Math in Focus Course 2B Practice 6.4 Answer Key
Find the value of y.
Question 1.
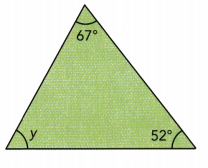
Answer:
y° = 61°
Explanation:
y° + 52° + 67° = 180°
y° + 119° = 180°
y° = 180° -119°
y° = 61°
Question 2.
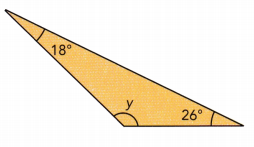
Answer:
y° + 26° + 18° = 180°
y° + 44° = 180°
y° = 180° – 44°
y° = 136°
Question 3.
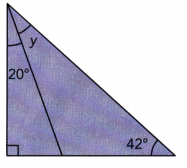
Answer:
20° + y° = 90° + 42°
20° + y° = 132°
y° = 132° -20°
y° = 112°
Question 4.
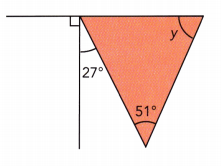
Answer:
90° + 27° + x° = 180°
117° + x° = 180°
x° = 180° -117°
x° = 63°
63° + 51° + y° = 180°
114° + y° = 180°
y° = 180° – 114°
y° = 66°
Question 5.
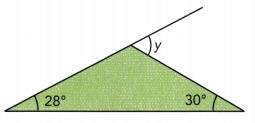
Answer:
y° = 122°
Explanation:
y° + 28° + 30° = 180°
y° + 58° = 180°
y° = 180° – 58°
y° = 122°
Question 6.
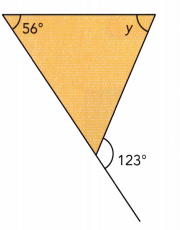
Answer:
x° = 57° , y° = 67°
Explanation:
x° + 123° = 180°
x° = 180° -123°
x° = 57°
56° + 57° + y° = 180°
y° + 113° = 180°
y° = 180° – 113°
y° = 67°
Find m∠1 and m∠2 in each diagram.
Question 7.
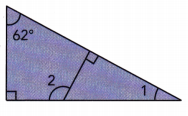
Answer:
62° + 90° + m∠1 = 18o° ∠s sum in triangle:
152° + m∠1 = 180° Simplify:
152° + m∠1 — 152° = 180° — 152° Subtract 152° from both sides:
m∠1 = 28° Simplify:
m∠2 = 90° + m∠1 Exterior ∠ of triangle:
m∠2 = 90° + 28° substitute
m∠2 = 118° simplify
m∠1 = 28°
m∠2 = 118°
Question 8.
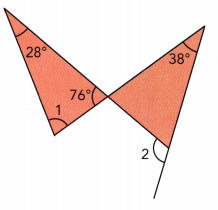
Answer:
∠1 = 76°, ∠2 = 114°
Explanation:
∠1 + 28° + 76° = 180°
∠1 + 104° = 180°
∠1 = 180° – 104°
∠1 = 76°
76° + 38° + x° = 180°
114° + x° = 180°
x° = 180° – 114°
x° = 66°
x° + ∠2 = 180°
66° + ∠2 = 180°
∠2 = 180° – 66°
∠2 = 114°
Question 9.
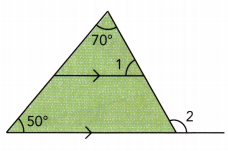
Answer:
50° + 70° + m∠1 = 180° Corresponding ∠s and ∠s sum in triangle:
120° + m∠1 = 180° Simplify:
120° + m∠1 – 120° = 180° – 120° Subtract 120° from both sides:
m∠1 = 60° Simplify:
m∠2 = 50° + 70° Exterior ∠ of triangle:
m∠2 = 120° simplify
m∠1 = 60°
m∠2 = 120°
Question 10.
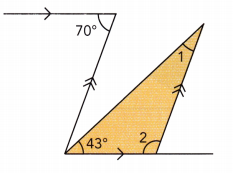
Answer:
70° = 43° + m∠1 Alternate interior ∠s
70° – 43° = 43° + m∠1 – 43° Subtract 43° from both sides:
m∠1 = 27° Simplify:
m∠2 + m∠1 + 43° = 180° ∠s sum of triangle:
m∠2 + 27° + 43° = 180°
m∠2 + 70° = 180° Simplify:
m∠2 + 70° — 70° = 180° — 70° Subtract 70° from both sides:
m∠2 = 110° Simplify:
m∠1 = 27
m∠2 = 110°
Use an equation to find the value of y.
Question 11.
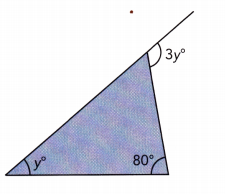
Answer::
3y° = y° + 80° Exterior ∠ of triangle:
3y = y + 80 The equation for y is:
3y – y = y + 80 – y Subtract y from both sides:
2y = 80 Simplify:
\(\frac{2 y}{2}\) = \(\frac{80}{2}\) Divide by 2
y = 40 simplify
3y = y + 80
y = 40
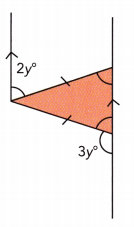
Question 12.
Answer:
Let’s note by x° the measure of the congruent angles of the isosceles triangle
x° = 2y° Alternate interior ∠s
x° + 3y° = 180° Supplementary ∠s:
2y° + 3y° = 180° Substitute:
5y° = 180° Simplify:
\(\frac{5 y^{\circ}}{5}\) = \(\frac{180^{\circ}}{5}\) Divide by 5
y = 36 simplify
2y + 3y = 180
y = 36
Find the value of x and name the type of triangle that is shown.
Question 13.
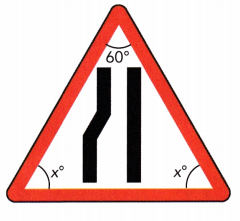
Answer:
x° = 60°, x° = 60°
Explanation:
x° + x° + 60° = 180°
2x° + 60° = 180°
2x° = 180° – 60°
2x° = 120°
x° = 120 ÷ 2
x = 60°
Question 14.
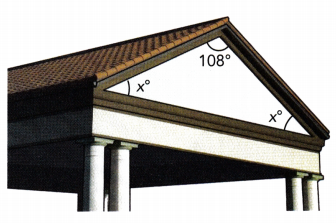
Answer:
x° = 36°, x° = 36°
Explanation:
x°+ x°+ 108° = 180°
2x° + 108° = 180°
2x° = 180° – 108°
2x° = 72°
x° = 72÷2
x° = 36°
Question 15.

Answer:
x° = 8°
Explanation:
We all know that all the angles in a triangle add up to 180 degrees.
In the given figure, each triangle has 3 angles. Thus, we have the sum of three angles as shown:
A° + B° +C° = 180°
62°+ 90°+ x° = 180°
x°+ 172° = 180°
x° = 180° – 172°
x° = 8°
Find the measure of each numbered angle.
Question 16.
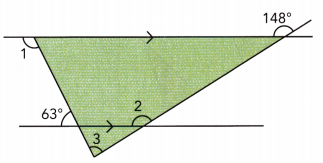
Answer:
m∠2 = 148° Corresponding ∠s:
m∠2 = m∠3 + 63° Vertical ∠s and exterior ∠ of triangle:
148° = m∠3 + 63° Substitute:
148° – 63° = m∠3 + 63° – 63° Subtract 63° from both sides:
m∠3 = 85° Simplify:
m∠1 + 63° = 180° supplementary ∠s
m∠1 + 63° – 63° = 180° – 63° subtract 63° from both sides
m∠1 = 117° simplify
m∠1 = 117°
m∠2 = 148°
m∠3 = 85°
Question 17.
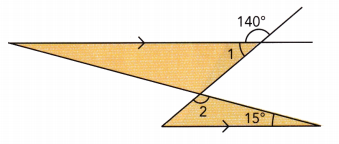
Answer:
m∠1 + 140° = 180° Supplementary ∠s
m∠1 + 140° — 140° = 180° – 140° Subtract 140° from both sides:
m∠1 = 40° Simplify:
m∠2 + 15° + 40° = 180° Alternate interior ∠s and ∠s sum of triangle:
m∠2 + 55° = 180° Simplify:
m∠2 + 55° – 55° = 180° – 55° subtract 55° from both sides
m∠2 = 125° simplify
m∠1 = 40°
m∠2 = 125°
Find the measure of each numbered angle.
Question 18.
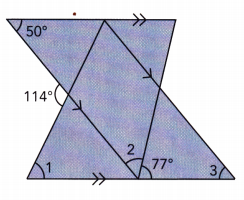
Answer:
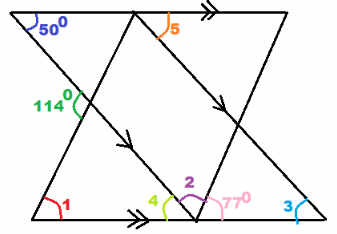
We are given
m∠5 = 50° Corresponding ∠s
m∠3 = m∠5 = 50° Corresponding ∠s
m∠4 = 50° Alternate Interior ∠s
m∠4 + m∠2 + 77° = 180° substitute
m∠2 + 127° = 180° simplify
m∠2 + 127° – 127° = 180° — 127° Subtract 127° from both sides:
m∠2 = 53° Simplify:
114° = m∠1 + m∠4 Exterior ∠ of triangle:
114° = m∠1 + 50° Substitute:
114° – 50° = m∠1 + 50° + 50° Substitute 50° from both sides
m∠1 = 64° simplify
m∠1 = 64°
m∠2 = 53°
m∠3 = 50°
Question 19.
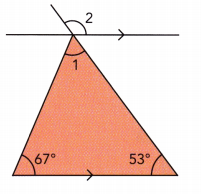
Answer:
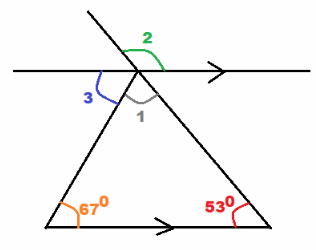
we are given
m∠1 + 67° + 53° = 180° Sum of ∠s in triangle:
m∠1 + 120° = 180° Simplify:
m∠1 + 120° – 120° = 180° — 120° Subtract 120° from both sides:
m∠1 = 60° Simplify:
m∠3 = 67° Alternate interior ∠s
m∠2 = m∠1 + m∠3 vertical ∠s
m∠2 = 60° + 67° substitute
m∠2 = 127° simplify
m∠1 = 60°
m∠2 = 127°
Solve.
Question 20.
\(\overleftrightarrow{\mathrm{BE}}\) is parallel to \(\overleftrightarrow{\mathrm{FH}}\). Find the measure of A
∠CAD in terms of ∠1 and ∠2.
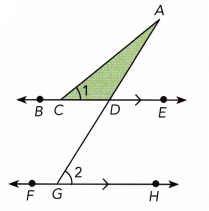
Answer:
m∠ADE = m∠2 Corresponding ∠s:
m∠ADE = m∠CAD + m∠1 Exterior ∠ of triangle:
m∠2 = m∠CAD + m∠1 Substitute:
m∠2 — m∠1 = m∠CAD + m∠1 — m∠1 subtract m∠1 from both sides:
m∠CAD = m∠2 – m∠1 Simplify:
m∠CAD = m∠2 – m∠1
Question 21.
Math Journal
Explain why each of the following statement is true.
a) A triangle cannot have two right angles.
Answer:
m∠A = m∠B = 90° a) Let’s assume that a triangle ABC has two right angles:
m∠A + m∠B + m∠C = 180° Sum of ∠s in triangle:
90° + 90° + m∠C = 180° Substitute:
180° + m∠C = 180° Simplify:
180° + m∠C – 180° = 180° – 180° Subtract 180° from both sides:
m∠C = 0° Simplify:
We got a false statement as the triangle does not exist in this case. Therefore we assumed a wrong statement So a triangle cannot have two right angles.
b) The interior angle measures of an isosceles triangle cannot be 96°, 43°, and 43°.
Answer:
Lets assume that a triangle has the measures of its angles 96°, 43°, 43°
96° + 43° + 43° = 182° We compute the sum of the angles’ measures:
But the sum of a triangle’s angles measures is 180°. We got 182° ≠ 180°, therefore the statement that we assumed is false. So the interior measures of a triangle cannot be 96°, 43°, 43°.
See proofs (sum of the measures of the triangle’s angles)
Question 22.
m∠1 = 2x°, m∠2 = (x – 5)°, and m∠3 = 100°. Use an equation to find the value of x and then find the measures of ∠1 and ∠2.
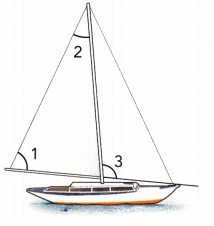
Answer:
∠1 = 80°, ∠2 = 35°
Explanation:
∠1 + ∠3 = 180°
2x° + 100° = 180°
2x° = 180° – 100°
2x° = 80°
x° = 80°÷2
x° = 40°
∠1 = 2×40 = 80°
∠2 = 40 – 5 =35°
Use an equation to find the value of x.
Question 23.
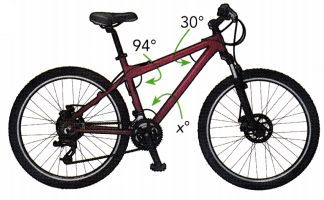
Answer:
x° = 56°
Explanation:
x° + 94°+ 30° = 180°
x° + 124° = 180°
x° = 180° – 124°
x° = 56°
Question 24.
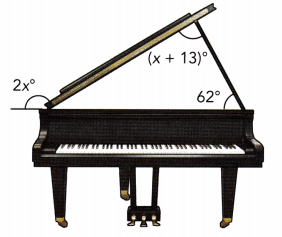
Answer:
x° = 59°, 2x° = 118°
Explanation:
2x° + 62° = 180°
2x° = 180° – 62°
2x° = 118°
x° = 118°÷2
x° = 59°
x + 13 = 59° + 13° = 72°
Use an equation to find the value of x.
Question 25.
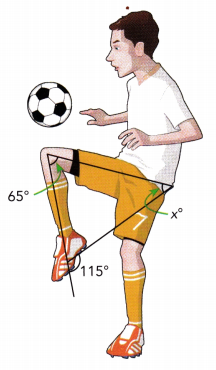
Answer:
x° = 50°, y° = 65°
Explanation:
y° + 115° = 180°
y° = 180° -115°
y° = 65°
65° + 65° + x° = 180°
x° + 130° = 180°
x° = 180° – 130°
x° = 50°
Question 26.
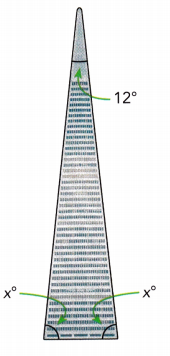
Answer:
x° + x° + 12° = 180°
2x° + 12° = 180°
2x° = 180° – 12°
2x° = 68°
x° = 68 ÷ 2
x° = 34°
Brain@Work
ABCD is a rhombus, and the measure of ∠BCD is 68°. BDE is a triangle where the measure of ∠BED is 36° and the measure of ∠BDE is 73°. Find m∠EBC. Show how you obtain your answer.
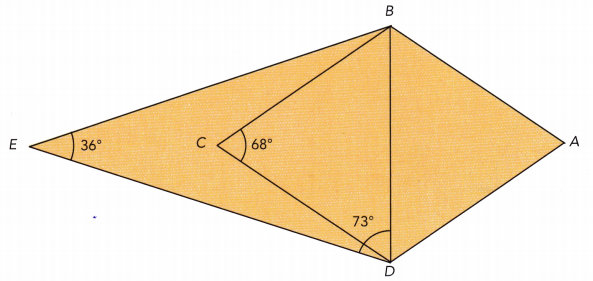
Answer:
m∠EBD + 36° + 73° = 180° Sum of ∠s in triangle:
m∠EBD + 109° = 180° Simplify:
m∠EBD + 109° — 109° = 180° — 109° Subtract 109° from both sides:
m∠EBD = 71° Simplify:
\(\overline{B C}\) = \(\overline{D C}\) ABCD rhombus
m∠CDB = m∠CBD ∆BCD isosceles:
68° + m∠CDB + m∠CBD = 180° Sum of ∠s in triangle:
68° + 2m∠CBD = 180°
68° + 2m∠CBD — 68° = 180° — 68° Subtract 68° from both sides:
2m∠CBD = 112° Simplify:
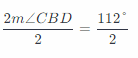
Divide by 2
m∠CBD = 56° Simplify:
m∠EBC = m∠EBD — m∠CBD Substitute:
m∠EBC = 71° — 56°
= 15°