Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 4 Lesson 4.2 Understanding Slope-Intercept Form to finish your assignments.
Math in Focus Grade 8 Course 3 A Chapter 4 Lesson 4.2 Answer Key Understanding Slope-Intercept Form
Technology Activity
Materials
graphing calculator
EXPLORE THE RELATIONSHIP BETWEEN y = mx AND y = mx + b
Work in pairs

Answer:

Math Journal The equation of another line is given by 2y = 5x – 4. It can also be written as y = 2.5x – 2. Predict the y-intercept. Use the graphing calculator to check your prediction. Is your prediction correct?
Answer:
Slope m = 2.5
y-intercept = -2
Math in Focus Grade 8 Chapter 4 Lesson 4.2 Guided Practice Answer Key
Write an equation for each line.
Question 1.
The line passes through the points (![]() ,
, ![]() ) and (
) and (![]() ,
, ![]() ).
).
Slope m = \(\frac{?-?}{?-?}\)
= \(\frac{?}{?}\)
= ![]()
The line intersects the y-axis at the point (![]() ,
, ![]() ).
).
So, the y-intercept is ![]() .
.
So, the equation of the line is ![]() .
.
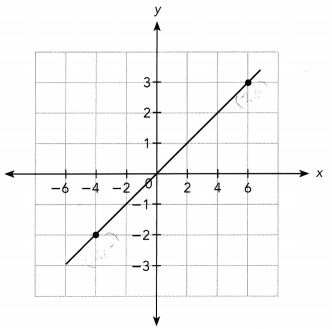
Answer:
The line passes through the points (6, 3) and (-4, -2).
Slope m = \(\frac{6-(-4)}{3-(-2)}\)
= \(\frac{10}{5}\)
= 2
The line passes through the y-axis at the point (0, 0).
Thus m = 2 and y-intercept b is 0.
y = 2x
Question 2.
The line passes through the points (![]() ,
, ![]() ) and (
) and (![]() ,
, ![]() ).
).
Slope m = \(\frac{?-?}{?-?}\)
= \(\frac{?}{?}\)
= ![]()
The line intersects the y-axis at the point (![]() ,
, ![]() ).
).
So, the y-intercept is ![]() .
.
So, the equation of the line is ![]() .
.
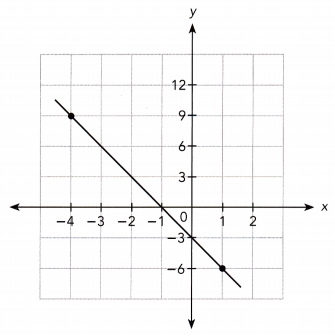
Answer:
The line passes through the points (1, -6) and (-4, 9).
Slope m = \(\frac{9-(-6)}{-4-1}\)
= \(\frac{15}{-5}\)
= -3
The line intersects the y-axis at the point (0, -3).
So, the y-intercept is -3.
So, the equation of the line is y = -3x -3.
Question 3.
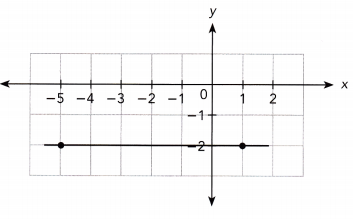
Answer:
The line passes through the points (-5, -2) and (1, -2).
Slope m = \(\frac{-2-(-2)}{1+5}\)
= \(\frac{0}{6}\)
= 0
The line intersects the y-axis at the point (0, -2).
So, the y-intercept is -2.
So, the equation of the line is y = 0x -2.
Question 4.
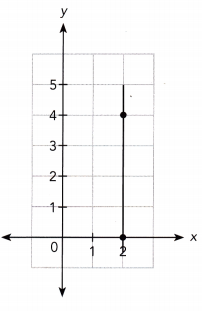
Answer:
The line passes through the points (0, 2) and (2, 4).
Slope m = \(\frac{4-2)}{2-0}\)
= \(\frac{2}{2}\)
= 1
The line intersects the y-axis at the point (0, 0).
So, the y-intercept is 0.
So, the equation of the line is y = -2x + 2
Math in Focus Course 3A Practice 4.2 Answer Key
Identify the y-Intercept. Then calculate the slope using the points indicated.
Question 1.
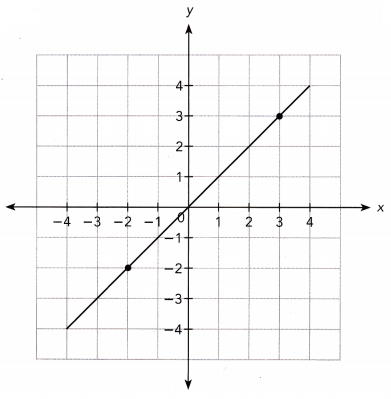
Answer:
The line passes through the points (-2, -2) and (3, 3).
Slope m = \(\frac{3-(-2)}{3-(-2)}\)
= \(\frac{5}{5}\)
= 1
The line intersects the y-axis at the point (0, 0).
So, the y-intercept is 0.
So, the equation of the line is y = x.
Question 2.
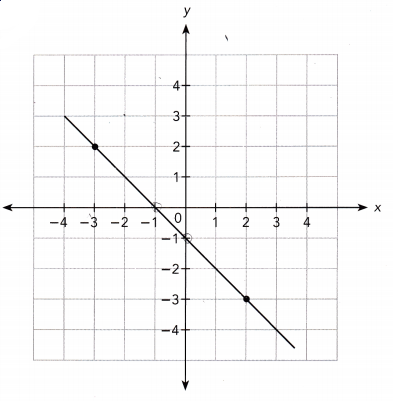
Answer:
The line passes through the points (0, -1) and (2, -3).
Slope m = \(\frac{-3-(-1)}{2-0}\)
= \(\frac{-2}{2}\)
= -1
The line intersects the y-axis at the point (0, -1).
So, the y-intercept is -1.
So, the equation of the line is y = -1x -1.
Question 3.
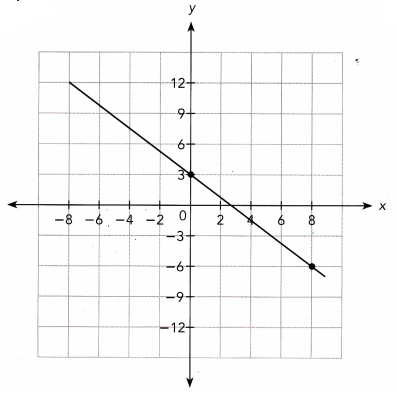
Answer:
The line passes through the points (0, 3) and (8, -6).
Slope m = \(\frac{-6-3}{8-0}\)
= \(\frac{-9}{8}\)
m = \(\frac{-9}{8}\)
The line intersects the y-axis at the point (0, 3).
So, the y-intercept is 3.
Question 4.
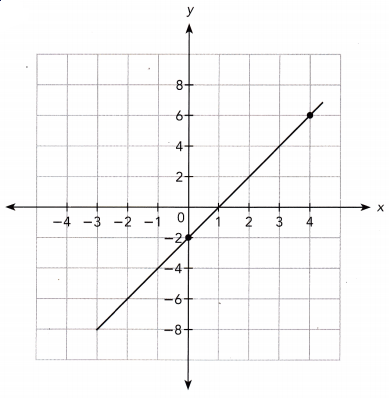
Answer:
The line passes through the points (0, 2) and (4, 6).
Slope m = \(\frac{6-2}{4-0}\)
= \(\frac{4}{4}\)
m = 1
The line intersects the y-axis at the point (0, -2).
So, the y-intercept is -2.
Write an equation in the form y = mx or y = mx + b for each line.
Question 5.
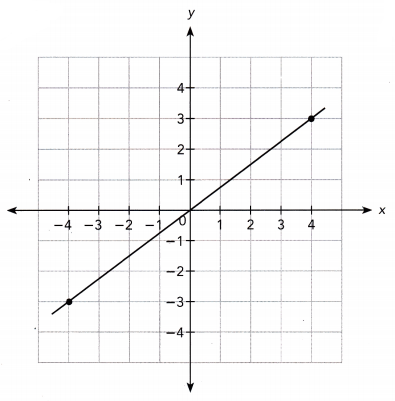
Answer:
The line passes through the points (4, 3) and (-4, -3).
Slope m = \(\frac{-3-3}{-4-4}\)
= \(\frac{-6}{-8}\)
= \(\frac{3}{4}\)
The line intersects the y-axis at the point (0, 0).
So, the y-intercept is 0.
So, the equation of the line is y = \(\frac{3}{4}\)x
Question 6.
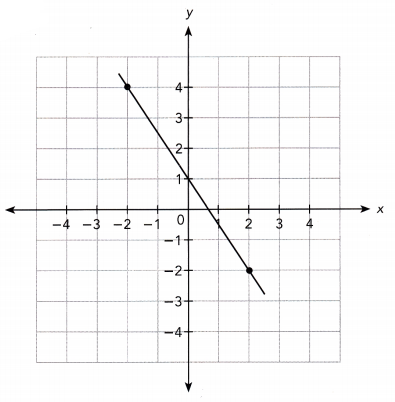
Answer:
The line passes through the points (-2, 4) and (2, -2).
Slope m = \(\frac{-2-4}{2+2}\)
= \(\frac{-6}{4}\)
= \(\frac{-3}{2}\)
The line intersects the y-axis at the point (0, 1).
So, the y-intercept is 1.
So, the equation of the line is y = \(\frac{-3}{2}\)x +1.
Question 7.
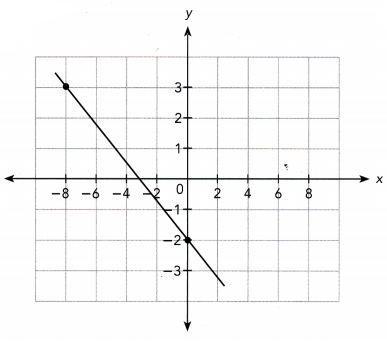
Answer:
The line passes through the points (-8, 3) and (0, -2).
Slope m = \(\frac{-2-3}{0+8}\)
= \(\frac{-5}{8}\)
The line intersects the y-axis at the point (0, -2).
So, the y-intercept is -2.
So, the equation of the line is y = \(\frac{-5}{8}\)x -2.
Question 8.
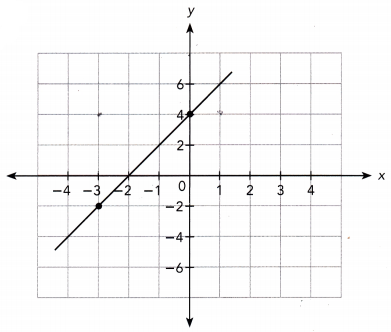
Answer:
The line passes through the points (0, 4) and (-3, -2).
Slope m = \(\frac{-2-4}{-3-0}\)
= \(\frac{-6}{-3}\)
= 2
The line intersects the y-axis at the point (0, 4).
So, the y-intercept is 4.
So, the equation of the line is y = 2x + 4
Graph each line using 1 grid square to represent 1 unit on both axes for the interval from -4 to 4. Then write the equation for each line.
Question 9.
The line passes through the points (-4, 3) and (-4, -2).
Answer:
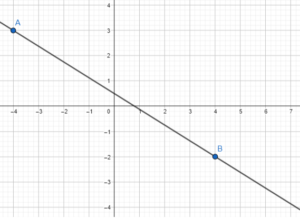
Question 10.
The line passes through the points (-3, 4) and (1, 4).
Answer:
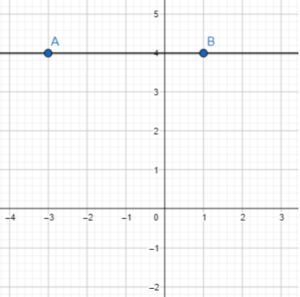
Question 11.
Math Journal Line A passes through the origin and has a negative slope. Line B has a positive y-intercept and a positive slope. Line C has a negative slope and a negative y-intercept. Give a possible equation for each line. Justify your answer.
Answer:
Possible equations: Line A: y = -3x; Line B: y = 5x + 2; Line C: y = -2x – 7.
For line A, the value of m in the equation y = mx + b is negative and the value of b is 0.
For line B, both m and b have positive values. For line C, both m and b have negative values.