Math in Focus Grade 5 Chapter 15 Answer Key Surface Area and Volume

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 15 Surface Area and Volume provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 15 Answer Key Surface Area and Volume

Math Journal

This rectangular container is \(\frac{2}{5}\)-filled with water.
How much more water is needed to increase the height of the water level to 3 centimeters?

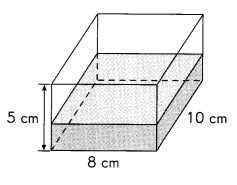
Show two methods of solving this problem. Which method do you prefer? Why?
Answer:
Given rectangular tank has volume 8 cm X 10 cm X 5 cm = 400 cm³,
Method 1:
Knowing the volume of tank and water filled in it
as the rectangular container is \(\frac{2}{5}\)-filled with water.
\(\frac{2}{5}\) X 400 cm³ = 160 cm³, filled with water.
as 1 cubic centimeter is equal to 1 milliliters,

Put on Your Thinking Cap!

Challenging Practice

Question 1.
A rectangular tank is half-filled with water.
Another 650 cubic centimeters of water are needed to make it \(\frac{3}{5}\) full.
How much water will be in the tank when it is \(\frac{3}{5}\) full?
Answer:
3,900 cubic centimeters of water will be in the tank when it is \(\frac{3}{5}\) full,

Explanation:
Given a rectangular tank is half-filled with water.
Another 650 cubic centimeters of water are needed to make it \(\frac{3}{5}\) full.
Let x cubic centimeters of water so \(\frac{1}{2}\)x + \(\frac{3}{5}\)x = 650 cm³ + x,
\(\frac{5x + 6x}{10}\) = 650 cm³ + x,
\(\frac{11x}{10}\) = 650 cm³ + x,
11 x = 10 X (650 cm³ + x),
11 x =  6500 cm³ + 10 x,
11x – 10 x = 6,500 cm³,
x = 6,500 cm³,
So, water will be in the tank when it is \(\frac{3}{5}\) full is
\(\frac{3}{5}\) x 6,500 cm³ = \(\frac{3 X 6,500}{5}\) cm³,
\(\frac{19,500}{5}\) cm³ = 3,900 cm³,
therefore 3,900 cubic centimeters of water will be in the tank when it is \(\frac{3}{5}\) full.

Question 2.
A cube has a surface area of 21 6 square centimeters.
A second cube has edges that are 3 times as long.
How much greater is the surface area of the second cube than the first cube?
Answer:
1,728 cm² greater is the surface area of the second cube than the first cube,

Explanation:
Given a cube has a surface area of 216 square centimeters as
surface area of cube is 6 X a²= 216 cm²,
a² = 36 cm² = 6 cm X 6 cm,
edge a    = 6 cm,
A second cube has edges that are 3 times long as
6 cm X 3 = 18 cm, Surface area of second cube is 6 x (18)² =
6 X 18 cm X 18 cm = 1,944 cm², Now compairing much greater is the
surface area of the second cube than the first cube is 1,944 cm² – 216 cm² = 1,728 cm².

Put on Your Thinking Cap!

Problem Solving

A prism has a square base whose edges each measure 5 centimeters.
The ratio of its height to its width is 4 : 1.
Find the volume of the rectangular prism in cubic centimeters.

Answer:
Given a prism has a square base whose edge each measure 5 centimeters.
height = 4 cm
width = 1 cm
Volume of the rectangular prism = 2l × 2w × 2h
V = 2 × 5 × 2 × 1 × 2 × 4
V = 80 cubic centimeters