This handy Math in Focus Grade 7 Workbook Answer Key Chapter 9 Review Test detailed solutions for the textbook questions.
Math in Focus Grade 7 Course 2 B Chapter 9 Review Test Answer Key
Concepts and Skills
Find the range, the three quartiles, and the interquartile range.
Question 1.
2, 4, 1, 7, 3, 3, 9, 10, 1, 0, 6, 8, 5, 5, 9
Answer:
The range in statistics for a given data set is the difference between the highest and lowest values.
Range=maximum observation-minimum observation
how to find range:
To find the range in statistics, we need to arrange the given values or set of data or set of observations in ascending order. That means, firstly write the observations from the lowest to the highest value. Now, we need to use the formula to find the range of observations.
Ascending order:
0, 1, 1, 2, 3, 3, 4, 5, 5, 6, 7, 8, 9, 9, 10
Maximum value=10
Minimum value=0
range=10-0
range=10
Quartiles:
Quartiles mark each 25% of a set of data:
1. The first quartile Q1 is the 25th percentile
2. The second quartile Q2 is the 50th percentile
3. The third quartile Q3 is the 75th percentile
The second quartile Q2 is easy to find. It is the median of any data set and it divides an ordered data set into upper and lower halves.
Data set: 0, 1, 1, 2, 3, 3, 4, 5, 5, 6, 7, 8, 9, 9, 10
Q2=5
The first quartile Q1 is the median of the lower half not including the value of Q2. The third quartile Q3 is the median of the upper half not including the value of Q2.
n=15 (odd)
0, 1, 1, 2, 3, 3, 4
If the size of the data set is odd, do not include the median when finding the first and third quartiles.
Q1=2
Q3 data set: 5, 6, 7, 8, 9, 9, 10
Q3=8
Interquartile range=Q3-Q1
Interquartile range=8-2
Interquartile range=6
Question 2.
34, 66, 90, 25, 46, 81, 40, 67, 95, 104, 36, 49
Answer:
The range in statistics for a given data set is the difference between the highest and lowest values.
Range=maximum observation-minimum observation
how to find range:
To find the range in statistics, we need to arrange the given values or set of data or set of observations in ascending order. That means, firstly write the observations from the lowest to the highest value. Now, we need to use the formula to find the range of observations.
Ascending order:
25, 34, 36, 40, 46, 49, 66, 67, 81, 90, 95, 104
Maximum value=104
Minimum value=25
Range=104-25
Range=79
Quartiles:
Quartiles mark each 25% of a set of data:
1. The first quartile Q1 is the 25th percentile
2. The second quartile Q2 is the 50th percentile
3. The third quartile Q3 is the 75th percentile
The second quartile Q2 is easy to find. It is the median of any data set and it divides an ordered data set into upper and lower halves.
Data set=25, 34, 36, 40, 46, 49, 66, 67, 81, 90, 95, 104
Q2=49+66/2
Q2=115/2
Q2=57.5
The first quartile Q1 is the median of the lower half not including the value of Q2. The third quartile Q3 is the median of the upper half not including the value of Q2.
Q1 data set: 25, 34, 36, 40, 46, 49
Q1=36+40/2
Q1=76/2
Q1=38
Q1 is the median of the lower half of the data.
Q3 data set: 66, 67, 81, 90, 95, 104
Q3=81+90/2
Q3=171/2
Q3=85.5
Interquartile range=Q3-Q1
Interquartile range=85.5-38
Interquartile range=47.5
Question 3.
1.23, 1.45, 1.09, 1.78, 1.55, 1.67, 1.37, 1.05, 1.23, 1.11
Answer:
The range in statistics for a given data set is the difference between the highest and lowest values.
Range=maximum observation-minimum observation
how to find range:
To find the range in statistics, we need to arrange the given values or set of data or set of observations in ascending order. That means, firstly write the observations from the lowest to the highest value. Now, we need to use the formula to find the range of observations.
Ascending order:
1.05, 1.09, 1.11, 1.23, 1.23, 1.37, 1.45, 1.55, 1.67, 1.78
Maximum value=1.78
Minimum value=1.05
Range=1.78-1.05
Range=0.73
Quartiles:
Quartiles mark each 25% of a set of data:
1. The first quartile Q1 is the 25th percentile
2. The second quartile Q2 is the 50th percentile
3. The third quartile Q3 is the 75th percentile
The second quartile Q2 is easy to find. It is the median of any data set and it divides an ordered data set into upper and lower halves.
Data set: 1.05, 1.09, 1.11, 1.23, 1.23, 1.37, 1.45, 1.55, 1.67, 1.78
Q2=1.23+1.37/2
Q2=2.6/2
Q2=1.3
The first quartile Q1 is the median of the lower half not including the value of Q2. The third quartile Q3 is the median of the upper half not including the value of Q2.
Q1 data set: 1.05, 1.09, 1.11, 1.23, 1.23
Q1=1.11
Q3 data set: 1.37, 1.45, 1.55, 1.67, 1.78
Q3=1.55
Interquartile range=Q3-Q1
Interquartile range=1.55-1.11
Interquartile range=0.44
Question 4.
162.5, 248.6, 130.7, 344.9, 322.0, 234.2, 150.8, 304.7, 326.4
Answer:
The range in statistics for a given data set is the difference between the highest and lowest values.
Range=maximum observation-minimum observation
how to find range:
To find the range in statistics, we need to arrange the given values or set of data or set of observations in ascending order. That means, firstly write the observations from the lowest to the highest value. Now, we need to use the formula to find the range of observations.
Ascending order:
130.7, 150.8, 162.5, 234.2, 248.6, 304.7, 322.0, 326.4, 344.9
Maximum value=344.9
Minimum value=130.7
Range=344.9-130.7
Range=214.2
Quartiles:
Quartiles mark each 25% of a set of data:
1. The first quartile Q1 is the 25th percentile
2. The second quartile Q2 is the 50th percentile
3. The third quartile Q3 is the 75th percentile
The second quartile Q2 is easy to find. It is the median of any data set and it divides an ordered data set into upper and lower halves.
Data set: 130.7, 150.8, 162.5, 234.2, 248.6, 304.7, 322.0, 326.4, 344.9
Q2= 248.6
n=9 (odd)
If the size of the data set is odd, do not include the median when finding the first and third quartiles.
The first quartile Q1 is the median of the lower half not including the value of Q2. The third quartile Q3 is the median of the upper half not including the value of Q2.
Q1 data set: 130.7, 150.8, 162.5, 234.2
Q1=150.8+162.5/2
Q1=313.3/2
Q1=156.65
Q3 data set: 304.7, 322.0, 326.4, 344.9
Q3=322.0+326.4/2
Q3=648.4/2
Q3=324.2
Interquartile range=Q3-Q1
Interquartile range=324.2-156.65
Interquartile range=167.55
Use the information below to answer the following.
Tara tossed two number dice 24 times. She found the sum of the values for each throw and displayed the sums in a dot plot.
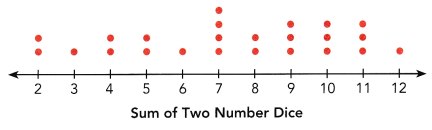
Question 5.
Find the range of the data.
Answer:
The range in statistics for a given data set is the difference between the highest and lowest values.
Range=maximum observation-minimum observation
how to find range:
To find the range in statistics, we need to arrange the given values or set of data or set of observations in ascending order. That means, firstly write the observations from the lowest to the highest value. Now, we need to use the formula to find the range of observations.
According to the dot plot the data set will be:
2, 2, 3, 4, 4, 5, 5, 6, 7, 7, 7, 7, 8, 8, 9, 9, 9, 10, 10, 10, 11, 11, 11, 12.
maximum value=12
minimum value=2
Range=12-2
Range=10
Question 6.
Find the 3 quartiles of the data.
Answer:
Quartiles:
Quartiles mark each 25% of a set of data:
1. The first quartile Q1 is the 25th percentile
2. The second quartile Q2 is the 50th percentile
3. The third quartile Q3 is the 75th percentile
The second quartile Q2 is easy to find. It is the median of any data set and it divides an ordered data set into upper and lower halves.
The given data set: 2, 2, 3, 4, 4, 5, 5, 6, 7, 7, 7, 7, 8, 8, 9, 9, 9, 10, 10, 10, 11, 11, 11, 12.
Q2=7+8/2
Q2=15/2
Q2=7.5
The first quartile Q1 is the median of the lower half not including the value of Q2. The third quartile Q3 is the median of the upper half not including the value of Q2.
Q1 data set: 2, 2, 3, 4, 4, 5, 5, 6, 7, 7, 7, 7
Q1=5+5/2
Q1=10/2
Q1=5
Q1 is the median of the lower half of the data.
Q3 data set: 8, 8, 9, 9, 9, 10, 10, 10, 11, 11, 11, 12
Q3=10+10/2
Q3=20/2
Q3=10
Q3 is the median of the upper half of the data.
Question 7.
Find the interquartile range.
Answer:
The interquartile range defines the difference between the third and the first quartile. Quartiles are the partitioned values that divide the whole series into 4 equal parts. So, there are 3 quartiles. First Quartile is denoted by Q1 known as the lower quartile, the second Quartile is denoted by Q2 and the third Quartile is denoted by Q3 known as the upper quartile. Therefore, the interquartile range is equal to the upper quartile minus the lower quartile.
The difference between the upper and lower quartile is known as the interquartile range. The formula for the interquartile range is given below
Interquartile range = Upper Quartile – Lower Quartile = Q3 – Q1
where Q1 is the first quartile and Q3 is the third quartile of the series.
Q1=5; Q3=10
Interquartile range=Q3-Q1
Interquartile range=10-5
Interquartile range=5
Solve. Show your work.
Question 8.
The map shows the maximum temperature, in degrees Fahrenheit, recorded in 20 cities across the United States in a certain year. Display the data in a stem-and-leaf plot.
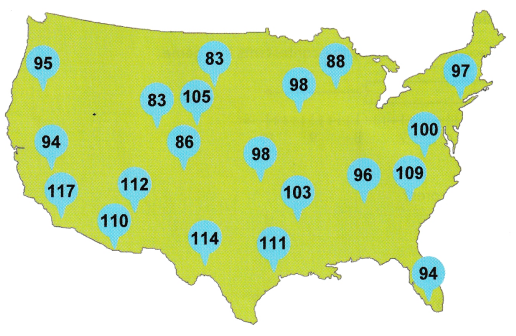
Answer:
The Stem and Leaf plot is a way of organizing data into a form that makes it easy to see the frequency of different values. In other words, we can say that a Stem and Leaf Plot is a table in which each data value is split into a “stem” and a “leaf.” The “stem” is the left-hand column that has the tens of digits. The “leaves” are listed in the right-hand column, showing all the ones digit for each of the tens, the twenties, thirties, and forties. Remember that Stem and Leaf plots are a pictorial representation of grouped data, but they can also be called a modal representation. Because, by quick visual inspection at the Stem and Leaf plot, we can determine the mode.
Steps for making:
1. First, determine the smallest and largest number in the data.
2. Identify the stems.
3. Draw a with two columns and name them as “Stem” and “Leaf”.
4. Fill in the leaf data.
5. Remember, a Stem and Leaf plot can have multiple sets of leaves.
The given data:95, 94, 117, 110, 112, 86, 83, 105, 83, 114, 111, 103, 98, 98, 88, 96, 109, 100, 97, 94
Ascending order:83, 83, 86, 88, 94, 94, 95, 96, 97, 98, 98, 100, 103, 105, 109, 110, 111, 112, 114, 117

Question 9.
The table shows the weights of Labrador dogs, in pounds.
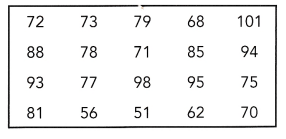
a) Draw a stem-and-leaf plot for the data.
Answer:
The given data: 72, 73, 79, 68, 101, 88, 78, 71, 85, 94, 93, 77, 98, 95, 75, 81, 56, 51, 62, 70
The Stem and Leaf plot is a way of organizing data into a form that makes it easy to see the frequency of different values. In other words, we can say that a Stem and Leaf Plot is a table in which each data value is split into a “stem” and a “leaf.” The “stem” is the left-hand column that has the tens of digits. The “leaves” are listed in the right-hand column, showing all the ones digit for each of the tens, the twenties, thirties, and forties. Remember that Stem and Leaf plots are a pictorial representation of grouped data, but they can also be called a modal representation. Because, by quick visual inspection at the Stem and Leaf plot, we can determine the mode.
Steps for making:
1. First, determine the smallest and largest number in the data.
2. Identify the stems.
3. Draw a with two columns and name them as “Stem” and “Leaf”.
4. Fill in the leaf data.
5. Remember, a Stem and Leaf plot can have multiple sets of leaves.
Ascending order: 51, 56, 62, 68, 70, 71, 72, 73, 75, 77, 78, 79, 81, 85, 88, 93, 94, 95, 98, 101

5|1 represents 51 pounds.
b) How many Labrador dogs are there?
Answer:
The given data: 72, 73, 79, 68, 101, 88, 78, 71, 85, 94, 93, 77, 98, 95, 75, 81, 56, 51, 62, 70
the number of given data is equal to number of Labrador dogs.
Now count the numbers present in the sata set.
There are 20 Labrador dogs.
c) What is the range?
Answer:
The range in statistics for a given data set is the difference between the highest and lowest values.
Range=maximum observation-minimum observation
how to find range:
To find the range in statistics, we need to arrange the given values or set of data or set of observations in ascending order. That means, firstly write the observations from the lowest to the highest value. Now, we need to use the formula to find the range of observations.
The given data: 72, 73, 79, 68, 101, 88, 78, 71, 85, 94, 93, 77, 98, 95, 75, 81, 56, 51, 62, 70
Ascending order: 51, 56, 62, 68, 70, 71, 72, 73, 75, 77, 78, 79, 81, 85, 88, 93, 94, 95, 98, 101
Maximum value=101
Minimum value=51
range=101-51
range=50
d) What is the mode of the data?
Answer:
The mode is the observation’s value, which occurs most frequently, i.e., an observation with the maximum frequency is called the mode. A data set can have more than one mode, which means more than one observation has the same maximum frequency.
The given data: 72, 73, 79, 68, 101, 88, 78, 71, 85, 94, 93, 77, 98, 95, 75, 81, 56, 51, 62, 70
Ascending order: 51, 56, 62, 68, 70, 71, 72, 73, 75, 77, 78, 79, 81, 85, 88, 93, 94, 95, 98, 101
Therefore, there is no modal weight. No number doesn’t occur more times.
e) What is the median weight?
Answer:
The median of a set of data is the middlemost number or centre value in the set. The median is also the number that is halfway into the set. To find the median, the data should be arranged, first, in order of least to greatest or greatest to the least value. A median is a number that is separated by the higher half of a data sample, a population or a probability distribution, from the lower half. The median is different for different types of distribution.
Formula:
The formula to calculate the median of the finite number of data set is given here. The median formula is different for even and odd numbers of observations. Therefore, it is necessary to recognise first if we have an odd number of values or an even number of values in a given data set.
The formula to calculate the median of the data set is given as follow.
An odd number of observations:
If the total number of observation given is odd, then the formula to calculate the median is:
Median = {(n+1)/2}thterm; where n is the number of observations
Even number of observations:
If the total number of observations is even, then the median formula is:
Median = [(n/2)th term + {(n/2)+1}th]/2; where n is the number of observations
The given data: 72, 73, 79, 68, 101, 88, 78, 71, 85, 94, 93, 77, 98, 95, 75, 81, 56, 51, 62, 70
Ascending order: 51, 56, 62, 68, 70, 71, 72, 73, 75, 77, 78, 79, 81, 85, 88, 93, 94, 95, 98, 101
Median=77+78/2
Median=155/2
Median=77.5 lb
Find the mean absolute deviation.
Question 10.
57, 60, 31, 30, 26, 46, 52, 40, 35, 60
Answer:
To understand Mean Absolute Deviation, let us split both the words and try to figure out their meaning. ‘Mean’ refers to the average of the observations and deviation implies departure or variation from a preset standard. When put together, we can define mean deviation as the mean distance of each observation from the mean of the data.
formula:
The ratio of the sum of all absolute values of deviation from central measure to the total number of observations.
M.A. D = (Σ Absolute Values of Deviation from Central Measure) / (Total Number of Observations)
Calculate MAD:
Steps to find the mean deviation from mean:
(i)Find the mean of the given observations.
(ii)Calculate the difference between each observation and the calculated mean
(iii)Evaluate the mean of the differences obtained in the second step.
This gives you the mean deviation from the mean.
The given data set: 57, 60, 31, 30, 26, 46, 52, 40, 35, 60
First, we have to calculate the mean:
Mean= sum of observations/total number of observations
Mean=57+60+31+30+26+46+52+40+35+60/10
Mean=437/10
mean=43.7
Now calculate the difference between each observation and the calculated mean
|57-43.7|=13.3
|60-43.7|=16.3
|31-43.7|=12.7
|30-43.7|=13.7
|26-43.7|=17.7
|46-43.7|=2.3
|52-43.7|=8.3
|40-43.7|=3.7
|35-43.7|=8.7
|60-43.7|=16.3
Now calculate the mean for obtained differences
MAD=13.3+16.3+12.7+13.7+17.7+2.3+8.3+3.7+8.7+16.3/10
MAD=113/13
MAD=11.3
Question 11.
1.46, 2.03, 3.12, 2.55, 4.25, 1.80, 4.08, 2.87
Answer:
To understand Mean Absolute Deviation, let us split both the words and try to figure out their meaning. ‘Mean’ refers to the average of the observations and deviation implies departure or variation from a preset standard. When put together, we can define mean deviation as the mean distance of each observation from the mean of the data.
formula:
The ratio of the sum of all absolute values of deviation from central measure to the total number of observations.
M.A. D = (Σ Absolute Values of Deviation from Central Measure) / (Total Number of Observations)
Calculate MAD:
Steps to find the mean deviation from mean:
(i)Find the mean of the given observations.
(ii)Calculate the difference between each observation and the calculated mean
(iii)Evaluate the mean of the differences obtained in the second step.
This gives you the mean deviation from the mean.
The given data set: 1.46, 2.03, 3.12, 2.55, 4.25, 1.80, 4.08, 2.87
First, we have to calculate the mean:
Mean= sum of observations/total number of observations
Mean=1.46+2.03+3.12+2.55+4.25+1.80+4.08+2.87/8
Mean=22.16/8
mean=2.77
Now calculate the difference between each observation and the calculated mean
|1.46-2.77|=1.31
|2.03-2.77|=0.74
|3.12-2.77|=0.35
|2.55-2.77|=0.22
|4.25-2.77|=1.48
|1.80-2.77|=0.97
|4.08-2.77|=1.31
|2.87-2.77|=0.1
Now calculate the mean for obtained differences
MAD=1.31+0.74+0.35+0.22+1.48+0.97+1.31+0.1/8
MAD=6.48/8
MAD=0.81
Refer to the box plot to answer the following.
The box plot summarizes the heights of bean sprouts, in centimeters.

Question 12.
Find the lower quartile, the median, and the upper quartile.
Answer:
Quartiles:
Quartiles mark each 25% of a set of data:
1. The first quartile Q1 is the 25th percentile
2. The second quartile Q2 is the 50th percentile
3. The third quartile Q3 is the 75th percentile
Quartiles divide the entire set into four equal parts. So, there are three quartiles, first, second and third represented by Q1, Q2 and Q3, respectively. Q2 is nothing but the median, since it indicates the position of the item in the list and thus, is a positional average. To find quartiles of a group of data, we have to arrange the data in ascending order.
Suppose, Q3 is the upper quartile is the median of the upper half of the data set. Whereas, Q1 is the lower quartile and median of the lower half of the data set. Q2 is the median.
The box plot summarizes five points. They are:
Lowest value; Q1 (lower quartile); Q2 (median); Q3 (upper quartile); highest value.
Now observe the box plot and record the corresponding values.
Lowest value=3.9
Q1 (lower quartile)=4.3;
Q2 (median)=4.4;
Q3 (upper quartile)=4.7
Highest value=5.1
Question 13.
Calculate the range and the interquartile range.
Answer:
The range in statistics for a given data set is the difference between the highest and lowest values.
Range=maximum observation-minimum observation
how to find range:
To find the range in statistics, we need to arrange the given values or set of data or set of observations in ascending order. That means, firstly write the observations from the lowest to the highest value. Now, we need to use the formula to find the range of observations.
the data set: 3.9, 4.0, 4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8, 4.9, 5.0, 5.1
Maximum value=5.1
Minimum value=3.9
range=5.1-3.9
range=1.2 cms
Interquartile range:
The interquartile range defines the difference between the third and the first quartile. Quartiles are the partitioned values that divide the whole series into 4 equal parts. So, there are 3 quartiles. First Quartile is denoted by Q1 known as the lower quartile, the second Quartile is denoted by Q2 and the third Quartile is denoted by Q3 known as the upper quartile. Therefore, the interquartile range is equal to the upper quartile minus the lower quartile.
The difference between the upper and lower quartile is known as the interquartile range. The formula for the interquartile range is given below
Interquartile range = Upper Quartile – Lower Quartile = Q3 – Q1
where Q1 is the first quartile and Q3 is the third quartile of the series.
We know Q3=4.7; Q1=4.3 from this we can calculate IQR
IQR=Q3-Q1
IQR=4.7-4.3
IQR=0.4 cms
Question 14.
Math Journal Interpret what the range means in this context.
Answer:
The range in statistics for a given data set is the difference between the highest and lowest values.
Range=maximum observation-minimum observation
how to find range:
To find the range in statistics, we need to arrange the given values or set of data or set of observations in ascending order. That means, firstly write the observations from the lowest to the highest value. Now, we need to use the formula to find the range of observations.
the data set: 3.9, 4.0, 4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8, 4.9, 5.0, 5.1
Maximum value=5.1
Minimum value=3.9
range=5.1-3.9
range=1.2 cms
Question 15.
Math Journal Interpret what the interquartile range means.
Answer:
The interquartile range defines the difference between the third and the first quartile. Quartiles are the partitioned values that divide the whole series into 4 equal parts. So, there are 3 quartiles. First Quartile is denoted by Q1 known as the lower quartile, the second Quartile is denoted by Q2 and the third Quartile is denoted by Q3 known as the upper quartile. Therefore, the interquartile range is equal to the upper quartile minus the lower quartile.
The difference between the upper and lower quartile is known as the interquartile range. The formula for the interquartile range is given below
Interquartile range = Upper Quartile – Lower Quartile = Q3 – Q1
where Q1 is the first quartile and Q3 is the third quartile of the series.
We know Q3=4.7; Q1=4.3 from this we can calculate IQR
IQR=Q3-Q1
IQR=4.7-4.3
IQR=0.4 cms
Therefore, the spread of the middle 50% heights of the bean sprouts is 0.4 cms.
Use the box plot to answer the following.
The box plot below summarizes the scores obtained by the contestants in a game.

Question 16.
What are the greatest and the least scores?
Answer:
Quartiles:
Quartiles mark each 25% of a set of data:
1. The first quartile Q1 is the 25th percentile
2. The second quartile Q2 is the 50th percentile
3. The third quartile Q3 is the 75th percentile
Quartiles divide the entire set into four equal parts. So, there are three quartiles, first, second and third represented by Q1, Q2 and Q3, respectively. Q2 is nothing but the median, since it indicates the position of the item in the list and thus, is a positional average. To find quartiles of a group of data, we have to arrange the data in ascending order.
Suppose, Q3 is the upper quartile is the median of the upper half of the data set. Whereas, Q1 is the lower quartile and median of the lower half of the data set. Q2 is the median.
The box plot summarizes five points. They are:
Lowest value; Q1 (lower quartile); Q2 (median); Q3 (upper quartile); highest value.
Now observe the box plot and record the corresponding values.
Here asked only greatest and least scores:
Greatest score=10
least score=0
Question 17.
Find the first, second, and third quartiles.
Answer:
Quartiles:
Quartiles mark each 25% of a set of data:
1. The first quartile Q1 is the 25th percentile
2. The second quartile Q2 is the 50th percentile
3. The third quartile Q3 is the 75th percentile
Quartiles divide the entire set into four equal parts. So, there are three quartiles, first, second and third represented by Q1, Q2 and Q3, respectively. Q2 is nothing but the median, since it indicates the position of the item in the list and thus, is a positional average. To find quartiles of a group of data, we have to arrange the data in ascending order.
Suppose, Q3 is the upper quartile is the median of the upper half of the data set. Whereas, Q1 is the lower quartile and median of the lower half of the data set. Q2 is the median.
The box plot summarizes five points. They are:
Lowest value; Q1 (lower quartile); Q2 (median); Q3 (upper quartile); highest value.
Now observe the box plot and record the corresponding values.
Q1 (lower quartile)=4;
Q2 (median)=5.4;
Q3 (upper quartile)=7.8
Question 18.
If there are 160 contestants, how many scored 4 or more points?
Answer:
The number of contenstants=160
The number of members scored 4 or more=X
The maximum score is 10
X=160/10
X=16
Therefore, 16 members scored 4 or more points.
Problem Solving
Use the statistics given ¡n the table to answer questions 19 to 21.
In a population of 200 students taking a science test, the following statistics for the test scores were compiled.

Question 19.
Math Journal By comparing the mean, the median, and the mode, what can you infer about the distribution of the test scores?
Answer:
The middle 50% of the science scores are moderately spread out from 38 to 76 and the mean is quite close to the median, making the distribution fairly symmetrical about the mean.
Question 20.
Math Journal By analyzing the statistics in the table, what can you infer about the variation of the scores?
Answer:
Inbetween the lowest and highest score the scores varied from one to one. The mean is quite close to the median.
Coming to quartiles there is a lot of variation from lower quartile to upper quartile.
Question 21.
Estimate the number of students who scored 76 or less.
Answer: 150 students.
The total number of students=200
76 or less means it can be 76 or 75, 74… up to 26 because it is the least number.
Suppose take 75% of 200
75*200/100
=150
Therefore, 150 students scored 76 or less.
Use the data in the table to answer questions 22 to 27.
The table summarizes the monthly sales figures, in thousands of dollars, for the women’s and men’s clothing departments at a store. For instance, sales in the women’s department in January were $10,000.

Question 22.
Calculate the 5-point summary for each of the two departments.
Answer:
Quartiles mark each 25% of a set of data:
1. The first quartile Q1 is the 25th percentile
2. The second quartile Q2 is the 50th percentile
3. The third quartile Q3 is the 75th percentile
Quartiles divide the entire set into four equal parts. So, there are three quartiles, first, second and third represented by Q1, Q2 and Q3, respectively. Q2 is nothing but the median, since it indicates the position of the item in the list and thus, is a positional average. To find quartiles of a group of data, we have to arrange the data in ascending order.
Suppose, Q3 is the upper quartile is the median of the upper half of the data set. Whereas, Q1 is the lower quartile and median of the lower half of the data set. Q2 is the median.
The box plot summarizes five points. They are:
Lowest value; Q1 (lower quartile); Q2 (median); Q3 (upper quartile); highest value.
Now observe the box plot and record the corresponding values.
The data set for women: 10, 15, 8, 12, 28, 34, 36, 18, 14, 16, 27, 40
The data set for men: 8, 10, 11, 15, 20, 30, 24, 14, 10, 9, 17, 28
Ascending order for women: 8, 10, 12, 14, 15, 16, 18, 27, 28, 34, 36, 40
Least point=8
Highest point=40
Q2=16+18/2
Q2=34/2
Q2=17
The first quartile Q1 is the median of the lower half not including the value of Q2. The third quartile Q3 is the median of the upper half not including the value of Q2.
Q1 data set: 8, 10, 12, 14, 15, 16
Q1=12+14/2
Q1=26/2
Q1=13
Q1 is the median of the lower half of the data.
Q3 data set: 18, 27, 28, 34, 36, 40
Q3=28+34/2
Q3=62/2
Q3=31
Q3 is the median of the upper half of the data.
Men’s department:
The data set for men: 8, 10, 11, 15, 20, 30, 24, 14, 10, 9, 17, 28
Ascending order: 8, 9, 10, 10, 11, 14, 15, 17, 20, 24, 28, 30
Lowest value=8
Highest value=30
Q2=14+15/2
Q2=29/2
Q2=14.5
Q1 data set: 8, 9, 10, 10, 11, 14
Q1=10+10/2
Q1=20/2
Q1=10
Q1 is the median of the lower half of the data.
Q3 data set: 15, 17, 20, 24, 28, 30
Q3=20+24/2
Q3=44/2
Q3=22
Q3 is the median of the upper half of the data.
Question 23.
Using the same scale, draw 2 box plots, one for each department.
Answer:
When we display the data distribution in a standardized way using 5 summary – minimum, Q1 (First Quartile), median, Q3(third Quartile), and maximum, it is called a Box plot. It is also termed a box and whisker plot.
A box plot is a chart that shows data from a five-number summary including one of the measures of central tendency. It does not show the distribution in particular as much as a stem and leaf plot or histogram does. But it is primarily used to indicate a distribution is skewed or not and if there are potential unusual observations (also called outliers) present in the data set. Boxplots are also very beneficial when large numbers of data sets are involved or compared.

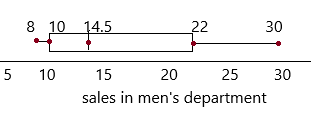
Question 24.
Math Journal By comparing the two box plots describe the sales performance of the two departments.
Answer:
By comparing two box plots, the sales are much quite closer to each other. There is not much difference between the women’s sales department and men’s sales department.
Question 25.
Calculate the mean sales figure for each of the two departments. Give your answers to the nearest dollar when you can.
Answer:
The data set for women: 10, 15, 8, 12, 28, 34, 36, 18, 14, 16, 27, 40
Mean=sum of observations/total number of observations.
Mean of women sale=10+15+8+12+28+34+36+18+14+16+27+40/12
Mean of women sale=258/12
mean of women sale=21.5
The data set for men: 8, 10, 11, 15, 20, 30, 24, 14, 10, 9, 17, 28
Mean of men’s sale=8+10+11+15+20+30+24+14+10+9+17+28/12
Mean of men’s sale=196/12
mean of men’s sale=16.3
Question 26.
Calculate the mean absolute deviation for each of the two departments. Give your answers to the nearest dollar.
Answer:
To understand Mean Absolute Deviation, let us split both the words and try to figure out their meaning. ‘Mean’ refers to the average of the observations and deviation implies departure or variation from a preset standard. When put together, we can define mean deviation as the mean distance of each observation from the mean of the data.
formula:
The ratio of the sum of all absolute values of deviation from central measure to the total number of observations.
M.A. D = (Σ Absolute Values of Deviation from Central Measure) / (Total Number of Observations)
Calculate MAD:
Steps to find the mean deviation from mean:
(i)Find the mean of the given observations.
(ii)Calculate the difference between each observation and the calculated mean
(iii)Evaluate the mean of the differences obtained in the second step.
This gives you the mean deviation from the mean.
The data set for women: 10, 15, 8, 12, 28, 34, 36, 18, 14, 16, 27, 40
Mean=sum of observations/total number of observations.
Mean of women sale=10+15+8+12+28+34+36+18+14+16+27+40/12
Mean of women sale=258/12
mean of women sale=21.5
|10-21.5|=11.5
|15-21.5|=6.5
|8-21.5|=13.5
|12-21.5|=9.5
|28-21.5|=6.5
|34-21.5|=12.5
|36-21.5|=14.5
|18-21.5|=3.5
|14-21.5|=7.5
|16-21.5|=5.5
|27-21.5|=5.5
|40-21.5|=18.5
now calculate mean for obtained differences:
MAD=11.5+6.5+13.5+9.5+6.5+12.5+14.5+3.5+7.5+5.5+5.5+18.5/12
MAD=115/12
MAD of women sale dapartment=9.58
The data set for men: 8, 10, 11, 15, 20, 30, 24, 14, 10, 9, 17, 28
Mean of men’s sale=8+10+11+15+20+30+24+14+10+9+17+28/12
Mean of men’s sale=196/12
mean of men’s sale=16.3
|8-16.3|=8.3
|10-16.3|=6.3
|11-16.3|=5.3
|15-16.3|=1.3
|20-16.3|=3.7
|30-16.3|=13.7
|24-16.3|=7.7
|14-16.3|=2.3
|10-16.3|=6.3
|9-16.3|=7.3
|17-16.3|=0.7
|28-16.3|=11.7
Now calculate the mean for obtained differences:
MAD=8.3+6.3+5.3+1.3+3.7+13.7+7.7+2.3+6.3+7.3+0.7+11.7/12
MAD=74.6/12
MAD of men’s sales department=6.21
Question 27.
Math Journal By comparing the means and the mean absolute deviations of the two clothing departments, what can you infer about their variability in sales?
Answer:
mean of women sale=21.5
mean of men’s sale=16.3
MAD of women sale dapartment=9.58
MAD of men’s sales department=6.21
MAD to mean ratio for women department:
9.58/21.5*100%
=44.6%
MAD to mean ratio for men’s department:
6.21/16.3*100%
=38.1%
By comparing all these, we can say the MAD to mean ratio for the women department is 44.6% and that of the men’s department is 38.1%. These two ratios show that the sales in the women department are slightly more varied than the sales in the men’s department.