Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 3 Lesson 3.4 Real-World Problems: Fractions and Decimals to finish your assignments.
Math in Focus Grade 6 Course 1 A Chapter 3 Lesson 3.4 Answer Key Real-World Problems: Fractions and Decimals
Math in Focus Grade 6 Chapter 3 Lesson 3.4 Guided Practice Answer Key
Solve.
Question 1.
The cost of carpeting a square yard is $8.60. How carpet 9.7 square yards?
9.7 × $
= $
It costs $ to carpet 9.7 square yards.
Answer:
9.7 × $8.60 = $83.42
It costs $83.42 to carpet 9.7 square yards.
Explanation:
The cost of carpeting a square yard is $8.60.
Cost of carpet 9.7 square yards
9.7 × $8.60 = $83.42
It costs $83.42 to carpet 9.7 square yards.
Question 2.
A roll of cloth 12 meters long is cut into smaller pieces of the same size. Each piece is 0.75 meter long. How many small pieces of cloth can be cut from the 12-meter roll?
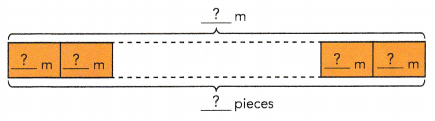
12 
=
small pieces of cloth can be cut from the 12-meter roll.
Answer:
12 ÷ 0.75 = 16
16 small pieces of cloth can be cut from the 12-meter roll.
Explanation:
A roll of cloth 12 meters long is cut into smaller pieces of the same size.
Each piece is 0.75 meter long.
Number of small pieces of cloth can be cut from the 12-meter roll
12 ÷ 0.75 = 16
Question 3.
Rosie buys 2.24 pounds of sliced ham to make sandwiches. She uses 0.16 pound for a sandwich. How many sandwiches can Rosie make?
÷ =
Rosie can make sandwiches.
Answer:
2.24÷ 0.16 = 14
Rosie can make 14 sandwiches.
Explanation:
Rosie buys 2.24 pounds of sliced ham to make sandwiches.
She uses 0.16 pound for a sandwich.
Number of sandwiches can Rosie make
2.24 ÷ 0.16 = 14
Question 4.
Bryce has $12.75. She wants to buy gifts for friends at a souvenir shop. If each souvenir costs $0.85, how many souvenirs can Bryce buy?
$ $ =
Bryce can buy souvenirs.
Answer:
$12.75 ÷ $0.85 = 15
Bryce can buy 15 souvenirs.
Explanation:
Bryce has $12.75.
She wants to buy gifts for friends at a souvenir shop.
Each souvenir costs $0.85,
Number of souvenirs can Bryce buy
$12.75 ÷ $0.85 = 15
Question 5.
A paper artist uses 18 paper rectangles for a collage. He uses 6 of them for the border of the artwork. He then cuts the remaining paper rectangles into equal strips, each \(\frac{1}{4}\) of a paper rectangle. How many strips of paper does he cut?
Answer:
48 strips of paper
Explanation:
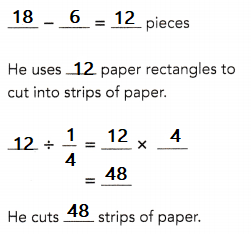
A paper artist uses 18 paper rectangles for a collage.
He uses 6 of them for the border of the artwork.
He then cuts the remaining paper rectangles into equal strips, each \(\frac{1}{4}\) of a paper rectangle
Total strips of paper he cut
18 – 6 = 12
12 ÷ \(\frac{1}{4}\)
=48
Question 6.
Sophie buys a roll of string that is 20 meters long. She uses 3 meters of string to tie a parcel. She then cuts the remaining string into equal pieces, each \(\frac{1}{2}\) meter long. How many pieces does Sophie cut?
÷ \(\frac{?}{?}\) = ×
=
Sophie cuts pieces.
Answer:
Sophie cuts 34 pieces.
Explanation:
Sophie buys a roll of string that is 20 meters long.
She uses 3 meters of string to tie a parcel.
20 – 3 = 17 mtrs
the roll of string after use 3 mtrs is 17 mtrs
17 ÷ \(\frac{1}{2}\) = 17 × 2
= 34
Sophie cuts 34 pieces.
Question 7.
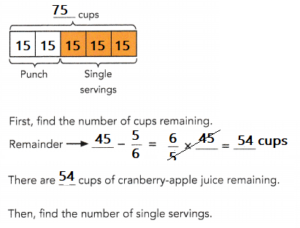
Andrea buys 75 cups of cranberry-apple juice for a party. She uses \(\frac{2}{5}\) of the juice to make punch. She then uses the remaining juice to pour single servings that are \(\frac{5}{6}\) cup each. How many single servings does Andrea pour?
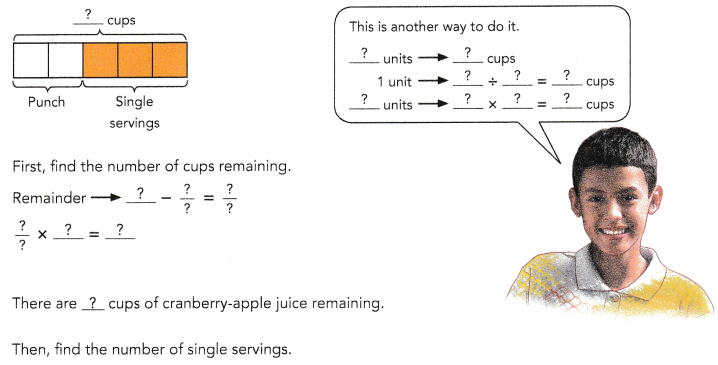
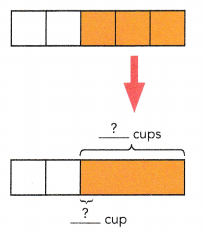
The remaining juice is poured into single servings that are \(\frac{5}{6}\) cup each.
÷ \(\frac{?}{?}\) = × \(\frac{?}{?}\)
=
Andrea pours single servings.
Answer:
The remaining juice is poured into single servings that are \(\frac{5}{6}\) cup each.
45 ÷ \(\frac{5}{6}\) = 45 × \(\frac{6}{5}\)
= 54
Andrea pours 54 single servings.
Explanation:
Andrea buys 75 cups of cranberry-apple juice for a party.
She uses \(\frac{2}{5}\) of the juice to make punch.
She then uses the remaining juice to pour single servings that are \(\frac{5}{6}\) cup each.
Number of single servings does Andrea pour
Andrea pours 54 single servings.
Question 8.
Meredith bakes 5 pumpkin pies. She cuts the pies into quarters and distributes the pieces equally among her neighbors. Each neighbor receives \(\frac{3}{4}\) of a pie.
a) How many neighbors does Meredith distribute the pies to?
5 ÷ \(\frac{3}{4}\) = × \(\frac{?}{?}\)
=
Meredith distributes the pies to neighbors.
How many neighbors does Meredith distribute the pies to?
Answer:
6\(\frac{2}{3}\)
Explanation:
5 ÷ \(\frac{3}{4}\) = 5 × \(\frac{4}{3}\)
= \(\frac{20}{3}\)
= 6\(\frac{2}{3}\)
Meredith distributes the pies to 6 neighbors.
b) What fraction of a pie is left?
× \(\frac{3}{4}\) =
5 – =
of a pie is left.
Answer:
\(\frac{1}{2}\) pie is left over.
Explanation:
\(\frac{1}{2}\) ÷ 6
= \(\frac{1}{2}\) x \(\frac{1}{6}\)
= \(\frac{1}{12}\)
c) What is the total amount of pie each neighbor will receive if the remainder is divided evenly and distributed to each neighbor?
5 ÷ =
Each neighbor will receive of a pie in total.
Answer:
Each neighbor will receive \(\frac{5}{6}\) of each pie.
Explanation:
Meredith bakes 5 pumpkin pies.
She cuts the pies into quarters and distributes the pieces equally among her neighbors.\(\frac{3}{4}\) + \(\frac{1}{12}\)
= \(\frac{9}{12}\) + \(\frac{1}{12}\)
= \(\frac{10}{12}\)
= \(\frac{5}{6}\)
Question 9.
Some bottles containing \(\frac{2}{5}\) gallon of water each are used to fill a 7-gallon container. How many of these bottles are needed to fill the container with water to its brim?
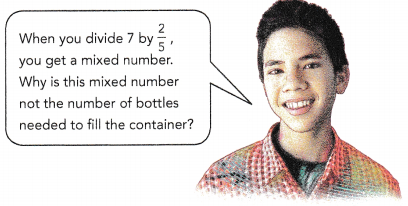
7 ÷ \(\frac{2}{5}\) = × \(\frac{?}{?}\)
=
bottles are needed to fill the container with water to its brim.
Answer:
7 ÷ \(\frac{2}{5}\) = 7 × \(\frac{5}{2}\)
= \(\frac{35}{2}\)
17 \(\frac{1}{2}\) bottles are needed to fill the container with water to its brim.
Explanation:
Bottles containing \(\frac{2}{5}\) gallon of water used to fill a 7-gallon container.
Number of bottles are needed to fill the container with water to its brim
7 ÷ \(\frac{2}{5}\) = 7 × \(\frac{5}{2}\)
= \(\frac{35}{2}\)
= 17 \(\frac{1}{2}\)
Question 10.
Lilian has a part-time job. Each month, she spends \(\frac{1}{3}\) of her earnings on clothes, saves \(\frac{3}{8}\) of the remainder, and spends the rest of her earnings on food.
a) What fraction of her earnings does she spend on food?
b) If she earns $540, how much does she spend on food each month?
Method 1
a)
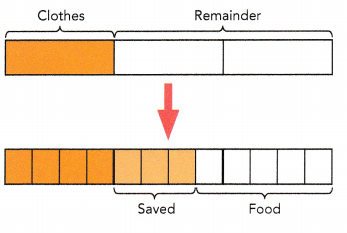
The model shows that:
She spends \(\frac{?}{?}\) of her earnings on food.
Answer:
She spends \(\frac{5}{8}\) of her earnings on food.
b) units → $540
1 unit → $ ÷ = $
units → × $ = $
She spends $ on food each month.
Answer:
She spends $225 on food each month.
Explanation:
12 units → $540
1 unit → $540 ÷ 12 = $45
5 units → 5 × $45 = $225
She spends $225 on food each month.
Method 2
a)
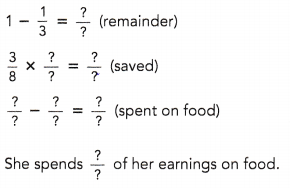
Answer:
She spends \(\frac{5}{8}\)
Explanation:
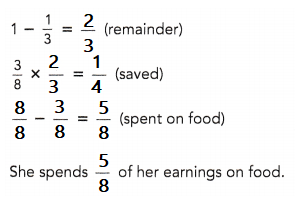
b) \(\frac{?}{?}\) × $540 = $
She spends $ on food each month.
Answer:
$225
Explanation:
540 x (1/3) = 180 for cloths
540 – 180 = 360
\(\frac{5}{8}\) × $360 = $225
She spends $225 on food each month.
Question 11.
\(\frac{2}{3}\) of a square is colored green. Asha cuts this green part into a number of pieces so that each piece is \(\frac{1}{9}\) of the whole square.
a) Find the number of pieces Asha has.
\(\frac{?}{?}\) ÷ \(\frac{?}{?}\) = \(\frac{?}{?}\) ×
=
Asha has pieces.
Answer:
Asha has 6 pieces.
Explanation:
\(\frac{2}{3}\) ÷ \(\frac{1}{9}\) = \(\frac{2}{3}\) × 9
= 6
Asha has 6 pieces.
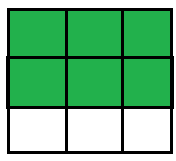
b) If the area of the square is 45 square inches, what is the area of each piece?
Area of green part = \(\frac{?}{?}\) × 45 = in.2
Area of each piece = ÷ = in.2
The area of each piece is square inches.
Answer:
The area of each piece is 5 square inches.
Explanation:
Area of green part = \(\frac{1}{9}\) × 45 = 5 in.2
Area of each piece = 45 ÷ 9 = 5 in.2
The area of each piece is 5 square inches.
Question 12.
\(\frac{3}{5}\) of the students in a class were boys. The teacher divided the boys equally into groups so that each group of boys had \(\frac{1}{10}\) of the number of students in the class. The teacher then divided the girls equally into groups such that each group of girls had \(\frac{1}{5}\) of the number of students in the class.
a) Find the number of groups of boys and the number of groups of girls.
There were groups of boys and groups of girls.
Answer:
There were 6 groups of boys and 2 groups of girls.
Explanation:
b) If there were 16 girls in the class, how many boys were there ¡n each group?
\(\frac{2}{5}\) of the class → 16 students
\(\frac{1}{5}\) of the class → students
\(\frac{3}{5}\) of the class → students
÷ 6 =
There were boys in each group.
Answer:
There were 4 boys in each group.
Explanation:
\(\frac{2}{5}\) of the class → 16 students
\(\frac{1}{5}\) of the class → 8 students
\(\frac{3}{5}\) of the class → 24 students
24 ÷ 6 =
There were 4 boys in each group.
Math in Focus Course 1A Practice 3.4 Answer Key
Solve. Show your work.
Question 1.
An ounce of pine nuts costs $1.40. If Ellen buys 2.5 ounces of pine nuts, how much will she have to pay?
Answer:
$3.50
Explanation:
One ounce cost $1.40,
she needed 2 and a half ounces
so, 1.40 x 2.5 = $3.50
Question 2.
25 pints of apple juice are poured into \(\frac{1}{2}\) pint bottles. How many bottles can be filled with apple juice?
Answer:
50 bottles can be filled with apple juice
Explanation:
25 pints of apple juice are poured into \(\frac{1}{2}\) pint bottles.
25 ÷ \(\frac{1}{2}\)
= 25 x 2 = 50 bottles
Question 3.
40 pounds of sugar are repackaged into packets of \(\frac{1}{16}\) pound each. How many packets of sugar are there?
Answer:
640 packets of sugar
Explanation:
40 pounds of sugar are repackaged into packets of \(\frac{1}{16}\) pound each.
Total packets of sugar 40 ÷ \(\frac{1}{16}\)
= 40 x 16 = 640
Question 4.
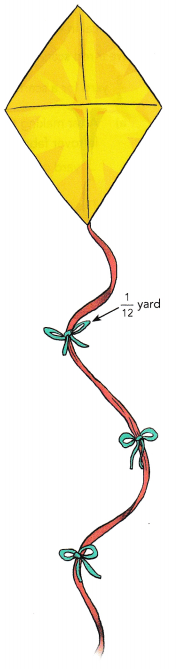
Tom used \(\frac{5}{8}\) yard of ribbon to tie weights on the tail of his kite. He cut the length of ribbon into equal pieces that were \(\frac{1}{12}\) yard long. How many pieces, each \(\frac{1}{12}\) yard long, did Tom cut from the \(\frac{5}{8}\) yard ribbon?
Answer:
7 \(\frac{2}{4}\) pieces
Explanation:
Tom used \(\frac{5}{8}\) yard of ribbon to tie weights on the tail of his kite.
He cut the length of ribbon into equal pieces that were \(\frac{1}{12}\) yard long.
Number of pieces = \(\frac{5}{8}\)÷ \(\frac{1}{12}\)
= 5 x \(\frac{12}{8}\)
= \(\frac{60}{8}\)
= 7 \(\frac{2}{4}\)
Question 5.
A carpenter has a 6-foot long board. He wants to cut the board into pieces that are \(\frac{4}{5}\) foot long.
a) How many pieces of length \(\frac{4}{5}\) foot can the carpenter cut from the board?
Answer:
7 \(\frac{2}{4}\) pieces
Explanation:
A carpenter has a 6-foot long board.
He wants to cut the board into pieces that are \(\frac{4}{5}\) foot long.
Number of pieces he get from the length \(\frac{4}{5}\)
6 ÷ \(\frac{4}{5}\)
= \(\frac{30}{4}\)
= 7 \(\frac{2}{4}\)
b) What length of the original board will be left after the carpenter has cut all the pieces that are \(\frac{4}{5}\) foot long?
Answer:
\(\frac{2}{4}\) pieces
Explanation:
A carpenter has a 6-foot long board.
He wants to cut the board into pieces that are \(\frac{4}{5}\) foot long.
Number of pieces he get from the length \(\frac{4}{5}\)
6 ÷ \(\frac{4}{5}\)
= \(\frac{30}{4}\)
= 7 \(\frac{2}{4}\)
Carpenter will cut 7 equal pieces of \(\frac{4}{5}\)
\(\frac{2}{4}\) is remaining.
Question 6.
A candle maker has 4\(\frac{1}{2}\) pounds of clear wax. He wants to cut the wax into pieces that are \(\frac{2}{3}\) pound each.
a) How many \(\frac{2}{3}\)-pound pieces can he divide the wax into?
Answer:
6 pieces
b) How much wax is left over?
Answer:
\(\frac{3}{4}\)
Explanation:
A candle maker has 4\(\frac{1}{2}\) pounds of clear wax.
He wants to cut the wax into pieces that are \(\frac{2}{3}\) pound each.
4\(\frac{1}{2}\) ÷ \(\frac{2}{3}\)
= \(\frac{9}{2}\) ÷ \(\frac{2}{3}\)
= \(\frac{9}{3}\) x \(\frac{2}{2}\)
= \(\frac{27}{4}\)
= 6 \(\frac{3}{4}\)
Question 7.
A roll of ribbon was 9 meters long. Kevin cut 8 pieces of ribbon, each of length 0.8 meter, to tie some presents. He then cut the remaining ribbon into some pieces, each of length 0.4 meter.
a) How many pieces of ribbon, each 0.4 meter in length, did Kevin have?
Answer:
6 pieces of 0.4 length
b) What was the length of ribbon left over?
Answer:
\(\frac{2}{4}\)
Explanation:
A roll of ribbon was 9 meters long.
Kevin cut 8 pieces of ribbon, each of length 0.8 meter, to tie some presents.
8 x 0.8 = 6.4 meters are used out of 6
So, 6 – 6.4 = 2.6
He then cut the remaining ribbon into some pieces, each of length 0.4 meter.
2.6 ÷ 0.4 = 6\(\frac{2}{4}\)
Question 8.
Mike has a large tropical fish collection. He gives \(\frac{2}{3}\) of his fish to a local high school. Then he gives \(\frac{2}{5}\) of the remaining fish to an elementary school. In the end, he has 30 fish left. How many fish did Mike have at first?
Answer:
150 fishes at first
Explanation:
Let, number of fishes = x
He gives \(\frac{2}{3}\) of his fish to a local high school.
That means \(\frac{1}{3}\) of his fish left.
Then he gives \(\frac{2}{5}\) of the remaining fish to an elementary school.
\(\frac{2}{3}\) x \(\frac{1}{3}\) x X = 30
\(\frac{3}{15}\)x X = 30
\(\frac{1}{5}\) x X = 30
X = 30 x 5 = 150
Question 9.
A costume designer has 40 yards of red fabric to make costumes for a musical in which 8 performers will wear red dresses and 14 people will wear red scarves. The costume maker uses 3\(\frac{1}{2}\) yards for each dress, and \(\frac{3}{4}\) yard for a scarf.
a) After making the dresses and scarves, the costume designer uses the leftover fabric to make some sashes for the dresses. If each sash uses \(\frac{1}{4}\) yard of fabric, how many sashes can be made?
Answer:
6 sashes
b) The costume designer decides to make the sashes a little smaller, so that each of the 8 dresses can have a sash. What fraction of a yard of fabric should the costume maker use to make each sash?
Answer:
\(\frac{1}{4}\) yard of fabric
Explanation:
Total fabric used for dresses= 8×3.5= 28 yards
Total fabric used for scarfs=14×0.75= 10.5 yards
Remaining fabric=40-28-10.5= 1.5 yards
Sashes made=1.5/0.25= 6 sashes.
Question 10.
Jack read \(\frac{1}{6}\) of a book on Monday and another \(\frac{1}{3}\) of it on Tuesday. He took another 4 days to finish reading the book. He read the same number of pages on each of the 4 days.
a) What fraction of the book did he read on each of the 4 days?
Answer:
Jack read \(\frac{1}{4}\)
b) If he read 40 pages on each of these 4 days, find the number of pages in the book.
Answer:
160 pages
Explanation:
Jack read \(\frac{1}{6}\) of a book on Monday and
another \(\frac{1}{3}\) of it on Tuesday
Total pages on both days \(\frac{1}{6}\) + \(\frac{1}{3}\)
= \(\frac{3}{6}\) = \(\frac{1}{2}\)
If he read 40 pages on each of these 4 days
Total number of pages in a book
40 x 4 = 160
fraction of the book he read on each of the 4 days
\(\frac{40}{160}\)
= \(\frac{1}{4}\)
Question 11.
The school librarian has $100 to spend on some books for the school. She wants to order many copies of the same book so an entire classroom can read the book. Each copy costs $3.95, Shipping for the books will be $6.95.
a) How many copies can the librarian order?
Answer:
23 books
Explanation:
100 – 6.95 = 93.05
93.05/3.95 =23.5
23.5 is rounded to 23 books
b) Describe how you can use estimation to decide if your answer to part a) is reasonable.
Answer:
23 books at cost of $4 is reasonable.
Explanation
25 book at cost $4 = $100
estimated cost of each book is $4
23 book cost is $92
$8 is for Shipping chargers
23 books at $4 is reasonable
Question 12.
Jason cycled for 3 hours. He cycled 7\(\frac{1}{2}\) miles each hour for the first two hours and the distance he cycled for the third hour was \(\frac{1}{4}\) of the total distance he cycled in 3 hours. What was the total distance Jason cycled in 3 hours?
Answer:
8\(\frac{2}{4}\) miles
Explanation:
Jason cycled 7\(\frac{1}{2}\) miles each hour for the first two hours and
the distance he cycled for the third hour was \(\frac{1}{4}\)
The total distance he cycled in 3 hours,
7\(\frac{1}{2}\) + \(\frac{1}{4}\)
= \(\frac{15}{4}\) + \(\frac{1}{4}\)
= \(\frac{34}{4}\)
= 8\(\frac{2}{4}\)
Question 13.
The length of a field was 20 yards. Mr. Matsumoto planted a row of peas every \(\frac{3}{4}\) yard.
a) How many rows of peas did Mr. Matsumoto plant?
Answer:
15 rows planted
b) What was the remaining length of field?
Answer:
5 yards
Explanation:
The length of a field was 20 yards.
Mr. Matsumoto planted a row of peas every \(\frac{3}{4}\) yard
20x \(\frac{3}{4}\) yard
= \(\frac{60}{4}\) = 15
Remaining length of the field 20 – 15 = 5 yards
Question 14.
A sign in an elevator says the elevator can lift up to 450 kilograms. John has 10 boxes that weigh 13.75 kilograms each, and a number of additional boxes that weigh 15.5 kilograms each. If he puts the 10 boxes on the elevator, how many of the additional boxes can be lifted in the same load?
Answer:
20 additional boxes
Explanation:
Weight of each box = 13.75 kg
Weight of 10 boxes = 13.75 x 10 = 137.5 kg
Space left in the box can be adjusted = 450 – 137.5 = 312.5 kg
Weight of additional boxes = 15.5 kg
Additional boxes can be lifted in the same load = 312.5 + 15.5 = 20.1 kg
Question 15.
Ken had a number of colored marbles in a bag. \(\frac{1}{4}\) of the marbles were red, \(\frac{2}{3}\) of the remaining marbles were blue, and the rest were yellow. Given that there were 120 red and yellow marbles altogether, how many marbles were there in the bag?
Answer:
240 marbles
Explanation
\(\frac{1}{4}\) = 0.25 of the marbles were red,
\(\frac{2}{3}\) x 0.75 = 0.5 of the remaining marbles were blue,
rest are yellow
1 – [0.25 + 0.5] = 0.25 [yellow]
0.25 + 0.25 = 0.5
RED + YELLOW = 120
total
RED + YELLOW+ BLUE = 120 + 120 = 240
Question 16.
Rachel used \(\frac{3}{8}\) of her money to buy some blouses and \(\frac{2}{5}\) of the remainder to buy 2 pairs of pants. A pair of pants costs 3 times as much as a blouse. How many blouses did she buy?
Answer:
9 blouses
Explanation:
Rachel used \(\frac{3}{8}\) of her money to buy some blouses,
If total cloth is 8 parts, out of which 3 parts are used.
So, \(\frac{5}{8}\) left.
She used \(\frac{2}{5}\) of the remainder to buy 2 pairs of pants.
\(\frac{2}{5}\) x \(\frac{5}{8}\)
= \(\frac{10}{40}\)
= \(\frac{1}{4}\) used for 2 pairs of pants \(\frac{1}{8}\) each.
A pair of pants costs 3 times as much as a blouse.
So, each blouse cost \(\frac{1}{24}\)
Number of blouses she buy are
\(\frac{3}{8}\) x \(\frac{24}{1}\)
= \(\frac{72}{8}\)
= 9
Question 17.
Sheila went shopping and spent $120 on a coat. She then used \(\frac{2}{3}\) of the remaining money to buy a dress. She was left with \(\frac{1}{5}\) of her original amount of money. How much did Sheila have at first?
Answer:
let Sheila has $M first
Explanation:
Let M = original amount of money
M – 120 – [(2/5)(M-120)] = M/5
M – 120 – 2M/5 + 48 = M/5
M – 2M/5 – M/5 = 120 – 48
5M/5 – 2M/5 – M/5 = 72
2M/5 = 72
M = 72(5/2)
M = 36(5)
M = $180
Sheila started with $180
180 – 120 = 60
60 – (2/5)(60) = 36
180(1/5) = 36
She has $36 left and that is indeed 1/5 of the original $180.
Brain @ Work
Question 1.
Alex, Beth and Carol share a sum of money. Alex receives 0.7 of the sum of money. Beth and Carol receive the rest of the money. If Beth receives \(\frac{5}{12}\) of the money shared by both her and Carol, and Carol receives $847, how much money does Alex get?
Answer:
Alex’s share = $3,388
Explanation:
Let the total money be X ,
Alex = 0.70 or \(\frac{7}{10}\) of total amount
Share of Beth + Carol = 1 – share of Alex
= 1 – \(\frac{7}{10}\)
=\(\frac{3}{10}\)
Beth and Carol = \(\frac{3}{10}\) of total amount
Beth = \(\frac{5}{12}\) of the \(\frac{3}{10}\) of total amount
Carol = \(\frac{7}{12}\) of the \(\frac{3}{10}\) of total amount
Since Carol receives $847,
Share of Beth + Carol = share of Carol ÷ \(\frac{7}{12}\)
= 847 ÷ \(\frac{7}{12}\)
= 847 x \(\frac{12}{7}\)
= $1425
Total amount = Alex +Beth + Carol
we know,
Beth + Carol = \(\frac{3}{10}\) x total amount = $1425
total amount = 1452 ÷ \(\frac{3}{10}\)
= $1,452 x \(\frac{10}{3}\)
= 4,840
Total amount = Alex + Beth + Carol
4840 = Alex + 1452
Alex = 4840 – 1452
Alex = 3388
Alex’s share = $3,388