Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 5 Rates to finish your assignments.
Math in Focus Grade 6 Course 1 A Chapter 5 Answer Key Rates
Math in Focus Grade 6 Chapter 5 Quick Check Answer Key
Multiply
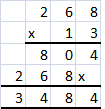
Question 1.
268 × 13
Answer:
3,484
Explanation:
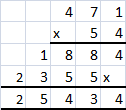
Question 2.
54 × 471
Answer:
25,434
Explanation:
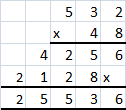
Question 3.
532 × 48
Answer:
25,536
Explanation:
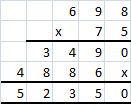
Question 4.
75 × 698
Answer:
52,350
Explanation:
Find each product. Express the product in simplest form.
Question 5.
4 × \(\frac{5}{32}\)
Answer:
\(\frac{5}{8}\)
Explanation:
The first step when multiplying fractions is to multiply the two numerators.
The second step is to multiply the two denominators.
Finally, simplify the new fractions.
= 4 × \(\frac{5}{32}\)
= 4 x 5 ÷ 32
= \(\frac{20}{32}\)
= \(\frac{5}{8}\)
Question 6.
\(\frac{7}{12}\) × 36
Answer: 21
Explanation:
The first step when multiplying fractions is to multiply the two numerators.
The second step is to multiply the two denominators.
Finally, simplify the new fractions.
\(\frac{7}{12}\) x 36
= \(\frac{(7)(36)}{12}\)
= \(\frac{252}{12}\) = 21
Question 7.
3\(\frac{2}{7}\) × 5
Answer:
\(\frac{115}{7}\)
Explanation:
The first step when multiplying fractions is to multiply the two numerators.
The second step is to multiply the two denominators.
Finally, simplify the new fractions.
3\(\frac{2}{7}\) x 5
= \(\frac{23}{7}\) x 5
= \(\frac{115}{7}\)
Question 8.
9\(\frac{1}{2}\) × 8
Answer: 76
Explanation:
The first step when multiplying fractions is to multiply the two numerators.
The second step is to multiply the two denominators.
Finally, simplify the new fractions.
9\(\frac{1}{2}\) x 8
= \(\frac{19}{2}\) x 8
= \(\frac{152}{2}\) = 76
Find each product. Express the product in simplest form.
Question 9.
\(\frac{2}{7}\) × \(\frac{63}{84}\)
Answer:
\(\frac{3}{14}\)
Explanation:
The first step when multiplying fractions is to multiply the two numerators.
The second step is to multiply the two denominators.
Finally, simplify the new fractions.
\(\frac{2}{7}\) x \(\frac{63}{84}\)
= \(\frac{(2)(63)}{(7)(84)}\)
= \(\frac{126}{588}\)
= \(\frac{3}{14}\)
Question 10.
\(\frac{11}{18}\) × \(\frac{3}{44}\)
Answer: 24
Explanation:
The first step when multiplying fractions is to multiply the two numerators.
The second step is to multiply the two denominators.
Finally, simplify the new fractions.
\(\frac{11}{18}\) x \(\frac{3}{44}\)
= \(\frac{11 X3}{18 x 44}\)
= \(\frac{33}{792}\) = 24
Find each quotient. Express the quotient in simplest form.
Question 11.
\(\frac{6}{7}\) ÷ 30
Answer:
\(\frac{1}{35}\)
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction.
A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
\(\frac{6}{7}\) ÷ 30
= \(\frac{6}{7}\) ÷ \(\frac{30}{1}\)
= \(\frac{6}{7 X 30}\)
= \(\frac{6}{210}\)
= \(\frac{2}{70}\)
= \(\frac{1}{35}\)
Question 12.
72 ÷ \(\frac{9}{10}\)
Answer:
\(\frac{1}{80}\)
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction.
A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
\(\frac{9}{10}\) ÷ 72
= \(\frac{9}{10}\) ÷ \(\frac{72}{1}\)
= \(\frac{9}{10 X 72}\)
= \(\frac{9}{720}\)
= \(\frac{1}{80}\)
Question 13.
\(\frac{7}{9}\) ÷ 49
Answer:
\(\frac{1}{63}\)
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction.
A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
\(\frac{7}{9}\) ÷ 49
= \(\frac{7}{9}\) ÷ \(\frac{49}{1}\)
= \(\frac{7}{9 X 49}\)
= \(\frac{7}{441}\)
= \(\frac{1}{63}\)
Question 14.
56 ÷ \(\frac{8}{11}\)
Answer:
\(\frac{1}{77}\)
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction.
A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
\(\frac{8}{11}\) ÷ 56
= \(\frac{8}{11}\) ÷ \(\frac{56}{1}\)
= \(\frac{8}{11 X 56}\)
= \(\frac{8}{616}\)
= \(\frac{1}{77}\)
Question 15.
\(\frac{4}{9}\) ÷ \(\frac{36}{135}\)
Answer:
\(\frac{5}{3}\)
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction.
A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
= \(\frac{4}{9}\) ÷ \(\frac{36}{135}\)
= \(\frac{4}{9}\) x \(\frac{135}{36}\)
= \(\frac{4 X 135}{9 X 36}\)
= \(\frac{540}{324}\)
= \(\frac{5}{3}\)
Question 16.
\(\frac{77}{92}\) ÷ \(\frac{11}{42}\)
Answer:
\(\frac{5467}{56}\) OR 97\(\frac{35}{56}\)
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction.
A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
= \(\frac{77}{92}\) ÷ \(\frac{11}{142}\)
= \(\frac{77}{92}\) x \(\frac{142}{11}\)
= \(\frac{77 X 142}{92 X 11}\)
= \(\frac{10,934}{1,012}\)
= \(\frac{5467}{56}\)
Find the value of each set.
Question 17.
If 7 units represent 98 liters, find the value of 15 units.
Answer:
210 liters
Explanation:
First, find out the value of 1 unit,
98 ÷ 7 = 14 liters.
Then, multiply 14 by 15 which is 210 liters.
Question 18.
If 13 units represent 143 square meters, find the value of 24 units.
Answer:
264 square meters
Explanation:
First, find out the value of 1 unit,
143 ÷ 13 = 11 liters.
Then, multiply 11 by 24 which is 264 liters.
Express each ratio in simplest form.
Question 19.
4 km : 370 m
Answer:
400m : 37m
Explanation:
The simplest form of the ratio is when the numbers are expressed as natural numbers with no common factors.
convert km in m
1km = 1000m
4 km : 370 m
4000m : 370
The common factor in the above equation is 2, 5.
Question 20.
66 L : 120 mL
Answer:
550mL : 1mL
Explanation:
The simplest form of the ratio is when the numbers are expressed as natural numbers with no common factors.
Convert liter into milliliters
1 L = 1000mL
66 L : 120 mL
66000 : 120mL
550mL : 1mL
The common factor in the above equation is 2, 3, 5.
Question 21.
15 in. : 5 ft
Answer:
12ft : 1ft
Explanation:
The simplest form of the ratio is when the numbers are expressed as natural numbers with no common factors.
Convert inches to feet
1 feet = 12 inches
15 in. : 5 ft
= 15 x 12 : 5
= 60 : 5
= 12 : 1
The common factor in the above equation is 5.
Question 22.
270 qt: 105 gal
Answer:
Explanation:
The simplest form of the ratio is when the numbers are expressed as natural numbers with no common factors.
Convert quarter to gallon
1gal = 4 qt
270 qt : 105 gal
= 270 : 105 x 4
= 270 : 420
= 9 : 14
The common factor in the above equation is 30.
Find two ratios equivalent to each ratio.
Question 23.
4 : 9
Answer:
8 : 18
Explanation:
Equivalent ratios are ratios that make the same comparison of numbers.
Two ratios are equivalent if one can be expressed as a multiple of the other.
multiples of 4 (4, 8, 12, 16, 20, 24, 28, . . . ) and 9 (9, 18, 27, 36, . . . . )
Question 24.
5 : 13
Answer:
10 : 26
Explanation:
Equivalent ratios are ratios that make the same comparison of numbers.
Two ratios are equivalent if one can be expressed as a multiple of the other.
multiples of 5 (5, 10, 15, 20, . . . ) and 13 (13, 26, 39, 52, 65, 78, 91, . . . . )