Math in Focus Grade 7 Chapter 8 Lesson 8.5 Answer Key Real-World Problems: Composite Solids

This handy Math in Focus Grade 7 Workbook Answer Key Chapter 8 Lesson 8.5 Real-World Problems: Composite Solids detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 8 Lesson 8.5 Answer Key Real-World Problems: Composite Solids

Math in Focus Grade 7 Chapter 8 Lesson 8.5 Guided Practice Answer Key

Solve.

Question 1.
A composite solid is made up of a cone and a cylinder. The slant height of the cone is 25 centimeters. The height of the cylinder is 15 centimeters and its radius is 12 centimeters. The height of the solid is 37 centimeters. Use 3.14 as an approximation for π.

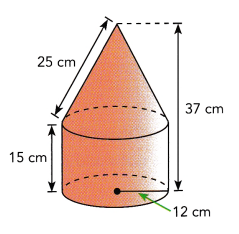
a) Find the volume of the composite solid to the nearest cubic centimeter.
Volume of the cylinder:
πr²h = ∙ ∙ Use the formula for volume of a cylinder.
= cm³ Evaluate .

Volume of the cone:
Height of cone = –
= cm
\(\frac{1}{3}\) πr²h = \(\frac{1}{3}\) ∙ ∙ ∙ ∙ Use the formula for the volume of a cone.
= cm³ Multiply.
Volume of the composite solid:
+ = Add the volumes of the cylinder and the cone.
≈ cm³ Multiply and round.
The volume of the composite solid is about cubic centimeters.
Answer:  The volume of the composite solid is about 10,098 cm³
We are given:
l = 25
h_cylinder = 15
H = 37
r = 12
Use the formula for the volume of a cylinder:
V_cylinder = πr²h_cylinder
= π · 12² · 15
Evaluate:
= 2,160π cm³
The height of the cone:
h_cone = H – h_cylinder
= 37 – 15
= 22 cm
Use the formula for the volume of a cone:
V_cone = \(\frac{1}{3}\)πr²h_cone
= \(\frac{1}{3}\) · π · 12² · 22
Multiply:
= 1,056π cm³
Find the volume of the composite solid by adding the volumes of the cylinder and the cone:
V = V_cylinder + V_cone
= 2,160π + 1,056π
= 3,216π cm³
Multiply and round:
≈ 10,098 cm³

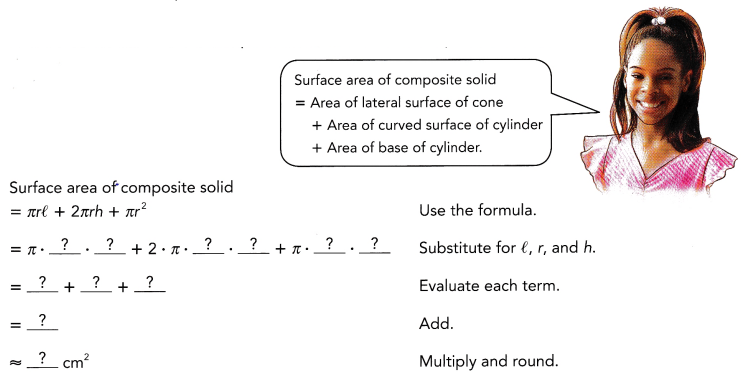
b) Find the surface area of the composite solid to the nearest square centimeter.

The surface area of the composite solid is about square centimeters.
Answer: The surface area of the composite solid is about  2,525 cm^2.
Use the formuLas for the surface areas:
S = πrl + 2πrh_cylinder + πr²
Substitute for r, l, h_cylinder
= π · 12 · 25 + 2π · 12 · 15 + π · 12²
Evaluate each term:
= 300π + 360π + 144π
Add:
= 804π
Multiply and round:
≈ 804 · 3.14 ≈ 2,525 cm²

Question 2.
A birdhouse looks like a cube with a square pyramid on top. As shown, the birdhouse has a circular entrance with a diameter of 4 inches. Find the exterior surface area of the birdhouse.

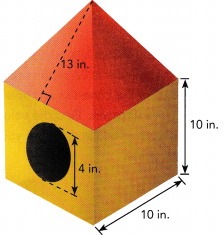
Answer: The exterior surface area of the birdhouse is 647.4 in²
Determine the Lateral surface area of the pyramid:
S₁ = 4 · \(\frac{1}{2}\) · 10 · 13 = 260 in²
Determine the radius of the entrance:
r = \(\frac{4}{2}\) = 2
Determine the lateral surface area of the house:
S₂ = 4 · 10 · 10 – π · 2² ≈ 387.4 in²
Compute the exterior surface area of the house:
S = S₁ + S₂ = 260 + 387.4 = 647.4 in²
= 647.4 in²

Question 3.
The solid shown is a cylinder with a cone-shaped hole. The diameter of the cylinder is 22 centimeters. Its height is 15 centimeters. The radius of the cone-shaped hole is 7 centimeters and the height is 10 centimeters. Find the volume of the solid. Use 3.14 as an approximation for π. Round your answer to the nearest cubic centimeter.

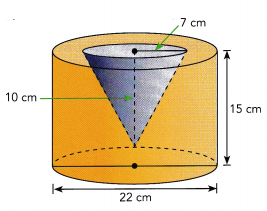
Answer: The volume of the solid is  5. 187 cm³
Determine the radius R of the cylinder:
R = \(\frac{22}{2}\) = 11 cm
Determine the volume of the cylinder
V_cylinder = πR²h = π · 11² ·  15 = 1, 815π cm²
Determine the volume of the cone:
V_cone = \(\frac{1}{3}\)πR²h = \(\frac{1}{3}\) · π · 7² · 10 ≈ 163π cm³
Determine the volume of the solid:
V = V_cylinder – V_cone
= 1,815π – 163π
= 1,652π
≈ 3.14 · 1,652
≈ 5. 187 cm³

Math in Focus Course 2B Practice 8.5 Answer Key

For this practice, you may use a calculator and use 3.14 as an approximation for π. Round your answers to the nearest tenth when you can.

Solve.

Question 1.
Jack has a cylindrical block that has a radius of 0.6 cm and is 22 centimeters long. He puts together 8 such blocks to form the composite solid shown. What is the volume of the composite solid?

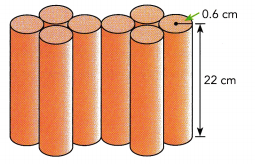
Answer: The volume of the composite solid is 199 cm³
We are given the cylinder:
r = 0.6
h = 22
Determine the volume of one cylinder:
V_cylinder = πr²h ≈ 3.14 · 0.6² · 22
≈ 24.87 cm³
Determine the volume of the composite solid:
V_solid = 8V_cylinder = 8 · 24.87 ≈ 199 cm³

Question 2.
The trophy for a basketball tournament is made up of a miniature basketball attached to a rectangular prism. The radius of the basketball is 5 centimeters. The prism measures 8 centimeters by 5 centimeters by 15 centimeters. What is the volume of the trophy to the nearest cubic centimeter?

Answer: The volume of the trophy is 1,123 cm³
We are given:
r = 5
l = 8
w = 5
h = 15
Determine the volume of the sphere:
V_sphere = \(\frac{4}{3}\)πr³
≈ \(\frac{4}{3}\) · 3.14 · 5³
≈ 523 cm³
Determine the volume of the prism:
V_prism = lwh = 8 · 5 · 15 = 600 cm³
Determine the volume of the trophy:
V_trophy = V_sphere + V_prism
= 523 + 600
= 1,123 cm³

Question 3.
A necklace is made up of 50 spherical beads. Each bead has a radius of 8 millimeters.
a) What is the volume of the necklace?
Answer: The volume of the necklace is 107, 178.7 mm³
We are given the sphere:
r = 8
Determine the volume of a spherical bead:
V_bead = \(\frac{4}{3}\)πr³
≈ \(\frac{4}{3}\) · 3.14 · 8³
≈ 2,143.573
Determine the volume of the necklace:
V_necklace = 50 · V_bead
≈ 50 – 2. 143.573 ≈ 107, 178.7 mm³

b) What is the surface area of the necklace?
Answer: The surface area of the necklace is 40,192 mm²
Determine the surface area of a spherical bead:
S_bead = 4πr² ≈ 4 · 3.14 · 8²
≈ 803.84 mm²
Determine the surface area of the necklace:
S_necklace = 50 · S_bead
= 50 · 803.84
≈ 40,192 mm²

Question 4.
A crystal trophy is made up of a rectangular pyramid whose base is attached to the top of a rectangular prism. The base of the pyramid and the top of the prism are each 4 inches long and 3 inches wide. The height of the pyramid is 2.5 inches and the height of the prism is 9.5 inches. What is the volume of the crystal trophy?
Answer: The volume of the crystal trophy is 124 in³
We are given:
l = 4
w = 3
h_pyramid = 2.5
h_prism = 9.5
Determine the volume of the pyramid:
V_pyramid =\(\frac{1}{3}\) · lwh_pyramid 
= \(\frac{1}{3}\) · 4 · 3 · 2.5
= 10 in³
Determine the volume of the prism:
V_prism = lwh_prism = 4 · 3 · 9.5
= 114 in³
Determine the volume of the trophy:
V_trophy = V_pyramid + V_prism
= 10 + 114
= 124 in³

Question 5.
At a food stand, you can buy a paper cone filled with slush made of frozen juice. The slush forms a hemisphere on top of the cone, as shown. What is the volume of the cone of slush?

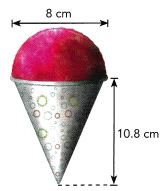
Answer: The volume of the cone of slush is 314.9 cm³
We are given:
d = 8
h = 10.8
Determine the radius:
r = \(\frac{d}{2}\) = \(\frac{8}{2}\) = 4
Determine the volume of the hemisphere:
V_hemisphere = \(\frac{1}{2}\) · \(\frac{4}{3}\) πr³
≈ \(\frac{2}{3}\) · 3.14 · 4³
≈ 134 cm³
Determine the volume of the cone:
V_cone = \(\frac{1}{3}\) πr²h
≈ \(\frac{1}{3}\) · 3.14 · 4² · 10.8
≈ 180.9 cm³
Determine the volume of the cone of slush:
V = V_hemisphere + V_cone
= 134 + 180.9
= 314.9 cm³

Question 6.
A wooden paper towel holder is composed of two cylinders. The diameter of the base is 12 .centimeters and its height is 2 centimeters. The combined height of the two cylinders is 30 centimeters. What is the volume of the paper towel holder?

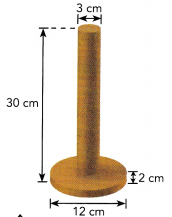
Answer: The volume of the paper towel holder is 438 cm³
We are given:
d₁ = 3
h₁ = 30
d₂ = 12
h₂ = 2
Determine the radius of the upper cylinder:
r₁ = \(\frac{d_{1}}{2}\) = \(\frac{3}{2}\) = 1.5
Determine the volume of the upper cylinder:
V₁ = πr₁²h₁ = π · 1 5² · 30 = 67.5π cm³
Determine the radius of the lower cylinder:
r₂ = \(\frac{d_{2}}{2}\) = \(\frac{12}{2}\) = 6
Determine the volume of the lower cylinder:
V₂ = πr₂²h₂ = π · 6² · 2 = 72π cm³
Determine the volume of the paper tower holder:
V = V₁ + V₂ = 67.5π + 72π
≈ 139.5π
≈ 139.5 · 3.14
≈ 438 cm³

Question 7.
The edge of the base of a square pyramid is 11 inches. The pyramid has a height of 14 inches. What is the volume of the composite solid formed when two such pyramids are joined at the base, as shown in the diagram?

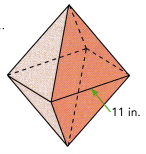
Answer: The volume of the composite solid is  1,129.3 in³
We are given:
L = 11
h = 14
Determine the volume of one pyramid:
V₁ = V₂ = \(\frac{1}{3}\)l²h = \(\frac{1}{3}\) · 11² · 14 ≈ 564.67 in³
Determine the volume of the composite solid:
V = V₁ + V₂ = 2V₁ = 2 · 564.67
≈ 1,129.3 in³

Question 8.
A clock in the shape of an hour glass is made up of two identical cones connected at their vertices. The radius of each cone is 7 centimeters. The combined height of the two cones is 11.8 centimeters. What is the volume of the clock?

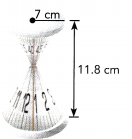
Answer: The volume of the clock is 605.2 cm³
We are given:
r = 7
H = 11.8
Determine the height of each cone:
h = \(\frac{H}{2}\) = \(\frac{11.8}{2}\) = 5.9
Determine the volume of one cone:
V₁ = V₂ = \(\frac{1}{3}\)πr²h =  \(\frac{1}{3}\) · π · 7² · 59
≈ 96.3677π
Determine the volume of the clock:
V = V₁ + V₂ = 2V₁ = 2 · 96.367π
≈ 192.734 · 3.14
≈ 605.2 cm³

Question 9.
Jason made a long pole by joining three different lengths of cylindrical poles together. Each pole has the same diameter of 18 cm. The diagram below is not drawn to scale.

a) What is the volume of the long pole?
Answer: The volume of the long pole is 8,393.2 cm³
We are given:
d = 18
h₁ = 7
h₂ = 11
h₃ = 15
Determine the radius
r = \(\frac{d}{2}\) = \(\frac{18}{2}\) = 9
Determine the volume of the tong pole:
V = V₁ + V₂ + V₃
= πr²h₁ + πr²h₂ + πr² h3
= πr²(h₁ + h₂ + h₃)
≈ 3.14 · 9² · (7 + 11 + 15)
≈ 8,393.2 cm³

b) What is the surface area of the long pole?
Answer: The surface area of the long pole is  2,373.8 cm²
Determine the surface area of the long pole
= 2πr² + 2πr(h₁ + h₂ + h₃)
= 2πr(r + h₁ + h₂ + h₃)
≈ 2 · 3.14 · 9(9 + 7 + 11 + 15)
≈ 2,373.8 cm²

Brain @ Work

How can you make the following cross-sections by slicing a cube? Use a computer drawing program or pencil and paper to show your answers for a) and b).
a) An isosceles triangle
Answer:
We take a point on one edge, then take two congruent segments from one of the vertices on the same edge on the other two edges
We draw the cross-section in the cube in the shape of an isosceles triangle:

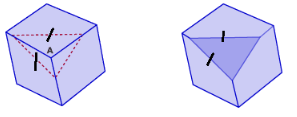
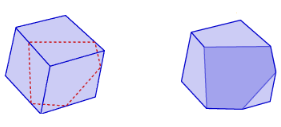
b) A regular hexagon
Answer:
To get a hexagon, we slice the cube with a plane going through alt six faces of the cube.
We draw the cross-section in the cube in the shape of a regular hexagon:

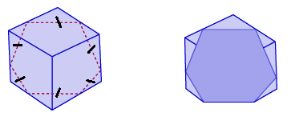
c) What other polygons can be cross-sections of a cube?
Answer:
The cross-section can be a quadrilateral when a plane crosses 4 faces of the cube:

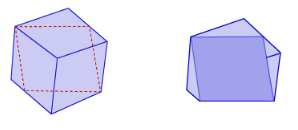
The cross-section can also be a pentagon when a plane crosses 5 faces of the cube: