Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 5 Practice 2 Using Letters as Numbers to finish your assignments.
Math in Focus Grade 5 Chapter 5 Practice 2 Answer Key Using Letters as Numbers
Write an expression for each situation.
Question 1.
Susan has 10 apples and 6 oranges. How many pieces of fruit does she have?
Answer:
10 + 6 = 16
She have 16 pieces of fruits.
Explanation:
Susan has 10 apples and 6 oranges. Add 10 apples with 6 oranges the sum is 16. She have 16 pieces of fruits.
Question 2.
Juan has x apples and 8 oranges. How many pieces of fruit does he have? Give your answer in terms of x.
Answer:
x + 8
He have x + 8 pieces of fruits.
Explanation:
Juan has x apples and 8 oranges. Add x apples with 8 oranges the sum is x + 8. He have x + 8 pieces of fruits.
Question 3.
Henry has $18. He spends $2. How much does he have left?
Answer:
$18 – $2 = $16
He have $16 left.
Explanation:
Henry has $18. He spends $2. Subtract $2 from $18 the difference is $16.
Question 4.
Katie has m dollars. She spends $5. How much does she have left? Give your answer in terms of m.
Answer:
(m – 5)$
She have $m – $5 left.
Explanation:
Katie has m dollars. She spends $5. The expression is $m – $5.
Write an expression for the situation.
Question 5.
Hugo has $20. He spends n dollars. How much does he have left? Give your answer in terms of n.
Answer:
$20 – $n
He have $20 – $n left.
Explanation:
Hugo has $20. He spends n dollars. He have $20 – $n left.
Write an algebraic expression for each of the following.
Example
Add 9 to y.
y + 9 or 9 + y
Question 6.
Add b to 11
Answer:
b + 11 or 11 + b
Explanation:
The algebraic expression for Add b to 11 is b + 11 or 11 + b.
Question 7.
Subtract 6 from c
Answer:
c – 6
Explanation:
The algebraic expression for Subtract 6 from c is c – 6.
Question 8.
Subtract p from 15.
Answer:
15 – p
Explanation:
The algebraic expression for Subtract p from 15 is 15 – p.
Question 9.
12 more than d.
Answer:
12 > d
Explanation:
The algebraic expression for 12 more than d is 12 > d.
Question 10.
15 less than g.
Answer:
15 < g
Explanation:
The algebraic expression for 15 less than g is 15 < g.
Evaluate each expression for the given values of y.

Answer:
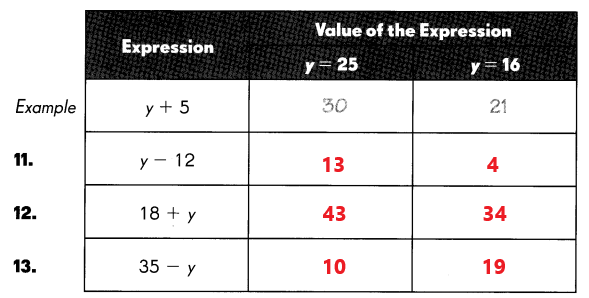
Question 11.
y – 12
Answer:
For y = 25
y – 12 = 25 – 12 = 13
For y = 16
y – 12 = 16 – 12 = 4
Explanation:
Place y = 25 in the expression y -12. Subtract 12 from 25 the difference is 13.
Place y = 16 in the expression y – 12. Subtract 12 from 16 the difference is 4.
Question 12.
18 + y
Answer:
For y = 25
18 + y = 18 + 25 = 43
For y = 16
18 + y = 18 + 16 = 34
Explanation:
Place y = 25 in the expression 18 + y. Add 18 to 25 the sum is 43.
Place y = 16 in the expression 18 + y . Add 18 to 16 the sum is 34.
Question 13.
35 – y
Answer:
For y = 25
35 – y = 35 – 25 = 10
For y = 16
35 – y = 35 – 16 = 19
Explanation:
Place y = 25 in the expression 35 – y. Subtract 25 from 35 the difference is 10.
Place y = 16 in the expression 35 – y. Subtract 16 from 35 the difference is 19.
Write each of the following in at least three other ways.
Example
![]()
Question 14.
18 × m _______
Answer:
The three other ways of 6n is m × 18, 18 groups of n, 18n.
Question 15.
75 groups of y _______
Answer:
The three other ways of 75 groups of y is 75y, 75 × y, y × 75.
Question 16.
y groups of 12 _______
Answer:
The three other ways of y groups of 12 is y12, y × 12, 12 × y.
Write an expression for each situation.
Question 17.
Julio has 4 boxes of pencils. There are 12 pencils in each box. How many pencils does Julio have?
Answer:
4 × 12 = 48
Julio have 48 pencils.
Explanation:
Julio has 4 boxes of pencils. There are 12 pencils in each box. Multiply 4 with 12 the product is 48. Julio have 48 pencils.
Question 18.
Tara has k boxes of pencils. There are 10 pencils in each box. How many pencils does Tara have? Give your answer in terms of k.
Answer:
k × 10 = 10k
Tara have 10k pencils.
Explanation:
Tara has k boxes of pencils. There are 10 pencils in each box. Multiply k with 10 the product is 10k. Tara have 10k pencils.
Write an expression for each situation.
Question 19.
A restaurant divided 20 gallons of lemonade among 4 containers. How much lemonade does each container contain?
Answer:
20 ÷ 4 = 5
Each container contains 5 lemonade.
Explanation:
A restaurant divided 20 gallons of lemonade among 4 containers. Divide 20 by 4 the result is 5. Each container contains 5 lemonade.
Question 20.
m gallons of lemonade are distributed equally among 3 people. How much lemonade does each person get? Give your answer in terms of m.
Answer:
m ÷ 3
Each person get m ÷ 3 lemonade.
Explanation:
m gallons of lemonade are distributed equally among 3 people. Divide m by 3. Each person get m ÷ 3 lemonade.
Question 21.
Multiply f and 6.
Answer:
f × 6 = 6f
Question 22.
Divide m by 5.
Answer:
m ÷ 5
Question 23.
Divide 22 by p.
Answer:
22 ÷ p
Evaluate each expression for t = 156.
Example
2t = 2 × D
= 2 × 156
= 312
Question 24.
\(\frac{t}{6}\) =
Answer:
For t = 156
t/6 = 156 /6 = 26
Explanation:
Place t = 156 in given expression t/6. Divide 156 by 6 the result is 26.
Question 25.
16t =
Answer:
For t = 156
16t = 16 × t = 16 × 156 = 2,496
Explanation:
Place t = 156 in given expression 6t. Multiply 16 with 156 the product is 2,496.
Question 26.
\(\frac{t}{13}\) =
Answer:
For t = 156
t/13= 156 /13 = 12
Explanation:
Place t = 156 in given expression t/13. Divide 156 by 13 the result is 12.
Write an algebraic expression for each situation.
Question 27.
A tank has x gallons of water. Ted adds 3 gallons of water into the tank. He pours the water equally into 4 smaller containers. How much water is in each container?
Answer:
Question 28.
Jenny has $15. She buys 2 books that cost m dollars each. How much does she have left?
Answer:
She have (15 – 2m)$ left.
Jenny has $15. She buys 2 books that cost m dollars each. She have (15 – 2m)$ left.
Write an algebraic expression for each situation.
Question 29.
Betty collected 400 food packages for charity. She gave g packages to an orphanage, and distributed the rest equally among 4 charities. How many packages did each charity get?
Answer:
Question 30.
To bake muffins, Matt needs x eggs for every 200 grams of flour. If he used 900 grams of flour, how many eggs did he use?
Answer:
Write an expression for each situation.
Example
Subtract 12 from the product of 8 and a.
8 × a – 12 = 8a – 12
Question 31.
Add 14 to the product of 3 and b.
Answer:
3 × b + 14 = 3b + 14
Explanation:
The expression for the situation add 14 to the product of 3 and b is 3b + 14.
Question 32.
Divide the product of 7 and d by 5.
Answer:
7 × d ÷ 5 = 7d ÷ 5
Explanation:
The expression for the situation divide the product of 7 and d by 5 is 7d ÷ 5.
Evaluate each expression for x = 5.
Example
13x – 4 = 13 × 5 – 4
= 65 – 4
= 61
Question 33.
5x + 12 =
Answer:
For x = 5
5x + 12 = 5 × 5 +12
= 25 + 12
= 37
Explanation:
Place x = 5 in the given expression 5x + 12. First multiply 5 with 5 the product is 25. Add 25 to 12 the sum is 37.
Question 34.
20 – 2x =
Answer:
For x = 5
20 – 2x = 20 – 2 × 5
= 20 – 10
= 10
Explanation:
Place x = 5 in the given expression 20 – 2x. First multiply 2 with 5 the product is 10. Subtract 10 from the 20 the difference is 10.
Question 35.
\(\frac{x}{10}\) + 2 =
Answer:
For x = 5
x/10 + 2 = 5/10 + 2
= 1/2 + 2
= 0.5 + 2
2.5
Explanation:
Place x = 5 in the given expression x/10 + 2. First divide 5 by 10 the result is 1/2which is 0.5. Add 0.5 with 2 the sum is 2.5.
Question 36.
\(\frac{6 x}{5}\) + 12 =
Answer:
For x = 5
6x/5 + 12 = (6 × 5)/5 + 12
= 6 + 12
= 18
Explanation:
Place x = 5 in the given expression 6x/5 + 12. First multiply 6 with 5 the product is 30. Next divide 30 by 5 the result is 6. Add 6 with 12 the sum is 18.
Fill in the boxes with the correct expressions. In the last box on the right, evaluate each expression for m = 28.
Example

Question 37.

Answer:

For m= 28
3m + 5 = 3 × 28 + 5
= 84 + 5
= 89
Explanation:
In the above image we can observe four boxes. Multiply 3 with m the product is 3m. Next add 3m with 5 the sum is
3m + 5.
Place m = 28 in the expression 3m + 5. Multiply 3 with 28 the product is 84. Add 84 with 5 the sum is 89.
Question 38.
Answer:
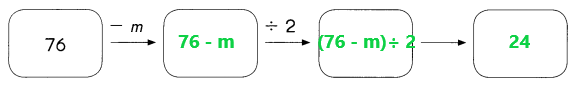
For m = 28
(76 – m) ÷ 2 = (76 – 28) ÷ 2
= 48 ÷ 2
= 24
Explanation:
In the above image we can observe four boxes. Subtract m from 76. Next divide 76 – m by 2.
Place m = 28 in the expression (76 – m) ÷ 2. Subtract 28 from 76 the difference is 48. Divide 48 by 2 the result is 24.
Question 39.
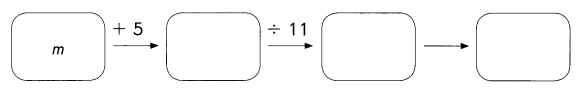
Answer:
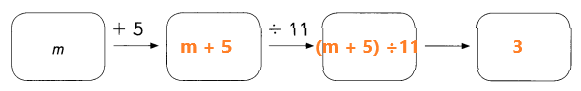
For m = 28
(m + 5) ÷ 11 = (28 + 5) ÷ 11
= 33 ÷ 11
= 3
Explanation:
In the above image we can observe four boxes. Add m to 5. Next divide m + 5 by 11.
Place m = 28 in the expression (m + 5) ÷ 11. Add 28 with 5 the sum is 33. Divide 33 by 11 the result is 3.
Question 40.
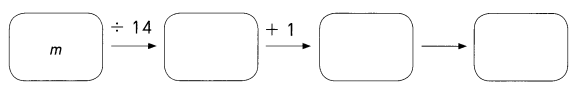
Answer:
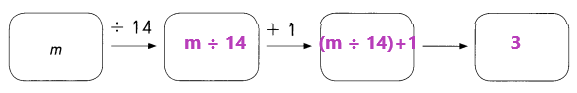
For m = 28
(m ÷ 14) + 1 = (28 ÷ 14) + 1
= 2 + 1
= 3
Explanation:
In the above image we can observe four boxes. Divide m by 14. Next add (m ÷ 14) with 1.
Place m = 28 in the expression (m ÷ 14) + 1. Divide 28 by 14 the result is 2. Add 2 with 1 the sum is 3.
Question 41.

Answer:

For m = 28
4m ÷ 16 = 4 × 28 ÷ 16
= 112 ÷ 16
= 7
Explanation:
In the above image we can observe four boxes. Multiply m with 4 the product is 4m. Next divide 4m by 16 the result is 4m ÷ 16.
Place m = 28 in the expression 4m ÷ 16. Multiply 4 with 28 the product is 112. Divide 112 by 16 the result is 7.
Evaluate each expression for z = 1,256.
Question 42.
41 z – 39
Answer:
For z = 1,256
41 z – 39 = 41 × 1,256 – 39
= 51,496 – 39
= 51,457
Explanation:
Place z = 1,256 in the given expression 41 z – 39. Multiply 41 with 1,256 the product is 51,496. Subtract 39 from 51,496 the difference is 51,457.
Question 43.
\(\frac{18,661-z}{5}\)
Answer:
For z = 1,256
(18,661 – z) ÷ 5 = (18,661 – 1,256) ÷ 5
= 17,405 ÷ 5
= 3,481
Explanation:
Place z = 1,256 in the given expression (18,661 – z) ÷ 5. Subtract 1,256 from 18,661 the difference is 17,405. Divide 17,405 by 5 the result is 3,481.
Question 44.
\(\frac{13 z}{8}\) + 7,389
Answer:
For z = 1,256
(13 z ÷ 8) + 7,389 = (13 × 1,256 ÷ 8) + 7,389
= (16,328 ÷ 8) + 7,389
= 2,041 + 7,389
= 9,430
Explanation:
Place z = 1,256 in the given expression (13 z ÷ 8) + 7,389. Multiply 13 with 1,256 the product is 16,328. Divide 16,328 by 8 the result is 2,041. Add 2,041 with 7,389 the sum is 9,430.
Question 45.
\(\frac{9 z-1,476}{42}\)
Answer:
For z = 1,256
(9z – 1,476) ÷ 42 = (9 × 1,256 – 1,476) ÷ 42
= (11,304 – 1,476) ÷ 42
= 9,828 ÷ 42
= 234
Explanation:
Place z = 1,256 in the given expression (9z – 1476) ÷ 42. Multiply 9 with 1,256 the product is 11,304. Subtract 1,476 from 11.304 the difference is 9,828. Divide 9,828 by 42 the result is 234.