Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 4 Review Test to score better marks in the exam.
Math in Focus Grade 7 Course 2 A Chapter 4 Review Test Answer Key
Concepts and Skills
Solve each equation.
Question 1.
8x – 7 = 17
Answer:
x = 3
Explanation:
Given, 8x – 7 = 17
Add 7 on both sides.
8x – 7 + 7 = 17 + 7
8x = 24
Divide 8 on both sides.
8x ÷ 8 = 24 ÷ 8
x = 3
Question 2.
4 – 6x = 8
Answer:
x = -(2/3)
Explanation:
Given, 4 – 6x = 8
Subtract 4 on both sides.
4 – 6x – 4 = 8 – 4
-6x = 4
Divide -6 on both sides.
-6x ÷ -6 = 4 ÷ -6
x = -(2/3)
Question 3.
6 – \(\frac{y}{3}\) = 0
Answer:
y = 18
Explanation:
Give, 6 – (y/3) = 0
Subtract 6 on both sides.
6 – (y/3) – 6= 0 – 6
-(y/3) = -6
(y/3) = 6
Multiply 3 on both sides.
(y/3) × 3 = 6 × 3
y = 18
Question 4.
3 – 3.6x = 4.2
Answer:
x = -0.333
Explanation:
Given, 3 – 3.6x = 4.2
Subtract 3 on both sides.
3 – 3.6x – 3 = 4.2 – 3
-3.6x = 1.2
Divide -3.6 on both sides.
-3.6x ÷ -3.6 = 1.2 ÷ -3.6
x = -0.333
Question 5.
7x – 5 = 3x + 4
Answer:
x = (3/2)
Explanation:
Given, 7x – 5 = 3x + 4
Add 5 on both sides.
7x – 5 + 5 = 3x + 4 + 5
7x = 3x + 9
Subtract 3x on both sides.
7x – 3x = 3x + 9 – 3x
4x = 9
Divide 4 on both sides.
4x ÷ 4 = 9 ÷ 4
x = (9/4)
x = (3/2)
Question 6.
\(\frac{7}{10}\)y – \(\frac{1}{5}\) = \(\frac{3}{5}\)y + \(\frac{6}{5}\)
Answer:
y = 14
Explanation:
(7/10)y – (1/5) = (3/5)y + (6/5)
Add (1/5) on the both sides.
(7/10)y – (1/5) + (1/5) = (3/5)y + (6/5) + (1/5)
(7/10)y = (3/5)y + (7/5)
Subtract (3/5)y on both sides.
(7/10)y – (3/5)y = (3/5)y +(7/5) – (3/5)y
(7/10)y – ((3×2)/10)y =(7/5)
(7/10)y – (6/10)y =(7/5)
(y/10) = (7/5)
Multiply 1y = 140 on both sides.
(y/10) × 10 = (7/5) × 10
y = 14
Question 7.
3.4y – 5.2 – 3y = 2
Answer:
y = 18
Explanation:
Given, 3.4y – 5.2 – 3y = 2
0.4y – 5.2 = 2
Add 5.2 on both sides.
0.4y – 5.2 + 5.2 = 2 + 5.2
0.4y = 7.2
Divide 0.4 on both sides.
0.4y ÷ 0.4 = 7.2 ÷ 0.4
y = 18
Question 8.
15y – 4(2y – 3) = -2
Answer:
y = -2
Explanation:
Given, 15y – 4(2y – 3) = -2
15y – 8y + 12 = -2
7y + 12 = -2
Subtract 12 on both sides.
7y + 12 – 12= -2 – 12
7y = -14
Divide 7 on both sides.
7y ÷ 7= -14 ÷ 7
y = -2
Question 9.
\(\frac{1}{4}\)(x + 3) + \(\frac{3}{8}\)x = \(\frac{13}{4}\)
Answer:
x = 4
Explanation:
Given, (1/4)(x + 3) + (3/8)x = (13/4)
(1/4)x + (3/4) + (3/8)x = (13/4)
Subtract (3/4) on both sides.
(1/4)x + (3/4) + (3/8)x – (3/4) = (13/4) – (3/4)
(1/4)x + (3/8)x =(13-3)/4
(2 + 3)x/8 = 10/4
(5/8)x = (10/4)
Multiply 8 on both sides.
(5/8)x × 8 = (10/4) × 8
5x = 20
Divide 5 on both sides.
5x ÷ 5 = 20 ÷ 5
x = 4
Question 10.
0.4(x + 0.7) = 0.6x – 4.2
Answer:
x = 22.4
Explanation:
Given, 0.4(x + 0.7) = 0.6x – 4.2
0.4x + 0.28 =0.6x – 4.2
Add 4.2 on the both sides.
0.4x +0.28 + 4.2 =0.6x – 4.2 + 4.2
0.4x + 4.48 = 0.6x
Subtract 0.4x on the both sides.
0.4x + 4.48 – 0.4x = 0.6x – 0.4x
4.48 = 0.2x
0.2x = 4.48
Divide o.2 on both sides.
0.2x ÷ 0.2 = 4.48 ÷ 0.2
x = 22.4
Solve each inequality. Graph each solution set.
Question 11.
4x – 3 > 1
Answer:
x > 1
Explanation:
Given, 4x – 3 > 1
Add 3 on both sides.
4x – 3 + 3 > 1 + 3
4x > 4
x > 1
Question 12.
6 ≤ 1 – 5x
Answer:
-1 ≤ x
Explanation:
Given, 6 ≤ 1 – 5x
Subtract 6 on both sides.
6 – 6 ≤ 1 – 5x – 6
0 ≤ -5x – 5
0 ≤ -5 (x + 1)
Divide -5 on both sides.
0 ÷ -5 ≤ -5 (x + 1) ÷ -5
0 ≤ (x + 1)
-1 ≤ x
Question 13.
\(\frac{2}{3}\) – \(\frac{x}{6}\) ≥ –\(\frac{1}{2}\)
Answer:
x ≤ 1
Explanation:
(2/3) – (x/6) ≥ (1/2)
Subtract (2/3) on both sides.
(2/3) – (x/6) – (2/3) ≥ (1/2) – (2/3)
-(x/6) ≥ (3 – 4/6)
-(x/6) ≥ -(1/6)
Multiply -6 on both sides.
-(x/6) × (-6) ≥ -(1/6) × (-6)
x ≤ 1
Question 14.
-6.9 < 8.1 – 1.5x
Answer:
x > 10
Explanation:
Given, -6.9 < 8.1 – 1.5x
Subtract 8.1 on both sides.
-6.9 – 8.1 < 8.1 – 1.5x – 8.1
-15 < -1.5x
1.5x > 15
Divide 1.5 on both sides.
1.5x ÷ 1.5 > 15 ÷ 1.5
x > 10
Question 15.
9y – 5 ≤ 4y + 15
Answer:
y ≤ 4
Explanation:
Given, 9y – 5 ≤ 4y + 15
Subtract 4y on both sides.
9y – 5 – 4y ≤ 4y + 15 – 4y
5y – 5 ≤ 15
Add 5 on both sides.
5y – 5 + 5 ≤ 15 + 5
5y ≤ 20
Divide 5 on both sides.
5y ÷ 5 ≤ 20 ÷ 5
y ≤ 4
Question 16.
\(\frac{7}{9}\)x – \(\frac{2}{3}\) > \(\frac{1}{6}\)x + 3
Answer:
x > 6
Explanation:
Given, (7/9)x – (2/3) > (1/6)x + 3
Subtract (1/6)x on both sides.
(7/9)x – (2/3) – (1/6)x > (1/6)x + 3 – (1/6)x
(14 – 3)/18x – (2/3) > 3
11/18x – (2/3) > 3
Add (2/3) on both sides.
11/18x- (2/3) + (2/3) > 3 + (2/3)
11/18x > (11/3)
Divide 11 on both sides.
11/18x ÷ 11 > (11/3) ÷ 11
(1/18)x > (1/3)
Multiply 3 on both sides.
(1/18)x × 3 > (1/3) × 3
(1/6)x > 1
Multiply 6 on both sides.
(1/6)x × 6 > 1 × 6
x > 6
Question 17.
12.9 < 0.3(5.3 – x)
Answer:
Question 18.
3(x + 1) > 5x + 7
Answer:
Question 19.
\(\frac{1}{5}\)(4x – 1) ≥ \(\frac{2}{3}\)x + \(\frac{3}{5}\)
Answer:
x ≥ 6
Explanation:
Given, (1/5)(4x – 1) ≥ (2/3)x + (3/5)
Multiply 5 on both sides
(1/5)(4x – 1) × 5 ≥ ((2/3)x + (3/5)) × 5
(4x – 1) ≥ (10/3)x + 3
Add 1 on both sides.
(4x – 1) + 1 ≥ (10/3)x + 3 + 1
4x ≥ (10/3)x + 4
Subtract (10/3)x on both sides.
4x – (10/3)x ≥ (10/3)x + 4 – (10/3)x
(12 – 10)x/3 ≥ 4
(2/3)x ≥ 4
Multiply 3 on both sides.
(2/3)x × 3 ≥ 4 × 3
2x ≥ 12
Divide 2 on both sides.
2x ÷ 2 ≥ 12 ÷ 2
x ≥ 6
Question 20.
4(3 – 0.1x) ≤ 15 – 0.6x
Answer:
x ≤ 15
Explanation:
Given, 4(3 – 0.1x) ≤ 15 – 0.6x
12 -0.4x ≤ 15 – 0.6x
Subtract 12 on both sides.
12 -0.4x – 12 ≤ 15 – 0.6x – 12
-0.4x ≤ 3 -0.6x
Add 0.6x on both sides.
-0.4x + 0.6x ≤ 3 -0.6x + 0.6x
0.2x ≤ 3
Divide 0.2 on both sides.
0.2x ÷ 0.2 ≤ 3 ÷ 0.2
x ≤ 15
Problem Solving
Write an equation for questions 21 to 25. Solve and show your work.
Question 21.
Aiden wrote a riddle: Five less than \(\frac{1}{5}\) times a number is the same as the sum of the number and \(\frac{1}{3}\). Find the number.
Answer:
x = -(20/3)
Explanation:
Let us consider the number be ‘x’.
(1/5)x – 5 = x + (1/3)
Add 5 on both sides.
(1/5)x – 5 + 5 = x + (1/3) + 5
(1/5)x = x + (16/3)
Subtract (1/5)x on both sides.
(1/5)x – (1/5)x = x + (16/3) – (1/5)x
0 = (4/5)x + (16/3)
(4/5)x = (- 16/3)
Multiply 5 on both sides.
(4/5)x × 5 = (- 16/3) × 5
4x = – 80/3
Divide 4 on both sides.
4x ÷ 4 = (- 80/3) ÷ 4
x = -(20/3)
Question 22.
Mary is 6 years older than her sister Kelly. The sum of their ages is 48. How old is Kelly?
Answer:
Kelly’s age, x = 21
Explanation:
Let us consider the age of the Kelly be ‘x’.
Age of Mary is x +6
Sum of their ages = 48
x +x + 6 = 48
2x + 6 = 48
Subtract 6 on both sides.
2x + 6 – 6 = 48 – 6
2x = 42
Divide 2 on both sides.
2x ÷ 2 = 42 ÷ 2
x = 21
Question 23.
The sum of the page numbers of two facing pages in a book is 145. What are the page numbers?
Answer:
x = 72; x + 1 = 73.
72, 73 are the page numbers.
Explanation:
Let us consider the numbers be x and x+1.
x + x +1 = 145
2x + 1 = 145
Subtract 1 on both sides.
2x + 1 – 1 = 145 – 1
2x = 144
Divide 2 on both sides.
2x ÷ 2 = 144 ÷ 2
x = 72
x + 1 = 73
The sum of numbers of two facing pages in a book = 145
Question 24.
The perimeter of an equilateral triangle is 6\(\frac{3}{4}\) inches. Find the length of each side of the equilateral triangle.
Answer:
Length of each side, a = (3/2)
Explanation:
Given, The perimeter of an equilateral triangle is 6(3/4).
3a = 6(3/4)
Divide 3 on both sides.
3a ÷ 3 = 6(3/4) ÷ 3
a = (6/4)
a = (3/2)
Question 25.
The sum of the interior angle measures of a quadrilateral is 360°. The measure of angle A is three times the measure of angle D. The measure of angle 6 is four times that of angle D. The measure of angle C is 24° more than angle B. Find the measure of each angle of the quadrilateral.
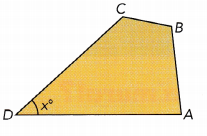
Answer:
Write an inequality for each question. Solve and show your work.
Question 26.
Laura wants the average amount of money she spends each day on her four-day vacation to be no more than $64. On the first three days, she spends $71, $62, and $59. What is the greatest amount of money she can spend on the fourth day?
Answer:
64
Explanation:
Given, Mean = ax=n(Mean)−(a1+...+an)
= 4(64) – (71 + 62 + 59)
= 256 – 192
= 64
Question 27.
Kevin plans to sign up for p hours of training at a culinary school. The school offers two payment options as shown below.

For how many hours of training is Option B less expensive than Option A?
Answer:
x < 20, 20 hours.
Explanation:
Let us consider number of hours be ‘x’.
18x + 0 < 8x +200
18x < 8x + 200
Subtract 8x on both sides.
18x – 8x < 8x + 200 – 8x
10x < 200
Divide 10 on both sides.
10x ÷ 10 < 200 ÷ 10
x < 20
Question 28.
Peter has found a job in a computer store. As shown below, he has two options for how he will be paid. The commission he makes for Option B is based on his weekly sales. For example, if his sales total $1,000 a week, he receives his base salary of $250 plus 8% of $1,000.

Peter is thinking about Option B. What would his weekly sales need to be for him to make at least as much as he would for Option A?
Answer:
The sales should be nearly above 4000$ per week to get more than Option A. Option A is better than Option B.
Explanation:
Let us consider ‘x’ be the number of sales.
600 ≥ 250 + 0.08x
Subtract 250 on both sides.
600 – 250 ≥ 250 + (0.08×1000)x – 250
350 ≥ 80x
Divide 80 on both sides.
350 ÷ 80 ≥ 80x ÷ 80
4 ≥ x
The sales should be nearly above 4000$ per week to get more than Option A.
so Option A is better than Option B.
Question 29.
The school events committee is planning to buy a banner and some helium balloons for graduation night. A store charges them $35 for the banner and $3.50 for each helium balloon. If the committee has at most $125 to spend, how many helium balloons can they buy?
Answer:
x ≤ 25
Explanation:
Let us consider number of helium balloons be ‘x’.
35 + 3.5x ≤ 125
Subtract 35 on both sides.
35 + 3.5x – 35 ≤ 125 – 35
3.5x ÷ 3.5 ≤ 90 ÷ 3.5
Divide 3.5 on both sides.
3.5x ≤ 90
x ≤ 25
Question 30.
The coach of the field hockey team can spend at most $475 on new team uniforms. The coach will order the uniforms online and pay a mailing cost of $6.50. If each uniform costs $29, how many uniforms can the coach order?
Answer:
x ≤ 16, 16 uniforms.
Explanation:
Let us consider the number of uniforms be ‘x’.
6.5 + 29x ≤ 475
Subtract 6.5 on both sides.
6.5 + 29x – 6.5 ≤ 475 – 6.5
29x ≤ 468.5
Divide 29 on both sides.
29x ÷ 29 ≤ 468.5 ÷ 29
x ≤ 16