Math in Focus Grade 6 Chapter 10 Lesson 10.4 Answer Key Area of Composite Figures

Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 10 Lesson 10.4 Area of Composite Figures to score better marks in the exam.

Math in Focus Grade 6 Course 1 B Chapter 10 Lesson 10.4 Answer Key Area of Composite Figures

Math in Focus Grade 6 Chapter 10 Lesson 10.4 Guided Practice Answer Key

Use graph paper. Copy the hexagon and solve.

Question 1.
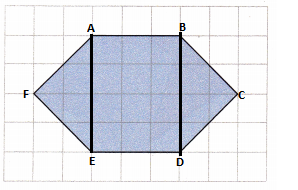
Divide the hexagon into two identical triangles and a rectangle.
Answer:

Explanation:
As shown in the figure, a regular hexagon is divided into two identical traingles and a rectangle.
The two identical traingle are AFE and BCD.
The rectangle formed is ABDE.

Question 2.
Divide the hexagon in another way. Name the polygons that make up the hexagon.

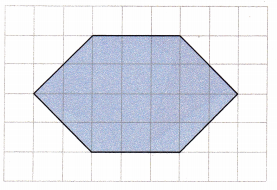
Answer:

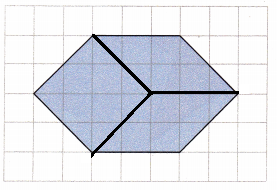
Explanation:
Mark the center of the hexagon.
Draw a line from the center point to a vertex.
Draw lines from the center point to the third and fifth vertices.
Each part is a rhombus, which is a four-sided figure with equal side lengths and two sets of parallel sides.
A hexagon can form 3 identical rhombus.

Complete.

Question 3.
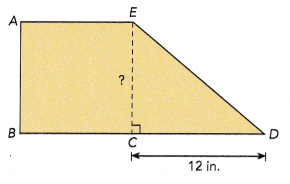
Trapezoid ABDE is made up of square A BCE and triangle ECD. triangle ECD is 60 square inches. The length of \(\overline{C D}\) is 12 inches.

a) Find the height of triangle ECD.

Area of triangle ECD = in.²
Area of triangle ECD = \(\frac{1}{2}\)bh
= \(\frac{1}{2}\) ∙ ∙ EC
= ∙ EC
÷ = ∙ EC ÷
= EC
The height of triangle ECO is î.. inches,
Answer:
In triangle ECD, the base length is equal to 12 in and the area is 60 sq.in.
Area of triangle ECD = \(\frac{1}{2}\)bh
60 = \(\frac{1}{2}\)×12×EC
60 = 6×EC
60÷6 = 6×EC÷6
10 = EC
The height of triangle ECD is 10 in.

b) Find the area of square ABCE.
Area of square ABCE = l²
=
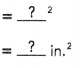
The area of square ABCE is  square inches.
Answer:
A square has all equal sides, so the length of it will be 10 in.
Area of square ABCE = length×length
= 10×10
= 100 sq.in
The area of square ABCE is 100 sq.in

c) Find the areà of trapezoid ABDE.
Area of the trapezoid ABDE
= area of square ABCE + area of triangle ECD
= +
=  in.²
The area of trapezoid ABDE is square inches.
Answer:
Area of the trapezoid ABDE
= \(\frac{1}{2}\)×(sum of bases)×height
Length of BD = BC+CD = 10+12 = 22 in
= \(\frac{1}{2}\)×(10+22)×10
= \(\frac{1}{2}\)×32×10
= 16×10
= 160 sq.in

Complete.

Question 4.
The area of parallelogram ABEF is 84 square meters.

a) Find the area of triangle BDE.
Area of parallelogram ABEF = bh
= ∙ h
÷ = h ÷
= h
The height of parallelogram ABEF is also the height of triangle BDE.
Area of triangle BDE = \(\frac{1}{2}\)bh
= \(\frac{1}{2}\) • BD • h
= \(\frac{1}{2}\) • ( + ) •
= m²
The area of triangle BDE is square meters.
Answer:
Given that area of parallelogram ABEF is 84 sq.m and base is 5m.
Area of parallelogram ABEF = bh
84 = 5×h
84÷5 = 5×h÷5
16.8 = h
The height of parallelogram ABEF is also the height of triangle BDE which is 16.8 m high.
Area of triangle BDE = \(\frac{1}{2}\)bh
= \(\frac{1}{2}\) × BD × h
= \(\frac{1}{2}\) × (BC+CD) × h
= \(\frac{1}{2}\) × (12+8) × h
= \(\frac{1}{2}\) × 20 × 16.8
= \(\frac{1}{2}\) × 336
= 168 sq.m

b) Find the area of trapezoid CDEF.
Parallelogram ABEF and trapezoid CDEF have the same height.
Area of trapezoid CDEF = \(\frac{1}{2}\)h(b₁ + b₂)
= • • ( + )
The area of trapezoid CDEF is square meters.
Answer:
Parallelogram ABEF and trapezoid CDEF have the same height. Therefore, the height will be 16.8 m
Since ABEF is a parallelogram, AB and FE will have the same length.
Height = 16.8 m
Sum of bases = 8+5 = 13
Area of trapezoid CDEF = \(\frac{1}{2}\)h(b₁ + b₂)
= \(\frac{1}{2}\)×16.8×13
= \(\frac{1}{2}\)×218.4
= 109.2 sq.m
The area of trapezoid CDEF is 109.2 sq.m.

Math in Focus Course 1B Practice 10.4 Answer Key

Copy each figure and draw straight lines to divide. Describe two ways to find the area of each figure.

Question 1.
Divide the figure into a rectangle and two right triangles.

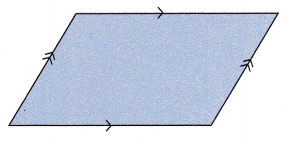
Answer:

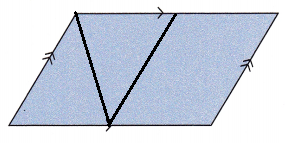
Divide the given figure into two equal parts.
It will form two identical rectangles.
Divide the first identical rectangle diagonally into two equal parts, which will form an equilateral triangle.

Question 2.
Divide the figure into a rectangle and two right triangles.

Answer:

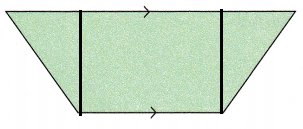
Explanation:
Draw a perpendicular segment between the base and the opposite vertex. Similarly, draw a line segment to the other end also.
The figure is divided now into three parts.
Two parts will form an right angle triangle and the third will form a rectangle.

Question 3.
Divide the figure into a rectangle and a right triangle.

Answer:

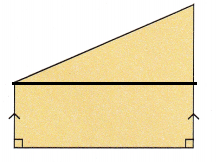
Explanation:
Draw a line segment parallel to the base length.
The first part formed is the right angle triangle and the second part is the rectangle.

Copy each figure and draw straight lines to divide. Describe a way to find the area.

Question 4.

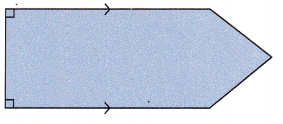
Answer:

Explanation:
If the given figure is divided using straight line, it will form a triangle and a rectangle.
Area of polygon will be the sum of areas of rectangle and area of triangle.
Area of polygon = Area of triangle+Area of rectangle
= (\(\frac{1}{2}\) × b × h) + (length×width)
Here, the base of triangle and the width of rectangle will be of same length.

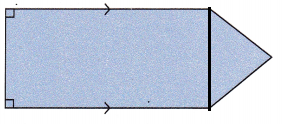
Question 5.

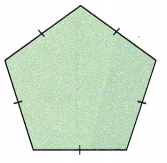
Answer:

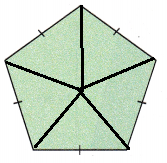
Explanation:
If the given figure is divided using straight line, it will form 5 identical triangles.
Area of polygon = n×\(\frac{1}{2}\)×b×h
Here n equals 5
Area of polygon = 5×\(\frac{1}{2}\)×b×h
Here, the base of trinagle will be equal to side length of the pentagon.

Find the area of each figure.

Question 6.
Parallelogram ABDE is made up of square ACDF, triangle ABC, and triangle FDE. Triangle ABC and triangle FDE are identical. The area of square ACDF is 36 square meters. Find the area of triangle ABC. Then find the area of parallelogram ABDE.

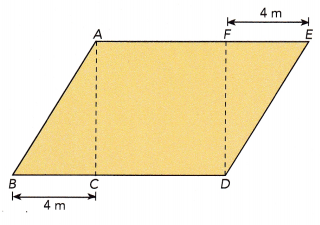
Answer:
Given that ACDF is a square and its area is 36 sq.m
Area of ACDF = side×side
36 = side×side
6×6 = side×side
Therefore, side of a sqaure will be 6 m.
Here, the side of square is equal to the height of the trinagle.
The height of triangle is 6m and the base is 4m.
Area of triangle = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×4×6
= 24÷2
= 12 sq.m
Area of triangle ABC and DFE will be same as both have the same dimensions.
Area of parallelogram ABDE = Area of ABC + Area of DFE + Area of ACDF
= 12+12+36
= 60 sq.m

Question 7.
Math Journal Describe how you would divide the figure with straight lines. Which sides of the figure would you measure to find its area? Explain your answer.

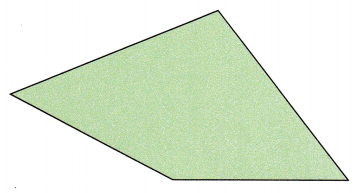
Answer:

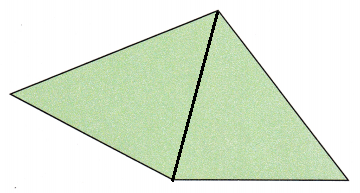
Explanation:
Draw a vertical line segment between the two vertex and divide it in two parts.
Two triangles will be formed. Since both the trinagles lie on same base, the base length of these triangles will be same. The perpendicular segment between the base and the opposite vertex will be the height of the triangle.
Measure the drawn line segment to get the base length and the perpendicular line segment to get the height.
Area of triangle can be found using the formula \(\frac{1}{2}\)×b×h.
Area of polygon will be the sum of areas of two trinagles formed.
Area of polygon = Area of first triangle + Area of second trinangle

Find the area of triangle EBC.

Question 8.
In the figure below, trapezoid ABDE is made up of three triangles, and figure ABCE is a parallelogram. Find the area of triangle EBC if the area of trapezoid ABDE is 180 square centimeters.

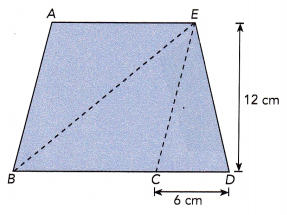
Answer:
Given that trapezoid ABDE is made up of three triangles, ABE BEC and ECD and its area is 180 sq.cm
Figure ABCE  is a parallelogram.
Area of triangle ECD:
In triangle ECD, the base measures 6cm and the height measures 12cm.
Area of ECD = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×6×12
= 72÷2
= 36 sq.cm
To find the area of triangle EBC, we need the length of BC, which is the base of the parallelogram ABCE.
To calculate the base of parallelogram ABCE , first we need to find the area of ABCE.
Area of trapezoid = Area of parallelogram ABCE + Area of triangle ECD
180 = Area of parallelogram ABCE + 36
180-36 = Area of parallelogram ABCE + 36 – 36
Area of parallelogram ABCE = 144 sq.cm
We know the height of the polygon is 12cm.
Area of parallelogram ABCE = base × height
144 = base × 12
144 ÷ 12 = (base × 12) ÷ 12
12 = base
Thus, the length of BC will be 12 cm.
Area of triangle EBC = \(\frac{1}{2}\)×b×h.
= \(\frac{1}{2}\)×12×12
= 144÷2
= 72 sq.cm

Solve. Use graph paper.

Question 9.
a) Plot the points P (-2, 2), Q (-2, -2), R (-4, -5), S (1, -5), and T (3, -2) on a coordinate plane. Connect the points in order to form figure PQRST.
Answer:
Plot the points P (-2, 2), Q (-2, -2), R (-4, -5), S (1, -5), and T (3, -2) on a coordinate plane.
When connected the points, it forms a polygon as shown below.

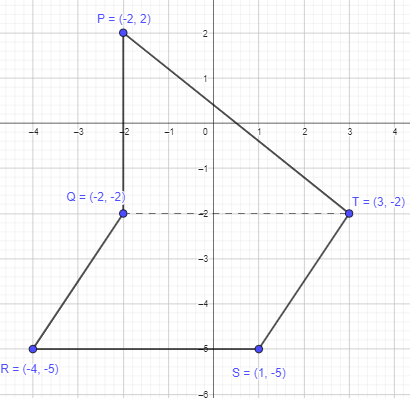
b) Find the area of figure PQRST.
Answer:
When the figure PQRST is divided using a line segment. It forms a triangle and a parallelogram.
Area of the polygon PQRST = Area of QTSR + Area of PQT
In the figure, QTSR forms a parallelogram. Let us assume RS as base and the perpendicular segment between the base and the opposite side will be the height.
Base = 5 units
Height = 3 units
Area of QTSR = base×height
= 5×3
= 15 sq.units
In the figure, PQT forms a parallelogram. Let us assume QT as base and the perpendicular segment between the base and the opposite vertex will be the height.
Base = 5 units
Height = 4 units
Area of PQT = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×5×4
= \(\frac{1}{2}\)×20
= 10 sq.units
Area of the polygon PQRST = 15 + 10
= 25 sq.units

c) Point V lies on along \(\overline{Q T}\). The area of triangle PQV is \(\frac{2}{5}\) the area of triangle PQT. Give the coordinates of point V. Plot point V on the coordinate plane.
Answer:
Given that the point V lies on along \(\overline{Q T}\). The area of triangle PQV is \(\frac{2}{5}\) the area of triangle PQT.
Area of PQV = \(\frac{2}{5}\)×area of triangle PQT
As calculated above, Area of PQT = 10 sq.units
= \(\frac{2}{5}\)×10
= 20÷5
= 4 sq.units
Let us assume PQ as base which is 5 units.
Area of PQV = \(\frac{1}{2}\)×b×h
4 = \(\frac{1}{2}\)×4×h
4 = 2×h
4÷2 = (2×h)÷2
2 = h
The height will be 2 units long.
Therefore the point V can be placed 2 units high from the base along \(\overline{Q T}\), which will be (0,-2)

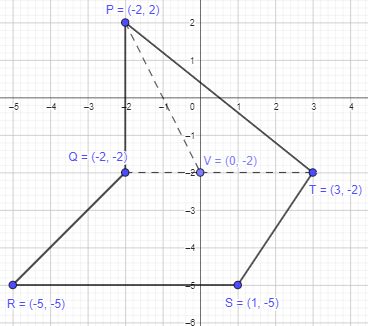
Find the area of trapezoid MNRS.

Question 10.
In the figure below, trapezoid MNRS is made up of trapezoid MNPT, triangle TPQ, and parallelogram TQRS. The area of triangle TPQ is 84 square feet. The lengths of \(\overline{N P}\), \(\overline{P Q}\), and \(\overline{Q R}\) are in the ratio 2 : 1.5 : 1.
Find the area of trapezoid MNRS.

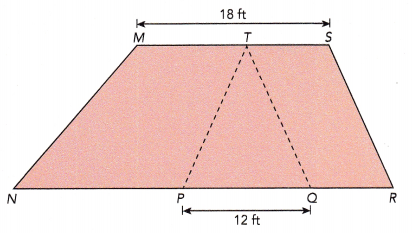
Answer:
Given that the trapezoid MNRS made up of trapezoid MNPT, triangle TPQ, and parallelogram TQRS.
Area of triangle TPQ = 84 sq.ft and the length of PQ is 12 ft and MS is 18 ft.
Area of TPQ = \(\frac{1}{2}\)×b×h, where b is length of PQ and h is unknown.
84 = \(\frac{1}{2}\)×12×h
84 = 6×h
84÷6 = (6×h)÷h
14 = h
The height of triangle will be 14 ft.
The lengths of \(\overline{N P}\), \(\overline{P Q}\), and \(\overline{Q R}\) are in the ratio 2 : 1.5 : 1
Let p be the proportion.
1.5p=12
1.5p÷1.5 = 12÷1.5
p = 8
Length of NP = 2p = 2×8 = 16 ft
Length of QR = 1p = 1×8 = 8 ft
NR = NP+PQ+QR
= 16+12+8
= 36 ft
In trapezoid MNRS, MS and NR will be the two parallel bases.
Area of trapezoid MNRS = \(\frac{1}{2}\)×(sum of bases)×height
= \(\frac{1}{2}\)×(18+36)×14
= \(\frac{1}{2}\)×54×14
= 756÷2
= 378 sq.ft
Thus, the area of trapezoid MNRS = 378 sq.ft

Find the area of triangle BDE.

Question 11.
The figure below is made up of two trapezoids ABEFand BCDE. The area of triangle FGE is 26 square inches, and the area of trapezoid BCDE is 82.5 square inches. BG is equal to GE. Find the area of triangle BDE.

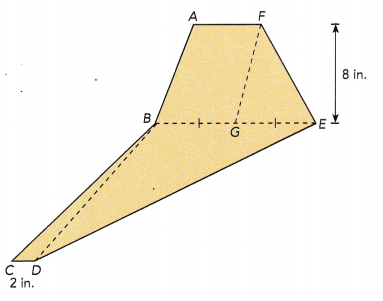
Answer:
The figure is made up of two trapezoids ABEFand BCDE, two triangles FGE,BCD and BDE.
Area of triangle FGE is 26 sq.in and height is 8 in.
Area of trapezoid BCDE is 82.5 sq.in
BG is equal to GE and length of CD is 2 in.
First we need to find the base length, GE.
Area of triangle FGE = \(\frac{1}{2}\)×base×height
26 = \(\frac{1}{2}\)×base×8
26 = 4×base
26÷4 = (4×base)÷4
6.5 = base
Length of GE = Length of BG = 6.5 in
Length of BE = Length of GE + Length of BG
= 6.5+6.5 =13 in
Area of trapezoid BCDE = \(\frac{1}{2}\)×(sum of bases)×height
82.5  =  \(\frac{1}{2}\)×(BE+CD)×height
82.5  =  \(\frac{1}{2}\)×15×height
82.5 = 7.5×height
82.5÷7.5 = (7.5×height)÷7.5
height = 11 in
The height of tarpezoid and triangle will be of same length.
Now, we can find the area of triangle BDE.
Area of triangle BDE = \(\frac{1}{2}\)×base×height
= \(\frac{1}{2}\)×BE×height
= \(\frac{1}{2}\)×BE×height
= \(\frac{1}{2}\)×13×11
= 143÷2
= 71.5 sq.in

Find the area of the shaded region.

Question 12.
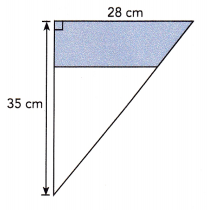
\(\frac{3}{8}\) of the triangle is shaded.

Answer:
Given trinagle is 28cm wide and 35cm high.
Area of trinagle = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × 28 × 35
= \(\frac{1}{2}\) × 980
= 980÷2
= 490 sq.cm
The shaded region is \(\frac{3}{8}\) of the triangle.
Therefore, area of shaded region will be \(\frac{3}{8}\) × 490
= 1470÷8
= 183.75 sq.cm

Find the height of trapezoid PQRS.

Question 13.
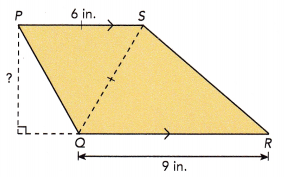
Trapezoid PORS s made up of isosceles triangle PQS and triangle SQR. The area of triangle PQS is 16.5 square inches. The areas of triangle PQS and triangle SQR are in the ratio 2 : 3, Find the height of trapezoid PQRS.

Answer:
Given that the trapezoid PORS s made up of isosceles triangle PQS and triangle SQR.
Area of triangle PQS is 16.5 square inches.
Since PQS is an isosceles triangle, PS will be equal to SQ.
The areas of triangle PQS and triangle SQR are in the ratio 2 : 3.
\(\frac{PQS}{SQR}\) = \(\frac{2}{3}\)
3×PQS = 2×SQR
3×16.5 = 2×SQR
49.5 = 2×SQR
49.5÷2 = (2×SQR)÷2
24.7 = SQR
Area of triangle SQR = 24.7 sq.in
Area of trapezoid = Area of triangle PQS + Area of triangle SQR
= 16.5+24.7
= 41.2 sq.in
Area of trapezoid = \(\frac{1}{2}\)×(sum of bases)×height
41.2 = \(\frac{1}{2}\)×(6+9)×height
41.2 = \(\frac{1}{2}\)× 15 ×height
41.2 = 7.5×height
41.2 ÷ 7.5 = (7.5×height)÷7.5
5.4= height
Thus, the height of trapezoid PQRS = 5.4 in

Find the area of each figure.

Question 14.
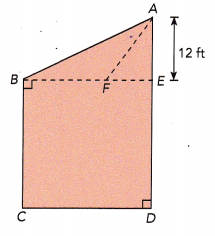
In the figure below, trapezoid ABCD is made up of square BCDE and triangles ABF and APE. The area of square BCDE is 576 square feet. The ratio of BF to FE is 2: 1. Find the area of triangle ABF.

Answer:
Given that the trapezoid ABCD is made up of square BCDE and triangles ABF and APE.
Area of square BCDE = 576 sq.ft
Area of square BCDE = length×length
576 = length×length
24×24 = length×length
Length of square = 24 ft.
The ratio of BF to FE is 2: 1.
\(\frac{BF}{FE}\) = \(\frac{2}{1}\)
1×BF = 2×FE
BE = 2×FE + FE
24 = 3×FE
24÷3 = 3×FE÷3
FE = 8ft
BF = 2×8 = 16ft
Area of triangle ABF = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × 16 × 12
= 192÷2
= 96 sq.ft

Brain @ Work

Question 1.
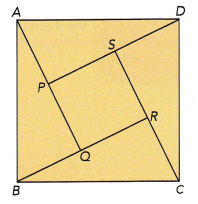
Figure ABCD is made up of square PQRS and four identical triangles. The area of triangle APD
is 49 square feet. The lengths of \(\overline{\mathrm{AP}}\) and \(\overline{\mathrm{PD}}\) are in the ratio 1: 2. Find the area of figure ABCD.

Answer:
Given that the figure ABCD is made up of square PQRS and four identical triangles. The area of triangle APD
is 49 square feet.
The lengths of \(\overline{\mathrm{AP}}\) and \(\overline{\mathrm{PD}}\) are in the ratio 1: 2.
Let the proportion be ‘p’
\(\frac{AP}{PD}\) = 1: 2
PD = 2×AP
Area of triangle APD = \(\frac{1}{2}\) × base × height
49 = \(\frac{1}{2}\) × PD × AP
49 = \(\frac{1}{2}\) × 2×AP×AP
49 = AP×AP
7×7 = AP×AP
AP = 7ft
PD = 2×7 = 14ft
As all are identical triangles, the longest side or base will be twice of the height.
SC = 2×DS, where DS = 7ft
PD = PS+SD
14 = PS+7
14-7 = PS+7-7
PS = 7ft
PQRS is a square, so all sides will be equal.
Area of square PQRS = length×length
= 7×7
= 49 sq.ft
Area of ABCD = Area of four identical triangles + Area of square PQRS
= 4×49 + 49
= 196+49
= 245 sq.ft

Question 2.
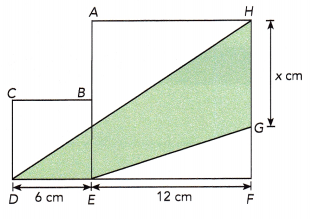
The figure is made up of squares BCDE and AEFH. The length of \(\overline{D E}\) is 6 centimeters, and the length of \(\overline{E F}\) is 12 centimeters.
a) Write the length of \(\overline{F G}\) in terms of x.
Answer:
Length of DE = 6 cm
Length of EF = 12 cm
Since AEFH is a square, all sides will be equal.
Therefore, the length of HF will be 12cm
HF = HG + GF
12 = x+GF
12-x = x+GF-x
GF = 12-x
Therefore, the length of \(\overline{F G}\) will be 12-x

b) Find the area of the shaded region in terms of x.
Answer:

c) Give the value of x for which the shaded region has the greatest area. What is the shape of the shaded region for the value of x you have given?

Answer:

Question 3.
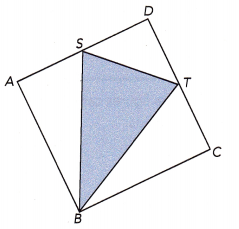
Figure ABCD is a square. Point S is in the middle of \(\overline{A D}\), and point T is in the middle of and \(\overline{C D}\). What fraction of the square is shaded?

Answer:
Given that the figure ABCD is a square.
Point S is in the middle of \(\overline{A D}\), and point T is in the middle of and \(\overline{C D}\).
To find the fraction of shaded square we need to find the area of trinagle STB.
Let us assume each side length of the square as 1m.
AD=DC=CB=BA=1m
Since S and T are the midpoints of AD and DC.
Length of DS = Length of SA = \(\frac{1}{2}\) m
Length of DT = Length of TC = \(\frac{1}{2}\) m
ASB forms a right angle triangle; AB²+AS² = SB²
1²+(\(\frac{1}{2}\))² = SB²
1+\(\frac{1}{4}\) = SB²
\(\frac{5}{4}\) = SB²
SB = √\(\frac{5}{4}\)
SB = \(\frac{√5}{2}\)
In triangle DST
ST²=(\(\frac{1}{2}\))² + (\(\frac{1}{2}\))²
= \(\frac{1}{4}\) + \(\frac{1}{4}\)
= \(\frac{2}{4}\)
= \(\frac{1}{2}\)
ST = √\(\frac{1}{2}\)
Draw a perpendicular segment from BU on ST

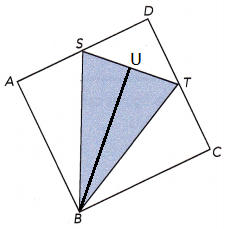
Now BUS will be a right angle triangle,
BS²=BU²+US²
Length of SU will be \(\frac{1}{2}\) of ST
Length of SU = \(\frac{1}{2}\) × \(\frac{1}{√2}\) = \(\frac{1}{2√2}\)
(\(\frac{√5}{2}\))² = BU²+ (\(\frac{1}{2√2}\) )²
\(\frac{5}{4}\) = BU²+\(\frac{1}{8}\)
\(\frac{5}{4}\)–\(\frac{1}{8}\) = BU²
(\(\frac{5}{4}\)×\(\frac{2}{2}\))-\(\frac{1}{8}\) = BU²
\(\frac{10}{8}\)–\(\frac{1}{8}\) = BU²
\(\frac{9}{8}\)= BU²
BU=√\(\frac{9}{8}\)
BU=\(\frac{3}{2√2}\)
Area of STB:
Length of ST=\(\frac{1}{√2}\)
Height = \(\frac{3}{2√2}\)
Area of triangle STB=\(\frac{1}{2}\)×b×h
=\(\frac{1}{2}\)×\(\frac{1}{√2}\)×\(\frac{3}{2√2}\)
= 2×√2×2√2
= 2×2×2=8(√2×√2=2)
= \(\frac{3}{8}\) sq.m