Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 4 Practice 2 Real-World Problems: Multiplying with Proper Fractions to finish your assignments.
Math in Focus Grade 5 Chapter 4 Practice 2 Answer Key Real-World Problems: Multiplying with Proper Fractions
Solve. Draw models to help you.
Question 1.
Lena has some eggs in the refrigerator. She takes out \(\frac{3}{5}\) of the eggs to make waffles and scrambled eggs. She uses \(\frac{2}{3}\) of the eggs she took out to make waffles. What fraction of the total number of eggs does Lena use to make waffles?
Answer:
\(\frac{2}{5}\)
Explanation:
Lena has some eggs in the refrigerator.
She takes out \(\frac{3}{5}\) of the eggs to make waffles and scrambled eggs.
She uses \(\frac{2}{3}\) of the eggs she took out to make waffles.
\(\frac{3}{5}\) x \(\frac{2}{3}\)
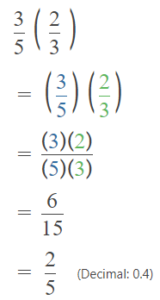
\(\frac{2}{5}\) of the total number of eggs that Lena use to make waffles
Question 2.
Dawn has \(\frac{5}{6}\) yard of lace. She uses \(\frac{4}{5}\) of it for a dress and the rest for a jewel box. How much lace does she use for the jewel box?
Answer:
\(\frac{1}{6}\) Lace use for the jewel box
Explanation:
\(\frac{4}{5}\) x \(\frac{5}{6}\) = \(\frac{20}{30}\) = \(\frac{2}{3}\)
\(\frac{5}{6}\) – \(\frac{2}{3}\) = \(\frac{5-4}{6}\) = \(\frac{1}{6}\)
Solve. Show your work.
Question 3.
Tasha finished a job in \(\frac{3}{4}\) hour. Megan finished it in of the time Tasha took. How long did Megan take to finish the job?
Answer:
45 minutes
Explanation:
Tasha finished a job in \(\frac{3}{4}\) hour.
Megan finished it in of the time Tasha took.
\(\frac{3}{4}\) x 60 = 45 minutes
45 minutes Megan take to finish the job
Question 4.
Lily has a bottle containing \(\frac{7}{8}\) quart of milk. She pours \(\frac{4}{5}\) of it into a bowl. What amount of milk does she pour into the bowl?
Answer:
\(\frac{7}{10}\)
Explanation:
Lily has a bottle containing \(\frac{7}{8}\) quart of milk.
She pours \(\frac{4}{5}\) of it into a bowl.
\(\frac{7}{8}\) x \(\frac{4}{5}\)
= \(\frac{28}{40}\)
= \(\frac{7}{10}\)
\(\frac{7}{10}\) amount of milk that she pour into the bowl
Question 5.
Raoul ran \(\frac{3}{4}\) mile in a race. Eduardo ran \(\frac{2}{7}\) of the distance that Raoul ran. What distance did Eduardo run?
Answer:
\(\frac{3}{14}\)
Explanation:
Raoul ran \(\frac{3}{4}\) mile in a race.
Eduardo ran \(\frac{2}{7}\) of the distance that Raoul ran.
\(\frac{3}{4}\) x \(\frac{2}{7}\)
= \(\frac{6}{28}\)
= \(\frac{3}{14}\)
\(\frac{3}{14}\) that Eduardo run
Solve. Draw models to help you.
Question 6.
Jenny spends \(\frac{1}{6}\) of her paycheck and saves \(\frac{2}{5}\) of the remaining amount. What fraction of her total paycheck is saved?
Answer:
\(\frac{1}{3}\)
Explanation
Jenny spends \(\frac{1}{6}\) of her paycheck
and saves \(\frac{2}{5}\) of the remaining amount.
x – \(\frac{1}{6}\)x
= \(\frac{5x}{6}\) pennies
\(\frac{5x}{6}\) x \(\frac{2}{5}\)
x = \(\frac{10}{30}\)
= \(\frac{1}{3}\)
\(\frac{1}{3}\) of her total paycheck is saved
Question 7.
In Rod’s family, \(\frac{3}{4}\) of the members wear glasses. Of those who do not wear glasses, \(\frac{1}{3}\) are male. What fraction of the family are males who do not wear glasses?
Answer:
\(\frac{1}{12}\)
Explanation:
In Rod’s family, \(\frac{3}{4}\) of the members wear glasses.
Of those who do not wear glasses, \(\frac{1}{3}\) are male.
x – \(\frac{3}{4}\)x
= \(\frac{4x-3x}{4}\)
= \(\frac{1}{4}\)x
x = \(\frac{1}{4}\) not wear glass
\(\frac{1}{4}\) x \(\frac{1}{3}\)
= \(\frac{1}{12}\)
\(\frac{1}{12}\) fraction of the family are males that not wear glasses
Solve. Draw models to help you.
Question 8.
Ned folded a set of origami figures. Of this set, \(\frac{5}{8}\) are cranes and \(\frac{1}{6}\) of the remainder are frogs. The rest are grasshoppers. What fraction of the origami figures are grasshoppers?
Answer:
\(\frac{11}{16}\)
Explanation:
Ned folded a set of origami figures. Of this set, \(\frac{5}{8}\) are cranes
and \(\frac{1}{6}\) of the remainder are frogs. The rest are grasshoppers.
\(\frac{5}{8}\) are cranes
\(\frac{3}{8}\) are not cranes
\(\frac{1}{6}\) x \(\frac{3}{8}\) = \(\frac{3}{48}\) = \(\frac{1}{16}\)
Let us convert
\(\frac{5}{8}\) as \(\frac{10}{16}\)
\(\frac{10}{16}\) + \(\frac{1}{16}\)
= \(\frac{11}{16}\)
\(\frac{11}{16}\) fraction of the origami figures are grasshoppers
Solve. Show your work
Question 9.
In a garden, \(\frac{2}{3}\) of the flowers are roses. Of the roses in the garden, \(\frac{5}{12}\) are yellow and the rest are red. What fraction of the flowers are red roses?
Answer:
\(\frac{1}{9}\)
Explanation:
In a garden, \(\frac{2}{3}\) of the flowers are roses.
Of the roses in the garden, \(\frac{5}{12}\) are yellow and the rest are red.
Roses = \(\frac{2}{3}\)
Yellow = \(\frac{5}{12}\) x \(\frac{2}{3}\)
= \(\frac{10}{36}\)
= \(\frac{5}{18}\)
Red = \(\frac{2}{3}\) – \(\frac{5}{18}\)
= \(\frac{36-30}{54}\)
= \(\frac{1}{9}\)
\(\frac{1}{9}\) fraction of the flowers are red roses
Question 10.
Karen collects local and foreign coins. Of the coins in her collection, \(\frac{1}{4}\) are foreign coins. Of the foreign coins, \(\frac{2}{5}\) are from Mexico. What fraction of the collection are foreign coins that are not from Mexico?
Answer:
\(\frac{3}{20}\) fraction of the collection are foreign coins that are not from Mexico
Explanation:
\(\frac{1}{4}\) are foreign coins
\(\frac{2}{5}\) x \(\frac{1}{4}\)
Mexico = \(\frac{1}{10}\)
Non Mexican
= \(\frac{1}{4}\) – \(\frac{1}{10}\)
= \(\frac{5-2}{20}\)
= \(\frac{3}{20}\)