This handy Math in Focus Grade 7 Workbook Answer Key Chapter 9 Lesson 9.4 Understanding Random Sampling Methods detailed solutions for the textbook questions.
Math in Focus Grade 7 Course 2 B Chapter 9 Lesson 9.4 Answer Key Understanding Random Sampling Methods
Hands-On Activity
Materials:
- list of names of 40 students
- a random number table
EXPLORE HOW A RANDOM SAMPLING PROCESS AFFECTS DATA COLLECTION
Work in groups of four or five.
STEP 1: Choose 40 students to participate in this activity. They will be asked how long it took them to get to school today.
STEP 2: Assign each of the 40 students a 2-digit number from 01 to 40.
STEP 3: Use the random number table to pick five 2-digit numbers. Discard any 2-digit numbers greater than 40.
![]()
STEP 4: Ask the 5 students whose numbers match those you picked in STEP 3 the following question and record the results. About how many minutes did it take you to commute to school today?
STEP 5: Find the mean and the mean absolute deviation of the data you collected in STEP 4.
STEP 6: Repeat STEP 3 to STEP 5 to generate new random samples, and to collect and analyze the data from each sample.
Math Journal Does the mean number of minutes vary greatly from sample to sample? Does the mean absolute deviation vary greatly from sample to sample? What are some problems you encountered in the random sampling process? Describe.
Answer:
We got by adding those two-digit numers:
Mean=sum of observations/number of observations.
Mean=4+18+19+27+37/5
Mean=105/5
Mean=21
Now calculate the Mean absolute deviation.
First, subtract the data set values from the mean
|4-21|=17
|18-21|=3
|19-21|=2
|27-21|=6
|37-21|=16
MAD=17+3+2+6+16/5
MAD=44/5
MAD=8.8
Mean varies greatly from sample to sample. comparing to mean MAD varies less.
It is easy to get the data wrong just as it is easy to get right.
The application of random sampling is only effective when all potential respondents are included within the large sampling frame. Everyone or everything that is within the demographic or group being analyzed must be included for the random sampling to be accurate. If the sampling frame is exclusionary, even in a way that is unintended, then the effectiveness of the data can be called into question and the results can no longer be generalized to the larger group.
Hands-On Activity
Materials:
- computer
- relevant books
COMPARE THE STRENGTHS AND WEAKNESSES OF RANDOM SAMPLING METHODS
Work in pairs.
Back ground
Every sampling method has its own strengths and weaknesses. Each method is designed for specific purposes. Sometimes you may find more than one method can be used in a particular situation. At another time, you may find it necessary to combine two methods to obtain the best possible random sample.
Be creative when you apply a random sampling method!
STEP 1: Research the strengths and weaknesses of the three random sampling methods.
STEP 2: Compile the information in a table shown below.
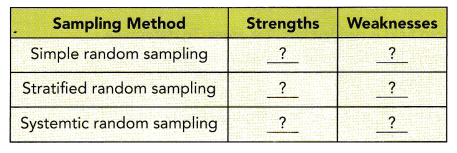
Math Journal Do you find that a weakness of one method can be addressed by another method? Explain.
Answer:
strengths of stratified:
– Has greater ability to make inferences within a stratum and comparisons across strata.
– Has slightly smaller random sampling errors for samples of the same sample size, thereby requiring smaller sample sizes for the same margin of error
– Obtains a more representative sample because it ensures that elements from each stratum are represented in the sample.
Weaknesses:
– Requires information on the proportion of the total population that belongs to each stratum
– Information on stratification variables is required for each element in the population. If such information is not readily available, it may be costly to compile.
– More expensive, time-consuming, and complicated than simple random sampling.
Simple random sampling:
Compared to other probability sampling procedures, simple random sampling has several strengths that should be considered in choosing the type of probability sample design to use Some of these include:
• Advanced auxiliary information on the elements in the population is not required. Such information is required for other probability sampling procedures, such as stratified sampling.
• Each selection is independent of other selections, and every possible combination of sampling units has an equal and independent chance of being selected. In systematic sampling, the chances of being selected are not independent of each other.
• It is generally easier than other probability sampling procedures (such as multistage cluster sampling) to understand and communicate to others.
• Statistical procedures required to analyze data and compute errors are easier than those required of other probability sampling procedures.
On the other hand, simple random sampling has important weaknesses. Compared to other probability sampling procedures, simple random samplings have the following weaknesses:
• A sampling frame of elements in the target population is required. An appropriate sampling frame may not exist for the population that is targeted, and it may not be feasible or practical to construct one. Alternative sampling procedures, such as cluster sampling, do not require a sampling frame of the elements of the target population.
• Simple random sampling tends to have larger sampling errors and less precision than stratified samples of the same sample size. Respondents may be widely dispersed; hence, data collection costs might be higher than those for other probability sample designs such as cluster sampling.
• Simple random sampling may not yield sufficient numbers of elements in small subgroups. This would not make simple random sampling a good choice for studies requiring comparative analysis of small categories of the population with much larger categories of the population
Strengths of systematic random sampling:
1. If the selection process is manual, systematic sampling is easier, simpler, less time-consuming, and more economical.
2. The target population need not be numbered and a sampling frame compiled if there is a physical representation.
3. If the ordering of the elements in the sampling frame is randomized, systematic sampling may yield results similar to simple random sampling.
Weaknesses:
1. If the sampling interval is related to the periodic ordering of the elements in the sampling frame, increased variability may result.
2. Combinations of elements have different probabilities of being selected.
3. Technically, only the selection of the first element is a probability selection since for subsequent selections, there will be elements of the target population that will have a zero chance of being selected.
Math in Focus Grade 7 Chapter 9 Lesson 9.4 Guided Practice Answer Key
Determine which sampling method is best suited for each situation.
Question 1.
Describe how you would carry out the sampling process. You may use a combination of methods, if you see fIt. Justify your process.
Scenario 1
A truck load of 3OOO oranges were delivered to a wholesale market. You are allowed to check 1% of the oranges as a random sample before deciding whether to accept the shipment.
Scenario 2
A grocer would like to find what items the store should carry to attract more customers. The grocer wants to survey loo people in the neighbourhood.
Answer:
Scenario 1: Systematic random sampling: Scenario 1 uses random sampling because you want the sample to cover a wide range of oranges in the shipment.
Scenario 2: Simple random sampling: Scenario 2 uses simple random sampling because it is just an opinion poll of people in the neighbourhood.
Math in Focus Course 2B Practice 9.5 Answer Key
Answer the following.
Question 1.
Explain what a random sampling process is.
Answer:
Random sampling is a method of choosing a sample of observations from a population to make assumptions about the population. It is also called probability sampling. The counterpart of this sampling is Non-probability sampling or Non-random sampling. The primary types of this sampling are simple random sampling, stratified sampling, cluster sampling, and multistage sampling. In the sampling methods, samples that are not arbitrary are typically called convenience samples.
The primary feature of probability sampling is that the choice of observations must occur in a ‘random’ way such that they do not differ in any significant way from observations, which are not sampled. We assume here that statistical experiments contain data that is gathered through random sampling.
Question 2.
Give an example of how a random sampling process is used in a real-world situation.
Answer:
– At a birthday party, teams for a game are chosen by putting everyone’s name into a jar, and then choosing the names at random for each team.
– On an assembly line, each employee is assigned a random number using computer software. The same software is used periodically to choose a number of the employees to be observed to ensure they are employing best practices.
– A restaurant leaves a fishbowl on the counter for diners to drop their business cards. Once a month, a business card is pulled out to award one lucky diner with a free meal.
– At a bingo game, balls with every possible number are placed inside a mechanical cage. The caller rotates the cage, tumbling around the balls inside. Then, she selects one of the balls at random to be called, like B-12 or O-65.
– A pharmaceutical company wants to test the effectiveness of a new drug. Volunteers are assigned randomly to one of two groups. The first group will receive the new drug; the second group will receive a placebo.
Question 3.
Why do people want to use random samples to collect information about a population?
Answer:
Random sampling offers two primary advantages. Because individuals who make up the subset of the larger group are chosen at random, each individual in the large population set has the same probability of being selected. This creates, in most cases, a balanced subset that carries the greatest potential for representing the larger group as a whole.
Moreover, they want to collect information to understand the characteristics of the population.
Question 4.
Explain why a biased sample is not an appropriate sample.
Answer:
Sampling bias occurs when some members of a population are systematically more likely to be selected in a sample than others. It is also called ascertainment bias in medical fields. Sampling bias limits the generalizability of findings because it is a threat to external validity, specifically population validity. In other words, findings from biased samples can only be generalized to populations that share characteristics with the sample.
State which sampling method is being described.
Question 5.
A frozen yogurt store sells 5 flavors: vanilla, chocolate, strawberry, macadamia nut, and peppermint. To check the quality of the frozen yogurt, 5 tubs of each flavor were sampled.

Answer: Stratified random sampling.
Definition: In this sampling method, a population is divided into subgroups to obtain a simple random sample from each group and complete the sampling process (for example, number of girls in a class of 50 strength). These small groups are called strata. The small group is created based on a few features in the population. After dividing the population into smaller groups, the researcher randomly selects the sample.
Question 6.
A group of students conducted an online poll of Internet users by randomly selecting 500 Internet users.
Answer: Clustered sampling
Definition:
Cluster sampling is similar to stratified sampling, besides the population is divided into a large number of subgroups (for example, hundreds of thousands of strata or subgroups). After that, some of these subgroups are chosen at random and simple random samples are then gathered within these subgroups. These subgroups are known as clusters. It is basically utilised to lessen the cost of data compilation.
Question 7.
To check the freshness of the bagels at a bakery, the baker randomly picked 5 bagels at an interval of every hour.
Answer: Systematic random sampling
In this method, the items are chosen from the destination population by choosing the random selecting point and picking the other methods after a fixed sample period. It is equal to the ratio of the total population size and the required population size.
Question 8.
Unique numbers were assigned to the members of a country club. The club manager used a random number generator to choose 150 numbers that were matched to members of the club.
Answer: Stratified random sampling.
In this sampling method, a population is divided into subgroups to obtain a simple random sample from each group and complete the sampling process (for example, number of girls in a class of 50 strength). These small groups are called strata. The small group is created based on a few features in the population. After dividing the population into smaller groups, the researcher randomly selects the sample.
Question 9.
Out of 100 students, the teachers randomly choose the first student and every sixth student thereafter.
Answer: Systematic random sampling
In this method, the items are chosen from the destination population by choosing the random selecting point and picking the other methods after a fixed sample period. It is equal to the ratio of the total population size and the required population size.
Question 10.
To assess pollution levels in a region, water samples are taken from 5 rivers and 2 lakes for analysis.
Answer: Stratified random sampling.
In this sampling method, a population is divided into subgroups to obtain a simple random sample from each group and complete the sampling process (for example, number of girls in a class of 50 strength). These small groups are called strata. The small group is created based on a few features in the population. After dividing the population into smaller groups, the researcher randomly selects the sample.
Refer to the situation to answer the following.
Question 11.
Math Journal A corn field is divided into five areas. To determine whether the corn plants are healthy, you are asked to collect a random sample of 100 ears of corn for analysis.
a) If you use a stratified random sampling method, describe how you will go about collecting the random sample.
Answer:
In this sampling method, a population is divided into subgroups to obtain a simple random sample from each group and complete the sampling process (for example, number of girls in a class of 50 strength). These small groups are called strata. The small group is created based on a few features in the population. After dividing the population into smaller groups, the researcher randomly selects the sample.
according to the definition, we can write:
The 5 areas of the cornfield constitute 5 groups of corn plants. 20 ears of corn are randomly selected from each group.
b) Explain why the stratified random sampling method is preferred.
Answer:
It gives a fair representation of each of the five areas that’s why the stratified random sampling method is preferred.
Question 12.
Math Journal Explain why the simple sampling method may not give you a representative sample.
Answer:
When a sample is not representative, we will have a sampling error known as the margin of error. If we want to have a representative sample of 100 employees, we must choose a similar number of men and women. For example, if we have a sample inclined to a specific genre, then we will have an error in the sample.
The sample size is essential, but it does not guarantee that it accurately represents the population that we need. More than size, representativeness is related to the sampling frame, that is, to the list from which people are selected, for example, part of a survey. Therefore, we must take care that people from our target audience are included in that list to say that it is a representative sample.
Refer to the situation below to answer the following.
2,000 runners participated in a marathon. You want to randomly choose 60 of the runners to find out how long ¡t took each one to run the race.
Question 13.
Describe how you would select the 60 runners if you use a simple random sampling method.
Answer:
In this sampling method, each item in the population has an equal and likely possibility of getting selected in the sample (for example, each member in a group is marked with a specific number). Since the selection of item completely depends on the possibility, therefore this method is called the “Method of chance Selection”. Also, the sample size is large, and the item is selected randomly. Thus it is known as “Representative Sampling”.
According to the definition:
Pick runners randomly in the marathon to interview until 60 runners have been interviewed.
Question 14.
Describe how you would select the 60 runners if you use a systematic random sampling method.
Answer:
In this method, the items are chosen from the destination population by choosing the random selecting point and picking the other methods after a fixed sample period. It is equal to the ratio of the total population size and the required population size.
according to the definition:
Picking a few numbers out of a hat, but you can use any number of runners as long as you have a minimum size.
Question 15.
Describe how you would select the 60 runners if you use the stratified random sampling method.
Answer:
In this sampling method, a population is divided into subgroups to obtain a simple random sample from each group and complete the sampling process (for example, number of girls in a class of 50 strength). These small groups are called strata. The small group is created based on a few features in the population. After dividing the population into smaller groups, the researcher randomly selects the sample.
According to the definition:
Use age bands, for example, select randomly 15 runners from each of the 4 age bands. Below 20, 20 to 30, 30 to 40, and above 40.
Refer to the situation below to answer the following.
There are 1,650 trees growing in 5 areas within a park. The trees are numbered from 1 to 1,650. A systematic random sample of 40 trees is needed to check whether there are fungi causing root rot among the trees.
Question 16.
Describe how you would carry out a systematic random sampling.
Answer:
In this method, the items are chosen from the destination population by choosing the random selecting point and picking the other methods after a fixed sample period. It is equal to the ratio of the total population size and the required population size.
According to the definition:
Out of 1,650 trees, the researchers randomly choose the first tree and every sixth tree thereafter. Likewise, they select the fixed sample tree and check the trees if they are fungi causing root among the trees.
Question 17.
Describe how you would carry out a stratified random sampling.
Answer:
In this sampling method, a population is divided into subgroups to obtain a simple random sample from each group and complete the sampling process (for example, number of girls in a class of 50 strength). These small groups are called strata. The small group is created based on a few features in the population. After dividing the population into smaller groups, the researcher randomly selects the sample.
According to the definition:
Use the 5 areas of 5 groups of trees in the park and randomly select 8 trees within each area.
Refer to the situation below to answer the following.
Question 18.
A poll is taken in a small town to find out which candidate voters will choose in an election. A stratified sampling method is used to generate a random sample of 500 residents. The table shows the town population and the sample size within each group.
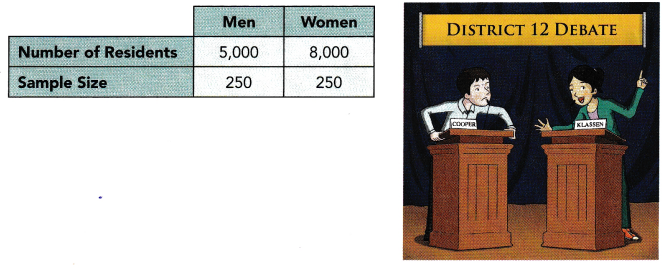
a) The stratified random sample has been criticized for not being representative of the population. What could possibly be the problem with the random sample?
Answer:
In the stratified random sampling method, we divide the groups into subgroups but in the representative the sample size is large, and the item is selected randomly. Moreover, the problem with the random sample is below:
1. No additional knowledge is taken into consideration.
Here a number of residents are more: 5000-men; 8000 women. From this, we need to select 500 residents in total.
Although random sampling removes an unconscious bias that exists, it does not remove an intentional bias from the process. Researchers can choose regions for random sampling where they believe specific results can be obtained to support their own personal bias. No additional knowledge is given consideration from the random sampling, but the additional knowledge offered by the researcher gathering the data is not always removed.
2. It is a complex and time-consuming method of research. With random sampling, every person or thing must be individually interviewed or reviewed so that the data can be properly collected. When individuals are in groups, their answers tend to be influenced by the answers of others. This means a researcher must work with every individual on a 1-on-1 basis. This requires more resources, reduces efficiencies, and takes more time than other research methods when it is done correctly.
b) How would you improve the above stratified random sampling?
Answer:
1. Stratified Random Sampling provides better precision as it takes the samples proportional to the random population.
2. Stratified Random Sampling helps minimize the biasness in selecting the samples.
3. Stratified Random Sampling ensures that no section of the population is underrepresented or overrepresented.
4. As this method provides greater precision, a greater level of accuracy can be achieved even by using a small size of samples. This saves resources.