Math in Focus Grade 5 Mid-Year Review Answer Key

Go through the Math in Focus Grade 5 Workbook Answer Key Mid Year Review to finish your assignments.

Math in Focus Grade 5 Mid-Year Review Answer Key

Test Prep

Multiple Choice
Fill in the circle next to the correct answer.

Question 1.
Which of the following is 3,450,026 in word form? (Lesson 1.1)
(A) Three million, four hundred fifty thousand, twenty-six
(B) Three million, four hundred thousand fifty, twenty-six
(C) Three million, fifty thousand four hundred, twenty-six
(D) Three million, forty-five thousand, twenty-six
Answer:
Option A is the correct answer

Question 2.
Which number is greatest? (Lesson 1.3)
(A) 15,265
(B) 93,216
(C) 320,182
(D) 320,128
Answer:
320182 is the greatest number.
Option C is the correct answer.

Question 3.
Which number when rounded to the nearest thousand is 23,000? (Lesson 1.4)
(A) 22,097
(B) 22,499
(C) 23,400
(D) 23,501
Answer:
22,499 number is rounded to the nearest thousand is 23000.
Option B is the correct answer.

Question 4.
Simplify 20 + 10 × 19 – 7 (Lesson 2.7)
(A) 140
(B) 203
(C) 360
(D) 563
Answer: D
20 + 10 × 19 – 7 = 563
first by adding 20 with 10 we get 30
Now by multiplying 30 with 19 we get 570
From 570 if we remove 7 we get 563
Option D is the correct answer.

Question 5.
Multiply 52 × 10². (Lesson 2.3)
(A) 52
(B) 520
(C) 5,200
(D) 52,000
Answer: C
52 × 10² = 5200
the square of 10 is 100 now by multiplying 100 with 52 we get 5200
Option C is the correct answer.

Question 6.
Which is the difference between the value of the digit 6 in 2,300,628 and in 846,150? (Lesson 1.2)
(A) 600
(B) 5,400
(C) 5,522
(D) 6,000
Answer: B
Digit 6 in 2,300,628 is 600
And digit 6 in 846,150 is 6000
Option B is the correct answer.
Now buy removing 600 from 6000 we get 5400

Question 7.
Which is the remainder when 4,885 is divided by 21? (Lesson 2.6)
(A) 12
(B) 13
(C) 14
(D) 15
Answer:
Remainder is 13.
Option B is the correct answer.

Question 8.
Express 4 ÷ \(\frac{1}{12}\) in simplest form. (Lesson 4.6)
(A) 48
(B) 3
(C) \(\frac{4}{12}\)
(D) \(\frac{1}{48}\)
Answer:
\(\frac{1}{12}\) = 1/12
1/12 ÷ 4 = 3.
Option B is the correct answer.

Question 9.
Find the difference: \(\frac{3}{4}\) – \(\frac{3}{8}\). (Lesson 32)
(A) \(\frac{5}{8}\)
(B) \(\frac{3}{8}\)
(C) \(\frac{1}{2}\)
(D) \(\frac{1}{4}\)
Answer:
\(\frac{3}{4}\) = 3/4
\(\frac{3}{8}\) = 3/8
The difference is 3/4 – 3/8 = 3/8.

Question 10.
Find the product: \(\frac{3}{4}\) × \(\frac{8}{12}\)(Lesson 4.1)
(A) \(\frac{1}{2}\)
(B) \(\frac{2}{3}\)
(C) \(\frac{5}{12}\)
(D) \(\frac{11}{16}\)
Answer:
\(\frac{3}{4}\) = 3/4 \(\frac{8}{12}\) = 8/12
3/4 × 8/12 = 1/2 = \(\frac{1}{2}\)
Option A is the correct answer.

Question 11.
Estimate the sum of \(\frac{6}{7}\) and \(\frac{3}{5}\). (Lesson 3. 1)
(A) 0
(B) \(\frac{1}{2}\)
(C) 1\(\frac{1}{2}\)
(D) 1
Answer:
\(\frac{6}{7}\) = 6/7 \(\frac{3}{5}\) = 3/5
Sum = 6/7 + 3/5 = 1×1/2.
1\(\frac{1}{2}\)
Option C is the correct answer.

Question 12.
What is the difference between 3\(\frac{1}{2}\) and 1\(\frac{1}{4}\) (Lesson 3.6)
(A) 2\(\frac{1}{4}\)
(B) 3\(\frac{1}{4}\)
(C) 4\(\frac{3}{4}\)
(D) 4\(\frac{1}{2}\)
Answer:
3\(\frac{1}{2}\) = 3×1/2 1\(\frac{1}{4}\) = 1×1/4
Difference = 2×1/4 = 2\(\frac{1}{4}\)
Option A is the correct answer.

Question 13.

Find the area of triangle ABC. (Lesson 6.3)

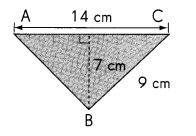
(A) 126 cm²
(B) 98 cm²
(C) 63 cm²
(D) 49 cm
Answer:D
Explanation:
Since area of triangle is A= (Hight × base) /2
Hight = 7 cm
base = 14 cm
so we have (7 × 14)/ 2
7 × 14 =98
98/2=49 cm
Option D is the correct answer.

Question 14.
Simplify 4x + 6 – 2x – 1
(A) 6x + 1
(B) 4x + 3
(C) 8x + 6
(D) 2x + 5
Answer:
Given:
4x + 6 – 2x -1
2x + 5
Option D is the correct answer.

Question 15.
For what value of y will the inequality 3y + 4 < 8 be true? (Lesson 5.4)
(A) y = 1
(B) y = 2
(C) y = 3
(D) y = 4
Answer:
3y + 4 < 8
Take y = 1
3(1) + 4 <8
7<8
Option A is the correct answer.

Question 16.
Glass A contains 236 milliliters of milk. Glass B contains 420 milliliters of milk. What is the ratio of the amount of milk in Glass A to that in Glass B? (Lesson 73)
(A) 89 : 135
(B) 119 : 165
(C) 479 : 660
(D) 59 : 105
Answer:
Glass A contains 236 milliliters of milk
Glass B contains 420 milliliters of milk
236 : 420
= 236/480 = 59/105
= 59 : 105
Option D is the correct answer.

Short Answer

Read the questions carefully. Write your answers in the space provided. Show your work.

Question 17.
What is the missing number in the box? (Lesson 1.2)
87,412 = 80,000 + + 400 + 10 + 2 ____
Answer:
87412 = 80000 + 7000 + 400 + 10 + 2

Question 18.
Order the numbers from greatest to least. (Lesson 1.3)

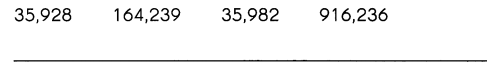
Answer:
916,236 > 164,239 > 35,982 > 35,928

Question 19.
Find the product of 238 and 4,000. (Lesson 2.2) _____
Answer:
The product of 238 and 4000 = 952000

Question 20.
Simplify 4 × {(43 – 19) + [(121 – 3) ÷ 2]}. (Lesson 2.7)
_____
Answer:
4 × {(43 – 19) + [(121 – 3) ÷ 2]} = 160.

Question 21.
There are 215 Grade 5 students in Cherrywood school. Each student spends $17 on a dictionary. How much in all do the students spend on the dictionary? (Lesson 2.8)
______
Answer:
Total number of students in a grade 5 = 215.
Each student’s spends on a dictionary = 215 × 17 = $ 3655

Question 22.
Mr. Hull is buying computer equipment for his company. The equipment costs $45,900. He pays $5,300 for the first payment. He then pays the rest of the amount in equal payments for 1 4 months. Find the amount he has to pay each month. (Lesson 28)
_________
Answer:
Mr. Hull is buying computer equipment for his company.
The equipment cost = $45900
He pay for the first payment = 5300
He then pay the rest of the amount in equal payments for 14 months.
45900 – 5300 = 40600
40600 ÷ 4 = 2900.

Question 23.
Simplify (2 + 4) × 7 – 6 + 11. (Lesson 2.7)
______
Answer:
(2 + 4) × 7 – 6 + 11
6 × 1 + 11
6 × 12 = 72

Question 24.
Express 38 ÷ 6 as a fraction in simplest from. Then rewrite the fraction as a mixed number. (Lesson 3.3)
_____
Answer:
38 ÷ 6 is in the simplest form = 6.3333

Question 25.
Shaun has 24\(\frac{1}{2}\) ounces of beads. He has 3\(\frac{3}{8}\) ounces of beads less than Tony. Find the weight of Tony’s beads. (Lesson 3.7)
_________
Answer:
Shaun has 24\(\frac{1}{2}\) ounces of beads.
Shaun has 3\(\frac{3}{8}\) ounces of beads less than Tony.
The weight of Tony’s beads = 24\(\frac{1}{2}\) + 3\(\frac{3}{8}\) = 27×\(\frac{7}{8}\)

Question 26.
Express 24\(\frac{1}{4}\) – 15\(\frac{1}{2}\) as a decimal. (Lessons 3.3 and 3.6)
_________
Answer:
24×\(\frac{1}{4}\) – 15×\(\frac{1}{2}\) = 8.75

Question 27.
Lita jogged 7\(\frac{3}{10}\) kilometers on Friday. She jogged 1\(\frac{3}{4}\) kilometers more on Saturday. How many kilometers did she jog on both days? Give your answer as a decimal. (Lesson 3.7)
___________
Answer:
Lita jogged 7×10+3 kilometres on Friday
She jogged 1×4+3 kilometres on Saturday.
She jog on both days = 73 + 7 = 80 kilometres.
80 in decimal = 0.8

Question 28.
Multiply \(\frac{70}{6}\) by \(\frac{18}{4}\). Express the product as a mixed number in simplest form. (Lesson 4.3)
Answer:
\(\frac{70}{6}\) = 70/6 \(\frac{18}{4}\) = 18/4
Product of numbers = 52×1/2

Question 29.
Jamal runs 1\(\frac{3}{10}\) miles a day to train for a race. (Lesson 4.5)

a. If he runs the same distance for 3 days a week, what is the distance he runs in one week?
Answer:
Jamal runs 1×10+3 miles a day to train for a race = 33 miles per a day.
If he runs the same distance for 3 days in a week.
Distance he runs in 1 week = 33 × 3 = 99 miles

b. If he keeps to this training regime for 8 weeks, what is the total distance he will run in 8 weeks?
Answer:
If he keeps to this training regime for 8 weeks.
Total distance he will run in 8 weeks =
1 week = 7 days.
8 weeks = 7×8 = 56
Therefore 33 × 56 = 1848 miles.

Question 30.
A ball of string \(\frac{9}{10}\) meter long is cut into 3 pieces of the same length. Find the length of each piece. (Lesson 4.6)
Answer:
\(\frac{9}{10}\) = 9/10
Ball of string meter long is cut into 3 pieces of the same length = 9/10 ÷ 3 = 3/10.

Question 31.
3 batteries cost $5rand 8 folders cost $2r. Jason bought 6 batteries and 4 folders. How much does he pay? Give your answer in terms of r. (Lesson 5.5)
Answer:
3 batteries cost = $5r
8 folders cost = $2r
Jason bought 6 batteries and 4 folders
6 batteries cost = 3 batteries + 3 batteries = $5r + $5r = $10r.
4 folders cost = $1r
Jason pay = $10r + $1r = $11r.

Question 32.
Find the area. (Lesson 6.1)

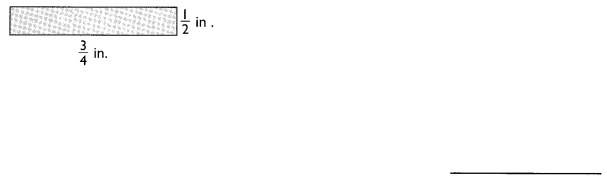
Answer:

Question 33.
The base of the triangle ABC is as given. Label its height. (Lesson 6.2)

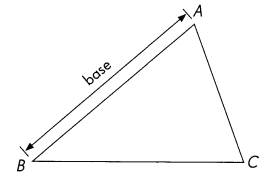
Answer:

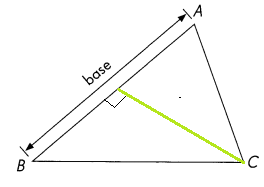
Question 34.
Find the area of triangle PQR. (Lesson 6.3)

Answer: 56cm
Explanation:
Since we know area of triangle 1/2  × BH
B= base = 7 cm
H= Hight = 16cm
so,
1/2 × (7 × 16)
1/2 × (112)
56cm

Question 35.
ABCD and ECFG are rectangles. BC = CF. What is the total area of the shaded parts of the figure? (Lesson 6.3)

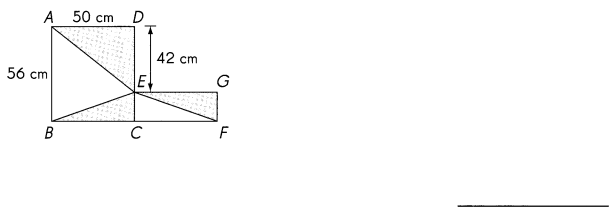
Answer: 1750 cm
Explanation:
area of triangle is (BH)/2
for triangle ADE area is
\(\frac{1}{2}\) × (42 × 50) = 1050
for triangle EGF area is
\(\frac{1}{2}\) × (14 × 50) = 350
for triangle BCE area is
\(\frac{1}{2}\) × (14 × 50) = 350
Now by adding all the three we get the total area of the shaded region
that is
1050+350+350=1750 cm

Question 36.
The ratio of the masses of flour in two bags is 5 : 7. The heavier bag contains 1,120 grams of flour. What is the total mass of flour in both bags? (Lesson 7.3)
_________
Answer:
Explanation:
Given:
5 : 7
? : 1,120
Consider x as the other bag content
5 : 7
x : 1,120
by cross multiplication we get
5 × 1120 = 7 × x
5600 = 7x
x=5600/7
x=\(\frac{5600}{7}\)
x=800
therefore the lighter bag contains 800 grams of flour.
Now by adding both we get the total mass of flour in both bags
that is
800 + 1120 = 1920 grams

Question 37.
Rachel, Sally, and Fabio share a pie in the ratio 1 : 2 : 4. What fraction of the pie does Sally get? (Lesson 7.6)
Answer:
Explanation:
Given:
Total shares of pie  present = 1 + 2 + 4 = 7
Rachel’s share = \(\frac{1}{7}\)
Sally = \(\frac{2}{7}\)
Fabio = \(\frac{4}{7}\)
so, fraction of the pie does Sally get is \(\frac{2}{7}\) which is 2/7

Question 38.
The lengths of three sides of a triangle are in the ratio 3 : 4 : 5. The perimeter of the triangle is 156 centimeters. What is the difference in length between the longest and shortest sides? (Lesson 7.6)
___________
Answer:
Explanation:
Given:
lengths of three sides of a triangle are in the ratio 3 : 4 : 5
the perimeter of the triangle is 156 centimeters
Total lengths of three sides of a triangle = 3 + 4 + 5 = 12
Now divide 12 with 156
The quotient will be 13
which means each unit is equal to 13
that is 1 unit =  13
so
for 3 it is = 13 + 13 + 13 = 39
for 4 it is = 13 + 13 + 13 + 13 = 52
for 5 it is = 13 + 13 + 13 + 13 = 65
Now the shortest sides = 39
And the longest side = 65
The difference in length between the longest and shortest sides = 65 – 39 = 26 cm

Question 39.
Look for a pattern in this set of figures. (Lesson 5.1)

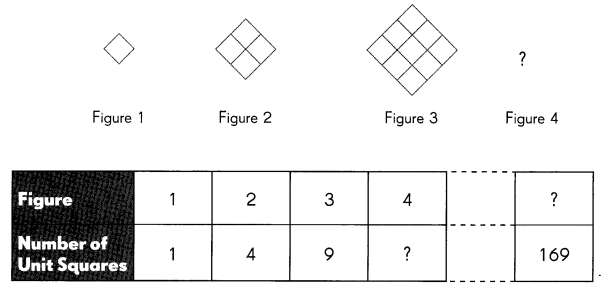
a. How many unit squares are in Figure 4? ____
Answer:
16 unit squares are in the figure 4.

b. Which figure in this pattern will have 169 small squares? ____
Answer:
Figure 13 is in the pattern will have 169 small squares.

Extended Response

Solve. Show your work.

Question 40.
Poles are placed an equal distance apart along a 6-kilometer road. There is a tree in between every two poles. The figure shows the distance between a tree and two poles. Poles are placed at the start and end of the road. How many poles are there? (Lesson 2.5)

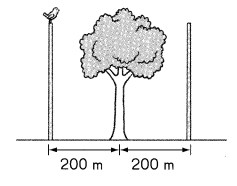
Answer:
Given that
Poles are placed an equal distance a part along a 6 kilometres on road.
Every tree between two poles.
6 kilometres = 6000 meters
Distance between 2 poles = 400m.
6000/400 = 15.
There are 15 trees together and there are 16 poles together.

Question 41.
A whole number when divided by 4 gives a remainder of 3. The same whole number when divided by 6 gives a remainder of 1. The number is between 70 and 85. What is the number? (Lesson 2.6)
Answer:
The whole number is 79.
79 ÷ 4  the remainder = 3
79 ÷ 6 the remainder = 1

Question 42.
Sarah earns $525 more than Andrew each month. They each spend $1,250 a month and save the rest. Sarah does not have any savings at first. After 11 months, she has $8,250 in savings. How much does Andrew earn in a year? (Lesson 2.8)
Answer:
Explanation:
Given:
Sarah earns $525 more than Andrew each month
They each spend $1,250 a month
After 11 months, she has $8,250 in savings
so, we get
8250 ÷ 11 = 750
Total amount Sarah earns per month is
1250 + 750 = 2000
Total amount Andrew earns per month is
2000 – 525 =1475
So,Andrew earn in a year is
1475 × 12 = 17700 per year

Question 43.
Ivan caught a total of 7\(\frac{2}{5}\) pounds of fish one day. Of the fish caught, 4\(\frac{5}{8}\) pounds were sea bass and the rest were mackerel. He gave away 1\(\frac{7}{8}\) pounds of mackerel. How many pounds of mackerel did he have left? Give your answer as a decimal. (Lesson 3.7)
Answer: \(\frac{36}{40}\) = \(\frac{9}{10}\) = 0.9lbs of mackerel

Question 44.
There were 2\(\frac{4}{5}\) quarts of milk in Container A and some milk in Container B. Lisa poured 1\(\frac{2}{5}\) quarts of milk each into Container A and Container B. In the end, the total volume of milk in the two containers was 10 quarts. How many quarts of milk were in Container B at first? Give your answer as a decimal. (Lesson 3.7)
Answer: 4\(\frac{2}{5}\) = 4\(\frac{4}{10}\) = 4.4 qts

Question 45.
Tyrone read a book for his school project. On the first day, he read 40 pages. On the second day, he read \(\frac{1}{4}\) of the remaining pages. After the second day, he still had to read \(\frac{1}{2}\) of the total number of pages to complete the book. How many pages are in the book? (Lesson 4.2)
Answer:
day one = 40 pages
Total of 6 units
one unit = 20
so for six unit
6 × 20
= 120 pages of book

Question 46.
A dealership has 9y cars, 12y trucks and 18 vans. (Lesson 5.5)

a. 4y cars, 3y trucks and 15 vans are sold. Find the total number of vehicles remaining in terms of y.
Answer:
A dealership has 9y cars, 12y trucks and 18 vans.
He sold 4y cars, 3y cars 15 vans.
Remaining vehicles = 9y – 4y = 5y
12y – 3y = 9y
18 – 15 = 3
Remaining vehicles are 5y cars, 9y trucks and 3 vans.

b. If the value of y is 7, are there more trucks or more cars and vans at first?
Answer:
5y + 9y = 14y
14(7) = 68
There are more trucks at first.

Question 47.
The side of square JKLM is 14 inches. KP = MP = JP = LP. Find the total area of the shaded parts. (Lesson 6.3)

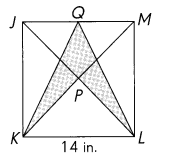
Answer:
Given:
We know the area for triangle is = (BH)/2
For triangle KLQ are is
area =\(\frac{1}{2}\) ×  (14 × 14)
area =\(\frac{1}{2}\) ×  (196)
area =98 in
For triangle KLP are is
area =\(\frac{1}{2}\) ×  (14 × 7)
area =\(\frac{1}{2}\) ×  (98)
area =49 in
The total area of the shaded parts is
98 – 49 = 49 in

Question 48.
Freddie has 2 times as many comic books as David. The ratio of the number of comic books David has to the number of comic books Gary has is 5 : 3. Freddie has 110 comic books. How many comic books do David and Gary have in total? (Lesson 7.6)
Answer: 88 comic books
Explanation:
Given:
Freddie has 2 times as many comic books as David
The ratio of the number of comic books David has to the number of comic books Gary has is
5 : 3
Freddie has 110 comic books which is 2 times David that is 10
so Freddie has 10 units
David has 5 units
And, Gary has 3 units
10 + 5 + 3 = 18 unit
As Freddie has 110 comic books with 10 units
then each unit is = 11
comic books David and Gary have in total is
5 + 3 = 8 × 11 = 88 comic books

Question 49.
The ratio of the volume of water in Container A to the volume of water in Container B to the volume of water in Container C is 2 : 3 : 8. Container B contains 900 milliliters of water. (Lesson 7.6)

a. What is the volume of water in Container C?
Answer: 2400 milliliters of water
Explanation:
Given:
The ratio of the volume of water in Container A to the volume of water in Container B to the volume of water in Container C is 2 : 3 : 8
A : B : C
2 : 3 : 8
consider B and C container
so we will have
3 : 8
900 : ?
put x in place of the unknown value
we get
3 : 8
900 : x
By cross multiplication we get
3x = 8 × 900
3x = 7200
x = 7200/3
x = \(\frac{7200}{3}\)
x = 2400 milliliters of water
The volume of water in Container C 2400 milliliters of water

b. Find the total volume of water in the three containers.
Answer: 3900 milliliters of water
Explanation:
Given:
The ratio of the volume of water in Container A to the volume of water in Container B to the volume of water in Container C is 2 : 3 : 8
A : B : C
2 : 3 : 8
x : 900 : 2400
consider A and B
2 : 3
x : 900
By cross multiplication we get
3x = 2 × 900
3x = 1800
x= 1800/3
x =  \(\frac{1800}{3}\)
x = 600
now for total volume of water in the three containers add all the three values that is
600 + 900 + 2400 =3900 milliliters of water

Question 50.
Belinda has 10 cups of flour. She uses 3 cups of it to make a loaf of bread. She uses \(\frac{1}{4}\) cup of the remaining flour for each biscuit she wants to make. How many biscuits can she make with the remaining flour?
Answer: 24 biscuit
Given:
Belinda has 10 cups of flour
She uses 3 cups of it to make a loaf of bread.
so , we get
10 – 3 = 7
Now the remaining flour for each biscuit she wants to make.= \(\frac{1}{4}\)
7 × 4
24 biscuit

Questions 51.
Mr. Madison has two boxes of blueberries. At first, Box A had 228 more blueberries than Box B. Mr. Madison transfers 600 blueberries from Box A to Box B. Now Box B contains 5 times as many blueberries as Box A.
How many blueberries were in each box at the beginning?

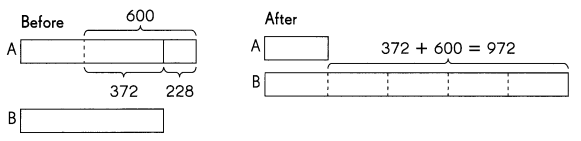
Answer:
Explatation:
Given:
Box A = 228 more than B
Box B = 5Box A
In box A
243 + 600 = 843
In box B
843 – 288 =615