Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 1 Review Test to finish your assignments.
Math in Focus Grade 7 Course 2 A Chapter 1 Review Test Answer Key
Concepts and Skills
Write each number in \(\frac{m}{n}\) form where m and n are integers with n ≠ 0. Simplify your answers.
Question 1.
20.75
Answer:
20.75 = 83/4
Explanation:
The given decimal number 20.75 is represented in m/n form. The m/n form of 20.75 is 83/4.
Question 2.
-0.48
Answer:
-0.48 = -12/25
Explanation:
The given decimal number -0.48 is represented in m/n form. The m/n form of -0.48 is -12/25.
Question 3.
4\(\frac{6}{13}\)
Answer:
4(6/13)
= (52 + 6)/13
= 58/13
Explanation:
The given mixed fraction is 4(6/13). The simplified mixed fraction is represented in m/n form. The m/n form of 4(6/13) is 58/13.
Question 4.
–\(\frac{39}{56}\)
Answer:
-39/56
Explanation:
The given number -39/56 is already in m/n form.
Question 5.
1.34
Answer:
1.34 = 134/100 = 67/50
Explanation:
The given decimal number 1.34 is represented in m/n form. The m/n form of 1.34 is 134/100 or 67/50.
Question 6.
60%
Answer:
60% = 60/100
Explanation:
The given number 60% is represented in m/n form. The m/n form of 60% is 60/100.
For each pair of numbers, find the absolute value of each number. Then, determine which number is farther from 0 on the number line.
Question 7.
—16 and —18
Answer:
The absolute value of the number|-16| is 16.
The absolute value of the number |-18| is 18.
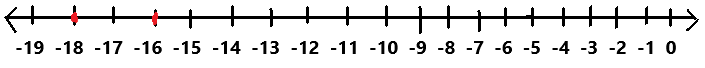
Explanation:
In the above image we can observe a number line.
The absolute value of |-16| is 16. So the number -16 is 16 units from 0.
The absolute value of |-18| is 18. So the number -18 is 18 units from 0.
So, the number -18 is farther from 0 on the number line.
Question 8.
–\(\frac{15}{4}\) and \(\frac{18}{7}\)
Answer:
-15/4 and 18/7
The absolute value of |-15/4| is 15/4.
The absolute value of |18/7| is 18/7.
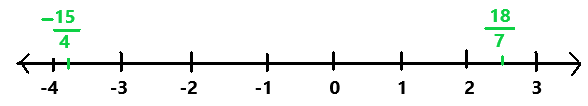
Explanation:
In the above image we can observe a number line.
The absolute value of |-15/4| is 15/4. So the number -15/4 is 15/4 units from 0.
The absolute value of |18/7| is 18/7. So the number 18/7 is 18/7 units from 0.
So, the number -15/4 is farther from 0 on the number line.
Question 9.
2.36 and -2.7
Answer:
2.36 and -2.7
The absolute value of |2.36| is 2.36.
The absolute value of |-2.7| is 2.7.
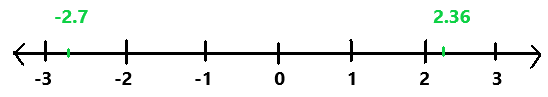
Explanation:
In the above image we can observe a number line.
The absolute value of |2.36| is 2.36. So the number 2.36 is 2.36 units from 0.
The absolute value of |-2.7| is 2.7. So the number -2.7 is 2.7 units from 0.
So, the number -2.7 is farther from 0 on the number line.
Question 10.
\(\frac{31}{3}\) and \(\frac{40}{6}\)
Answer:
31/3 and 40/6
The absolute value of |31/3| is 31/3.
The absolute value of |40/6| is 40/6.

Explanation:
In the above image we can observe a number line.
The absolute value of |31/3| is 31/3. So the number 31/3 is 31/3 units from 0.
The absolute value of |40/6| is 40/6. So the number 40/6 is 40/6 units from 0.
So, the number 31/3 is farther from 0 on the number line.
Using long division, write each rational number as a decimal. Use the bar notation if the rational number is a repeating decimal.
Question 11.
\(\frac{7}{56}\)
Answer:
7/56
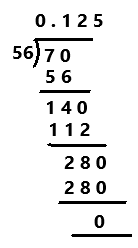
Explanation:
A Decimal Number that contains a finite number of digits next to the decimal point is called a Terminating Decimal. Perform division operation on given rational number. By using long division method, divide 56 by 7 the quotient is 0.125 which is a terminating decimal.
Question 12.
9\(\frac{13}{20}\)
Answer:
9(13/20)
= (180 + 13)/20
= 193/20
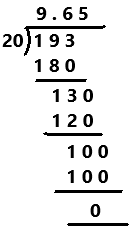
Explanation:
Perform division operation on given rational number. The mixed fraction 9(13/20) in fraction form is 193/20. By using long division method, divide 193 by 20 the quotient is 9.65 which is a terminating decimal.
Question 13.
\(\frac{100}{11}\)
Answer:
100/11
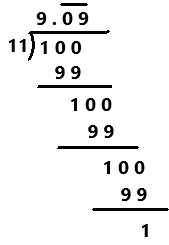
Explanation:
A repeating decimal is decimal representation of a number whose digits are periodic and the infinitely repeated portion is not zero.
Perform division operation on given rational number. By using long division method, divide 100 by 11 the quotient is 9.0909… which is a repeating decimal. The repeating decimals are denoted by the bar notation as we can observe in the above image.
Question 14.
–\(\frac{5}{12}\)
Answer:
-5/12
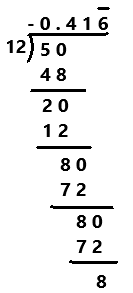
Explanation:
Perform division operation on given rational number. By using long division method, divide -5 by 12 the quotient is -0.41666… which is a repeating decimal. The repeating decimals are denoted by the bar notation as we can observe in the above image.
Question 15.
-2\(\frac{9}{55}\)
Answer:
-2(9/55)
= -(110 + 9)/55
= -119/55
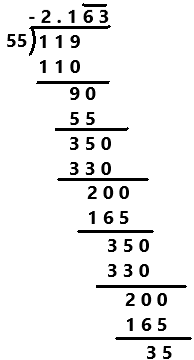
Explanation:
Perform division operation on given rational number. The mixed fraction of -2(9/55) in fraction form as -119/55. By using long division method, divide -119 by 55 the quotient is -2. 16363… which is a repeating decimal. The repeating decimals are denoted by the bar notation as we can observe in the above image.
Question 16.
47%
Answer:
47%
= 47/100
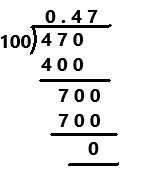
Explanation:
Perform division operation on given rational number. The 47% in fraction form is 47/100. By using long division method, divide 47 by 100 the quotient is 0.47 which is a terminating decimal.
Problem Solving
Use the irrational numbers below for questions 17 to 20.
![]()
Question 17.
Using rational numbers, find a segment with a distance of not more than 0.1 to locate each irrational number approximately on the real number line.
Answer:
The irrational number \(\sqrt{31}\) lies between the rational numbers with a distance of not more than 0.1 are 5.5 and 5.6.
5.5 < \(\sqrt{31}\) < 5.6
The irrational number –\(\sqrt{112}\) lies between the rational numbers with a distance of not more than 0.1 are -10.6 and -10.5.
-10.6 < –\(\sqrt{112}\) < -10.5
The irrational number ∛142 lies between the rational numbers with a distance of not more than 0.1 are 5.2 and 5.3.
5.2 < ∛142 < 5.3
The irrational number -(1/4) π³ lies between the rational numbers with a distance of not more than 0.1 are -7.8 and -7.7.
-7.8 < -(1/4) π³ < -7.7
Question 18.
Write a rational approximation of each irrational number correct to 2 decimal places.
Answer:
\(\sqrt{31}\) = 5.5776
The rational approximation of irrational number \(\sqrt{31}\) is 5.58.
–\(\sqrt{112}\) = – 10.58300
The rational approximation of irrational number –\(\sqrt{112}\) is -10.58.
∛142 = 5.21710
The rational approximation of irrational number ∛142 is 5.22.
-(1/4) π³ = – 7.75156
The rational approximation of irrational number -(1/4) π³ is -7.75.
Question 19.
Graph on a real number line the interval and the approximate location of each irrational number.
Answer:
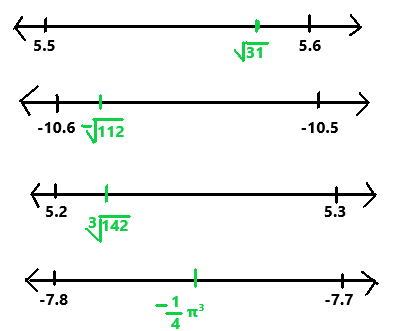
The given irrational numbers on the number lines as we can observe in the above image.
Question 20.
Order the irrational numbers from greatest to least using the symbol >.
Answer:
The given irrational numbers from greatest to least are \(\sqrt{31}\) > ∛142 > -(1/4) π³ > –\(\sqrt{112}\)
Use the real numbers below for questions 21 to 24.
-12\(\frac{3}{8}\), \(\frac{90}{7}\), –\(\sqrt{49}\), \(\sqrt{164}\), -8.207
Question 21.
Find the absolute value of each real number in decimal form, correct to three decimal places.
Answer:
-12(3/8)
= -(96 + 3)/8
= – 99/8
The absolute value of |-99/8| is 99/8.
The decimal form of 99/8 is 12.375.
90/7
The absolute value of |90/7| is 90/7.
The decimal form of 90/7 is 12.8571.
The decimal value 12.8571 is corrected to three decimal places is 12.857.
–\(\sqrt{49}\)
The absolute value of |-\(\sqrt{49}\)| is \(\sqrt{49}\).
The decimal form of \(\sqrt{49}\) is 7.000.
\(\sqrt{164}\)
The absolute value of |\(\sqrt{164}\)| is \(\sqrt{164}\).
The decimal form of \(\sqrt{164}\) is 12.8062.
The decimal value 12.8062 is corrected to three decimal places is 12.806.
-8.207
The absolute value of |-8.207| is 8.207.
Question 22.
Graph each real number on a real number line.
Answer:
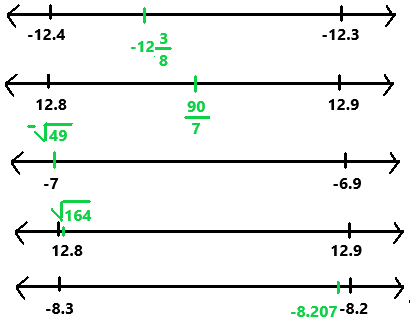
questions 23.
Order the numbers from least to greatest using the symbol <.
Answer:
The given real numbers from least to greatest are -12\(\frac{3}{8}\) < -8.207 < –\(\sqrt{49}\) < \(\sqrt{164}\) < \(\frac{90}{7}\).
Question 24.
Math Journal Explain why the product of a nonzero rational number and an irrational number is irrational.
Answer:
The product of a non- zero rational and an irrational number is irrational because if we add any rational value to an irrational number it remains irrational.
Solve.
Question 25.
Round each number to the given number of significant digits.
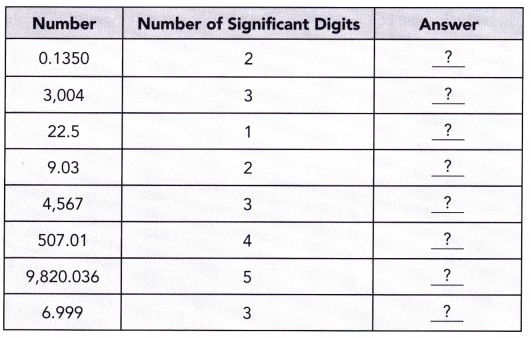
Answer:
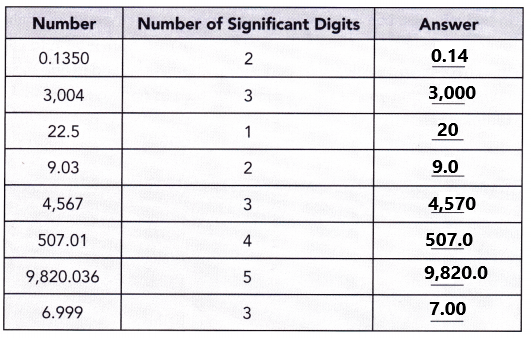
Question 26.
The distance between New York City, New York, and Sydney, Australia, is about 15,989 kilometers. What is this distance when rounded to 2 significant digits?
Answer:
The distance between New York City, New York, and Sydney, Australia, is 15,989 kilometers. After rounding to 2 significant digits the distance is 16,000 kilometers.
Question 27.
A dime has a mass of 2.268 grams. Round the mass of the dime to 3 significant digits.
Answer:
The dime has a mass of 2.268 grams. After rounding the mass of the dime to 3 significant digits the mass is 2.27 grams.
Question 28.
In 2009, the population of New York City was estimated at 8,391,881. Round this population estimation to the given number of significant digits.
a) 2 significant digits
Answer:
The given population 8,391,881 is rounded to 2 significant digits as 8.3 million.
b) 3 significant digits
Answer:
The given population 8,391,881 is rounded to 3 significant digits as 8.39 million.
c) 4 significant digits
Answer:
The given population 8,391,881 is rounded to 4 significant digits as 8,392 thousands.
Question 29.
A square has an area of 72 square inches. What is the length of a side of the square correct to 2 significant digits?
Answer:
A square has an area of 72 square inches.
Length of square = ?
Area of the square = side x side
72 = s²
\(\sqrt{72}\) = s
8.485 = s
8.5 inches = length of a side
The length of a side of the square is corrected to 2 significant digits as 8.5 inches.