Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 7 Lesson 7.4 Constructing Quadrilaterals to score better marks in the exam.
Math in Focus Grade 7 Course 2 B Chapter 7 Lesson 7.4 Answer Key Constructing Quadrilaterals
Math in Focus Grade 7 Chapter 7 Lesson 7.4 Guided Practice Answer Key
Construct the quadrilateral from the given dimension. Use a ruler and protractor.
Question 1.
Rectangle ABCD measuring 7 centimeters by 5 centimeters.
Explanation:
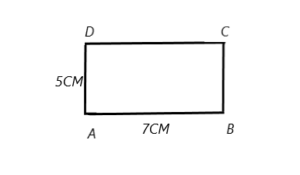
Answer:
we have drawn the rectangle with the measurements of length=5cm and breadth=7cm.
Construct the quadrilateral from the given information. Use a compass, ruler, and protractor.
Question 2.
Parallelogram KLMN: KL = 6.4 cm, LM = 4.8 cm, and m∠KLM = 60°.
Explanation:
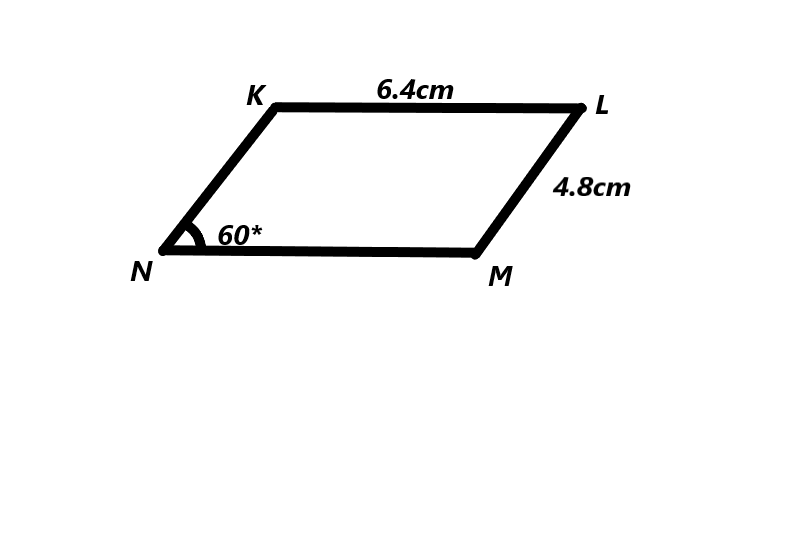
Answer:
The measurements of the parallelogram of length= 4.8cm and breadth=6.4cm. The angle of KLM=60.
Construct the quadrilateral from the given
information. Use a ruler, compass, and protractor.
Question 3.
Rhombus PQRS with diagonal PR = 6.2 cm and PQ = 4.5 cm.
Explanation:
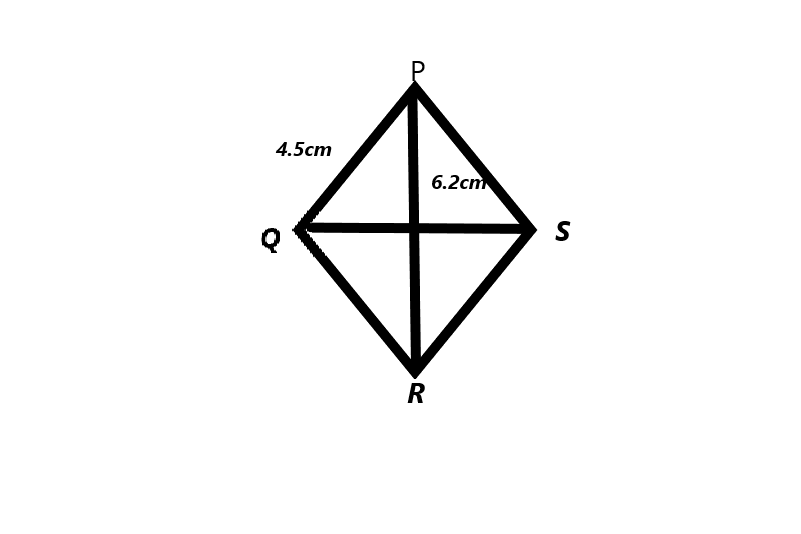
Answer:
we drawn the rhombus with the measurement angels of PR=6.2cm and PQ=4.5cm.
Math in Focus Course 2B Practice 7.4 Answer Key
Construct each quadrilateral from the given information.
Question 1.
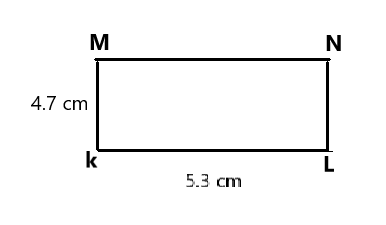
Rectangle KLMN measuring 5.3 centimeters by 4.7 centimeters.
Answer:
The measuring angles of rectangle is Length = 5.3 cm and breadth= 4.7 cm
Explanation:
Question 2.
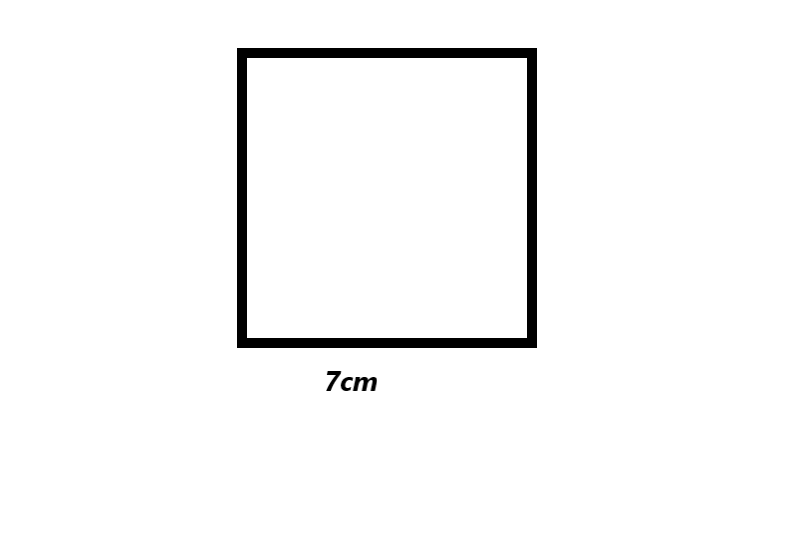
Square with side lengths of 7 centimeters.
Explanation:
Answer:
The measuring angles of the square is 7cm.
Question 3.
Rhombus DEFG with diagonal DF = 6 cm and DE = 4.5 cm.
Explanation:
Answer:
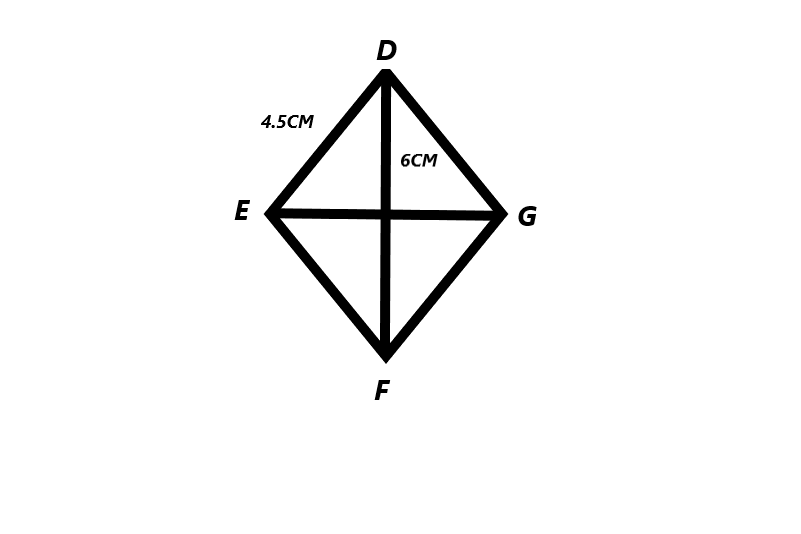
The measuring angles of the rhombus DEFG diagonals DF=6cm and DE=4.5cm.
Question 4.
Parallelogram PQRS with PQ = 3.8 cm, QR = 5 cm, and m∠QPS = 70°.
Answer:
Explanation:
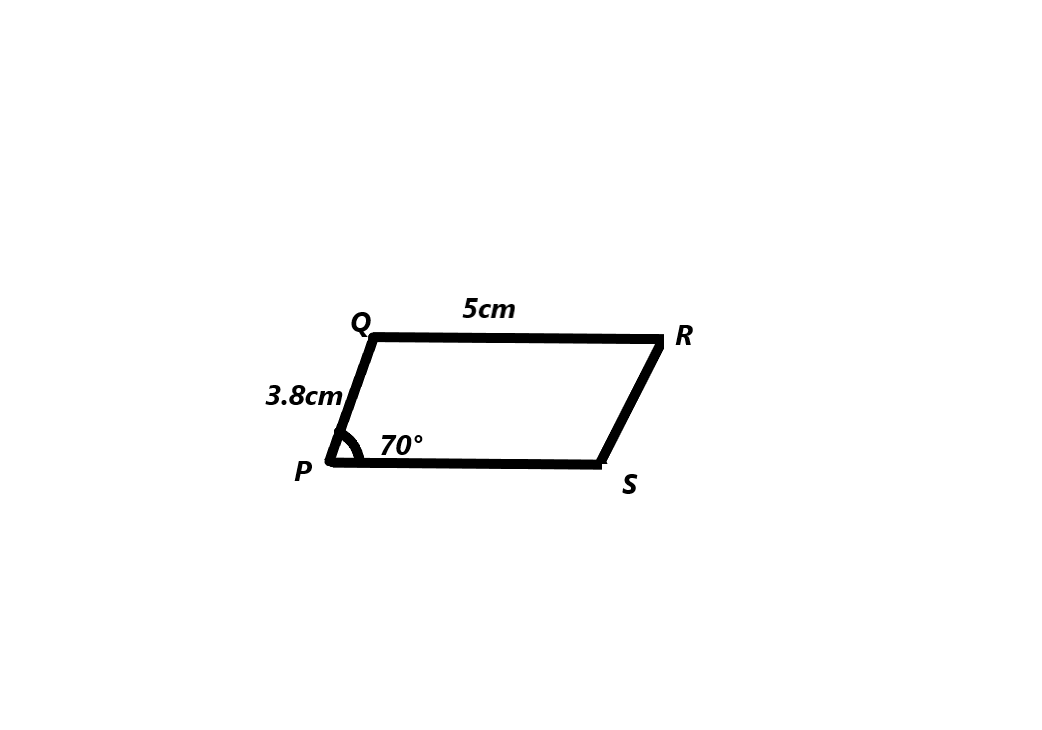
The measuring angles of the parallelogram PQRS
PQ=3.8cm and QR=5cm
we got the angle 70°.
Question 5.
Quadrilateral ABCD with AB = 6.7 cm, BC = 7.2 cm, AD = 4.9 cm, CD = 6.2 cm, and m∠ABC = 55°.
Answer:
Explanation:
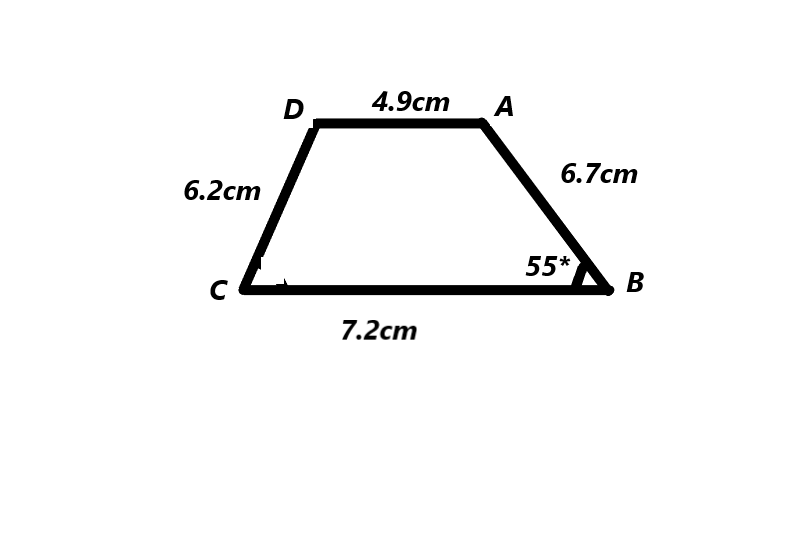
The measurements of quadrilateral ABCD of AB = 6.7, BC = 7.2, CD = 6.2 and DA = 4.9. We got the angle ABC = 55°.
Solve. Show your work.
Question 6.
Construct quadrilateral ABCD with diagonal AC = 5 cm, AB = CD = 4 cm, BC = 6 cm, and AD = 6 cm.
Answer:
Explanation:
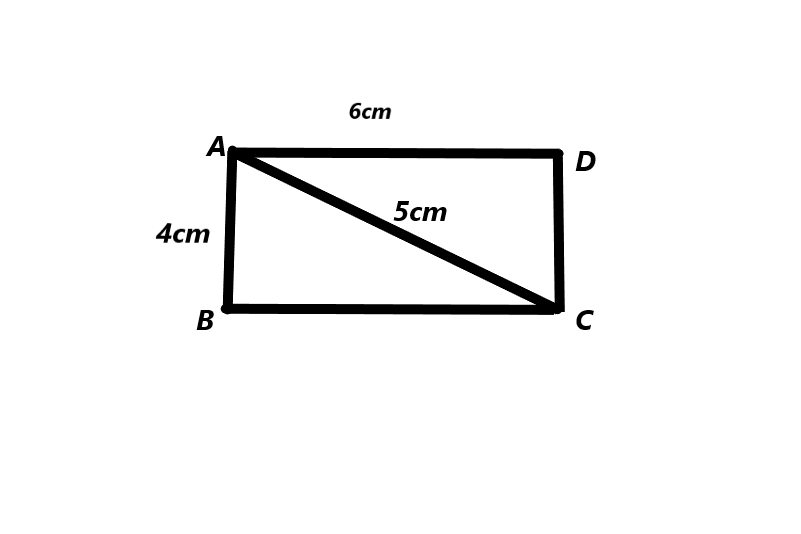
The measurements of the rectangular quadrilateral is AB = CD = 4cm , BC and AD = 6cm. The diagonal AC = 5cm. So this is a quadrilateral rectangular.
We sketch the quadrilateral:
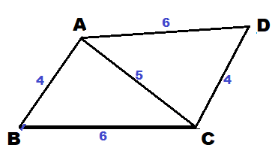
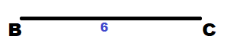
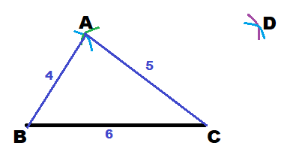
First we construct △ABC.
Use a ruler to draw the segment 6 cm long. Label its endpoints by B and C.
Because AB = 4 cm, use the ruler to set the compass to a radius of 4 cm. Then using B as center draw an arc of radius 4 cm above \(\overline{B C}\).
Because AC = 5 cm, use the ruler to set the compass to a radius of 5 cm. Then using C as center draw an arc of radius 5 cm that intersects the first arc. Label the intersection as A.
Use the ruler to draw \(\overline{A B}\) and \(\overline{A C}\).
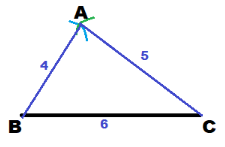
Then we construct △ACD.
Because AD = 6 cm, use the ruler to set the compass to a radius of 6 cm. Then using A as center draw an arc of radius 6cm above \(\overline{A C}\).
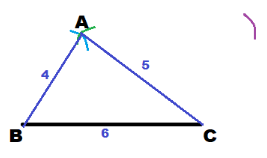
Because CD = 4 cm, use the ruler to set the compass to a radius of 4 cm. Then using C as center draw an arc of radius 4 cm that intersects the first arc. Label the intersection as D.
Use the ruler to draw \(\overline{A D}\) and \(\overline{C D}\).
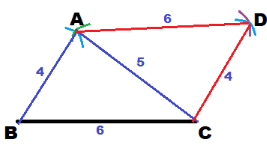
a) What type of quadrilateral is ABCD? Explain your reasoning.
Answer:
The quadrilateral ABCD is rectangle because the angles AB and CD are equal with the =4cm and the angles BC and AD are equal with the = 6cm. So this is rectangular quadrilateral.
b) Draw \(\overline{B D}\) to intersect \(\overline{A C}\) at point E. Find the lengths of \(\overline{A E}\), \(\overline{C E}\), \(\overline{B E}\), and \(\overline{D E}\).
Answer:
Draw \(\overline{B D}\)
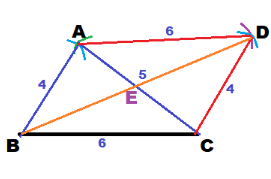
We measure AE, CE, BE, DE:
AE = 2.5
CE = 2.5
BE = 4.4
DE = 4.4
c) Do the diagonals \(\overline{A C}\) and \(\overline{B D}\) bisect each other? Justify your answer.
Answer:
The diagonals \(\overline{A C}\) and \(\overline{B D}\) bisect each other This is explained by the fact that the quadrilateral is a parallelogram.
Question 7.
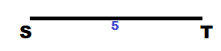
Construct a quadrilateral STUV by following Steps 1 to 5.
STEP1
Draw \(\overline{S T}\) so that ST = 5 cm.
STEP 2
With T as the center, draw \(\overline{T U}\) perpendicular to \(\overline{S T}\) , with TU = 4 cm.
STEP 3
With U as the center, draw an arc of radius 5 centimeters.
STEP 4
With S as the center, draw an arc of radius 4 centimeters to intersect the arc drawn in Step 3. Label this point of intersection as V.
STEP 5
Complete the construction of quadrilateral STUV.
Answer:
Use a ruler to draw \(\overline{S T}\) so that is 5 cm long.
Using a protractor, draw ∠T with a measure of 90°.
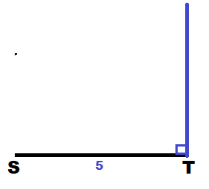
Because TU = 4 cm, set the compass to a radius of 4 cm. Then using T as the center, draw an arc intersecting the ray drawn in previous step. Label this point of intersection as U.
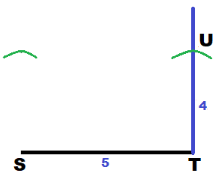
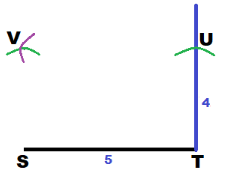
With U as center, draw an arc of radius 5 cm.
With S as center, draw an arc of radius 4 cm to intersect the arc drawn in the previous step. Label this point of intersection as V.
Draw \(\overline{V U}\) and \(\overline{V S}\).
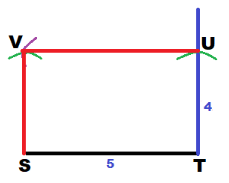
a) Find each of the angles in quadrilateral STUV.
Answer:
We measure the angles of the quadrilateral:
m∠T = 90°
m∠U = 90°
m∠V = 90°
m∠S = 90°
b) Name the quadrilateral.
Answer:
As all angles are right angles, the quadrilateral is a rectangle.
c) Find the lengths of the diagonals. What do you notice?
Answer:
We find the lengths of the diagonals:
SU ≈ 6.4
VT ≈ 6.4
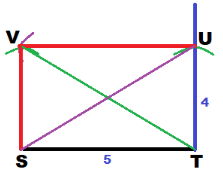
The diagonals are congruent.
Question 8.
Construct a quadrilateral ABCD with all sides of length 3 centimeters and diagonal BD = 5.2 cm.
a) What type of quadrilateral is ABCD? Explain your reasoning.
Answer:
Explanation:
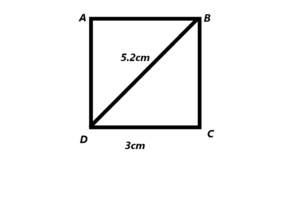
The quadrilateral ABCD is a square because the sides of the square AB, BC, CD and DA are equal with 3 cm and the diagonal BD=5.2cm.
b) Find the measure of each of the angles formed by the intersection of the diagonals.
Answer:
The measuring of each of the angles formed by the intersection of the diagonals is acute angle 60°.
Question 9.
Construct quadrilateral ABCD with diagonal AC = 6 cm, AB = 3 cm, BC = 4 cm, CD = 4.5 cm, and AD = 9 cm. What type of quadrilateral does ABCD seem to be? Explain your reasoning.
Answer:
Explanation:
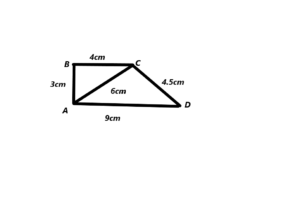
The quadrilateral ABCD is trapezoid. AB=3cm ,BC=4cm,CD=4.5cm and DA=9cm.
The diagonal AC = 6cm.So this is trapezoid.
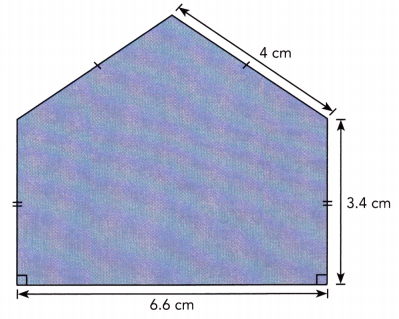
Question 10.
Construct the figure below using the given dimensions.
Answer:
Use a ruler to draw \(\overline{A B}\) so that is 6.6 cm long.
![]()
Using a protractor, draw ∠B with a measure of 90° and ∠A with a measure of 90°.
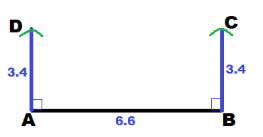
Because AD = BC = 3.4 cm, set the compass to a radius of 3.4 cm. Then using A and B as centers, draw arcs intersecting the rays drawn in previous step. Label this points of intersection as D and C.
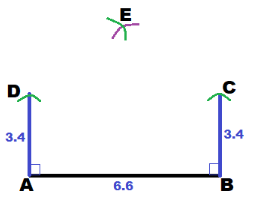
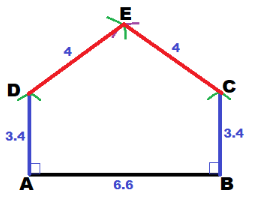
Because AE = EC = 4 cm, set the compass to a radius of 4 cm. Then using C and D as centers, draw arcs above \(\overline{C D}\). Label the point of intersection of the two arcs as E.
Draw \(\overline{E D}\) and \(\overline{E C}\).
Question 11.
a) Construct quadrilateral ABCD with AB = 6 cm, BC = 3 cm, AD = 4 cm, m ∠BAD = 120°, and m ∠ABC = 100°.
Explanation:
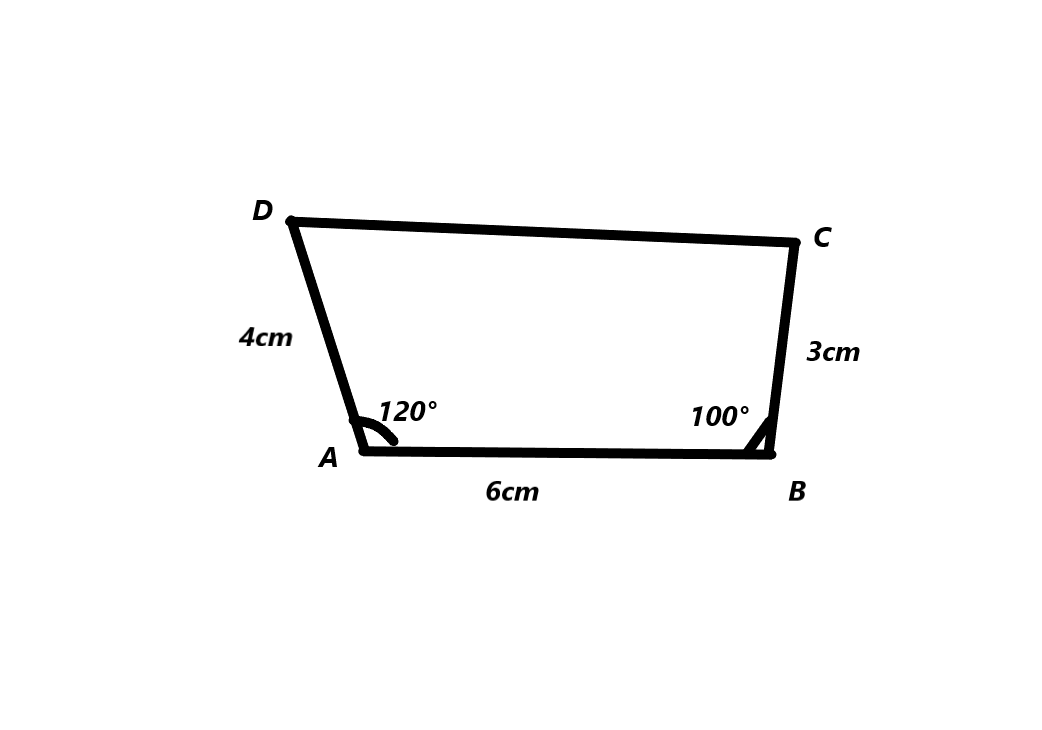
Answer:
The measurements of the quadrilateral ABCD is AB=6cm , BC=3cm , AD =4cm. The angle BAD= 120° angle ABC =100°.
b) Find the length of \(\overline{C D}\).
Answer:
The length of overline CD=10cm.
c) Label the midpoints of the four sides of this quadrilateral as W, X, Y, and Z. Join them to form quadrilateral WXYZ.
Answer:
Explanation:
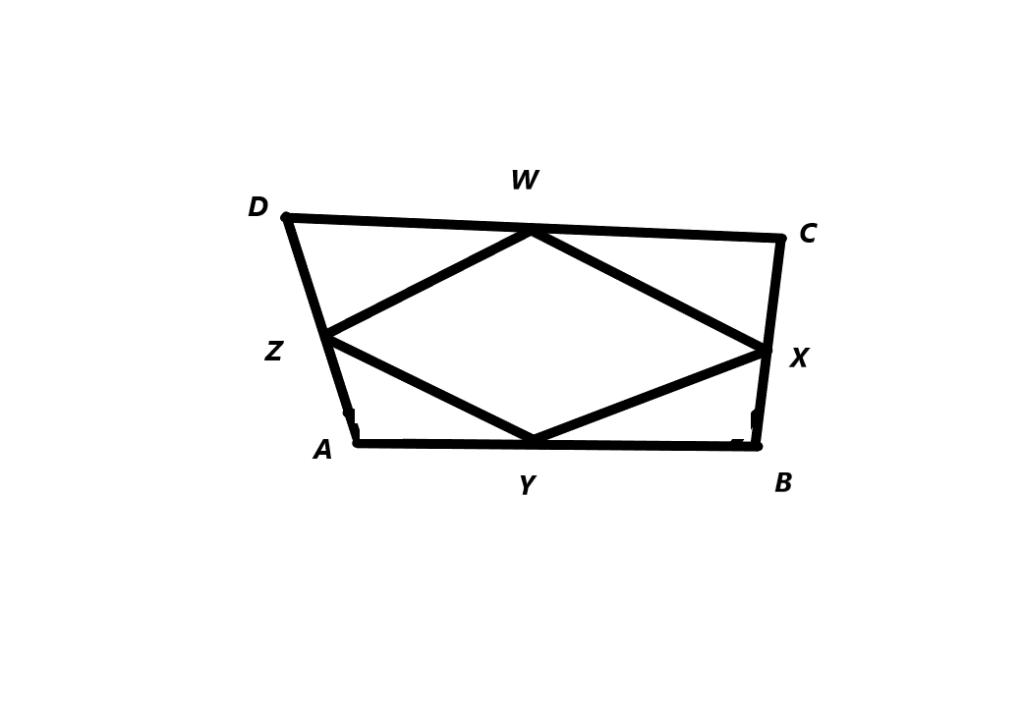
d) Compare the lengths of \(\overline{W X}\) and \(\overline{Y Z}\) . Compare the lengths of \(\overline{X Y}\) and \(\overline{W Z}\). What do you notice?
Answer:
Measure WX, YZ, XY, WZ:
WX ≈ 3.6 cm
YZ ≈ 3.6 cm
XY ≈ 4.4 cm
WZ ≈ 4.4 cm
We notice that we have:
WX = YZ
XY = WZ
Question 12.
Construct parallelogram PQRS with PQ = 6 cm, a height of 4.5 centimeters and interior angles 45° and 135°.
Explanation:
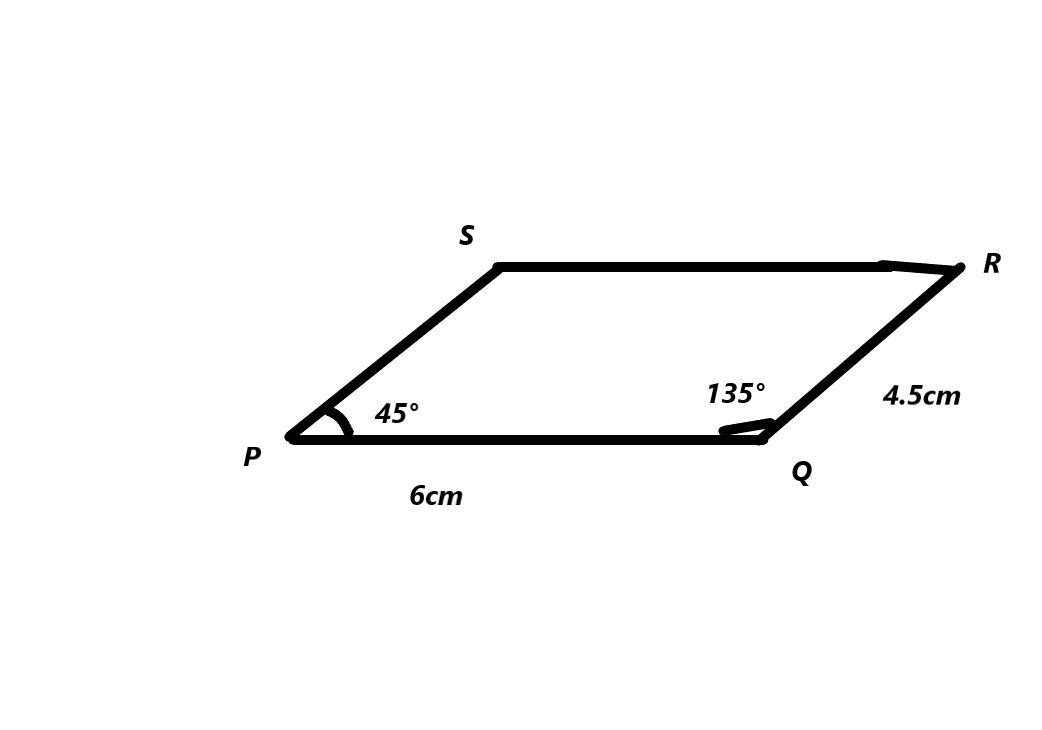
Answer:
The measurements of the parallelogram PQRS with PQ =6cm and height= 4.5cm.
The interior angles are 45° and 135°.
Question 13.
Draw rhombus ABCD with AC = 5 cm and AB = 6.5 cm. Also draw diagonal \(\overline{B D}\). How are the two diagonals related to each other? Explain.
Answer:
Explanation:
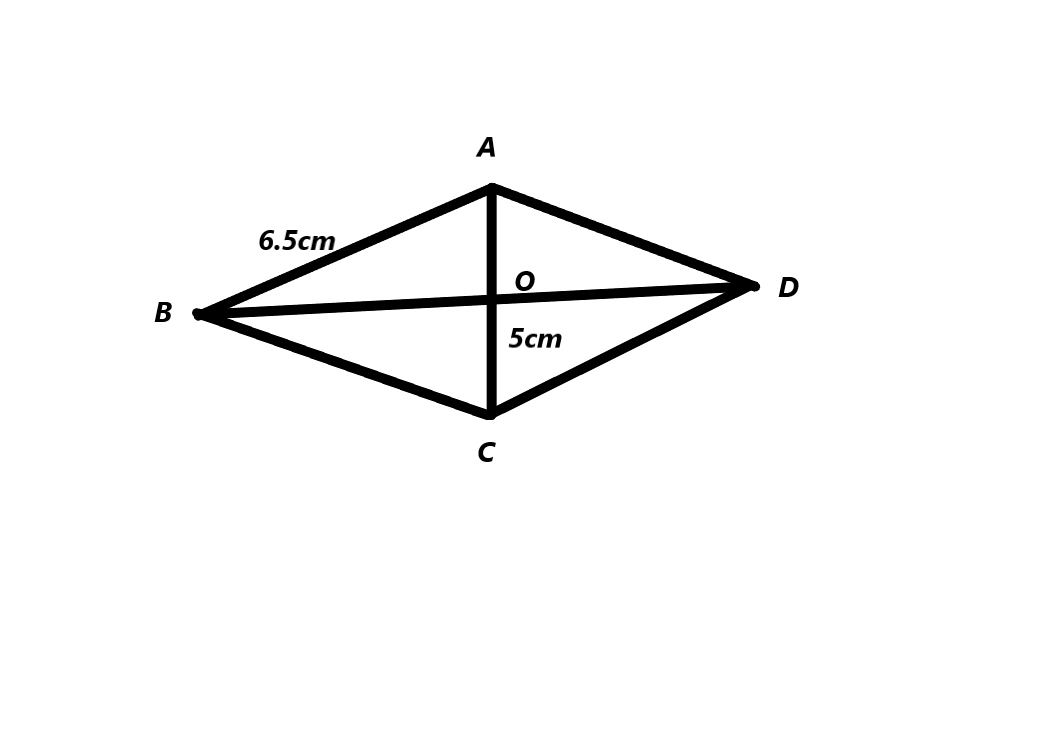
let ABCD be a rhombus whose diagonal AC and BD are intersecting at point O. We know that the diagram of parallelogram bisect at each other.
OA=OC and OB=OD
angle COB= angle COD
angle COB+ angle COD= 180°
angle COB=angle COD= 90°.
Question 14.
Jenny plans to make a trapezoidal bookmark for each of her teachers. The top will be 5 centimeters long and have right angles at either end. The right side will be 12 centimeters long, and the bottom of the bookmark will make a 50° angle with this side. Construct a template for Jenny’s bookmark. How long is the left side of Jenny’s template to the nearest centimeter?
Answer:
Explanation:
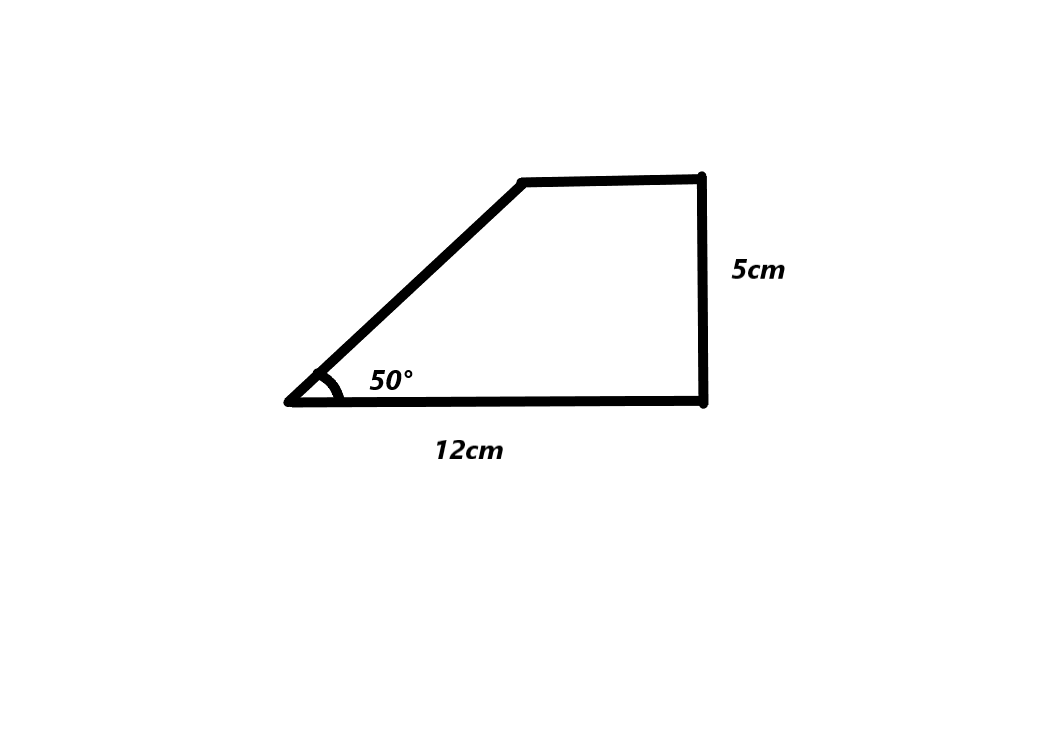
The measurements of the trapezoid length is 5cm and breadth is 12 cm. The bottom of the book mark angle is 50°. The left side of the jenny’s template is 4cm.
Question 15.
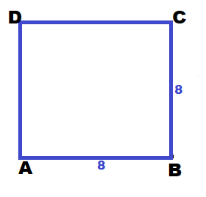
Martha plans to cut squares of paper from a roll of wrapping paper. She will package the squares to sell as origami papers to raise funds for a charity. If the area of the square paper is 64 square centimeters, construct the square Martha can use as a template.
Answer:
Determine the length of the square side:
AB2 = 64
AB = \(\sqrt{64}\) = 8
Sketch the rectangle:
Use a ruler to draw \(\overline{A B}\) so that is 7 cm long.
Using a protractor, draw ∠B with a measure of 90°.
Because BC = 5 cm, set the compass to a radius of 5 cm. Then using B as the center, draw an arc intersecting the ray drawn in previous step. Label this point of intersection as C. Because AD = 5 cm, use the same compass setting. Using A as the center, draw an arc:
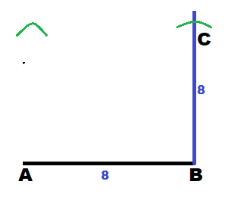
Because CD = 7 cm, set the compass to a radius of 7 cm. Then using C as the center draw an arc intersecting the ray drawn in previous step. Label this point of intersection as D.
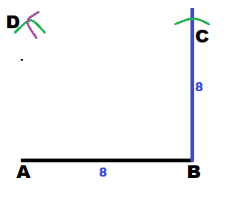
Draw \(\overline{C D}\) and \(\overline{A D}\)
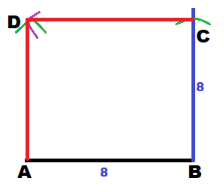
Question 16.
Jessie plans to make a patchwork pattern from colored paper by repeating a rhombus whose diagonals measure 4 centimeters and 5 centimeters. Use the given dimensions to construct a template for the rhombus.
Answer:
We have to construct the rhombus ABCD.
AC = 4
BD = 5
Sketch the rhombus:
Use a ruler to draw \(\overline{A C}\) so that is 4 cm long.

Draw the perpendicular bisector of \(\overline{A C}\):
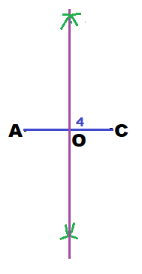
Because OB = OD = \(\frac{5}{2}\) = 2.5 cm, use the compass setting 2.5 cm. Then using O as the center, draw an arc to intersect the perpendicular bisector in the points B and D.
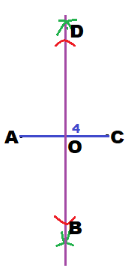
Draw \(\overline{A B}\), \(\overline{B C}\), \(\overline{C D}\) and \(\overline{D A}\).