Math in Focus Grade 7 Chapter 7 Lesson 7.5 Answer Key Understanding Scale Drawings

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 7 Lesson 7.5 Understanding Scale Drawings to score better marks in the exam.

Math in Focus Grade 7 Course 2 B Chapter 7 Lesson 7.5 Answer Key Understanding Scale Drawings

Math in Focus Grade 7 Chapter 7 Lesson 7.5 Guided Practice Answer Key

Calculate the scale factor.

Question 1.
In the diagram, trapezoid B has been enlarged to produce trapezoid A. Find the scale factor.

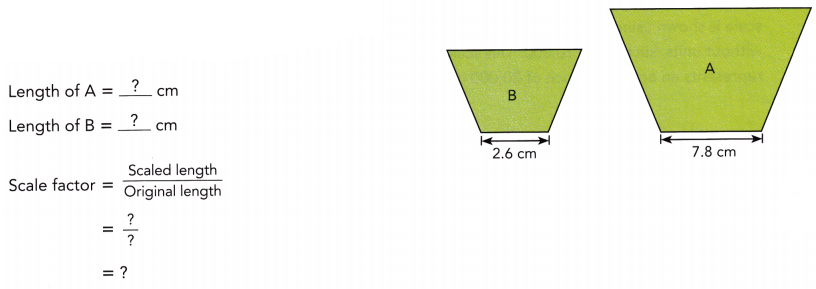
Answer:
3 cm

Explanation:
Length of A = 7.8 cm
Lenght of B = 2.6 cm
Scaled length = 7.8 cm
Original lenght = 2.6 cm
Scale factor = \(\frac{7.8}{2.6}\)
= 3 cm

 

 

 

 

 

 

 

 

Hands-On Activity

Redraw A Given Figure On Grid Paper At A Different Scale

Materials:

• different sizes of grid paper
• ruler

Work in pairs.

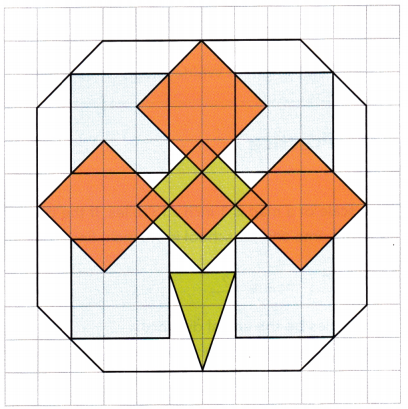
The drawing shows a figure formed by nine squares and a triangle enclosed in a polygon. You can use different-sized grids to produce the same drawing at different scales.

Step 1.
Use two different-sized grids. Redraw the figure on one grid. Have your partner redraw the figure on another grid.

Step 2.
Use a ruler to measure a length in the original drawing. Measure the corresponding length in your scale drawings. Then find the scale factor for each drawing. You can use the following to calculate the scale factor:

Complete.

Question 2.
The scale of a map is 1 inch : 15 miles. If the distance on the map between John’s home and his school is 0.6 inch, find the actual distance in miles.

Answer:
The actual distance is 9 miles.

Explanation:

 

 

 

 

 

 

 

 

 

Complete.

Question 3.
The actual distance between Boston and New York is 220 miles. The scale on a particular map is 1 inch : 25 miles. How far apart on the map are the two cities? 1 inch : 25 miles means 1 inch on the map represents 25 miles on the ground.
Let x inches be the length on the map.

Answer:
8.8 inches

Question 4.
A model car is built using a scale of 1: 18. The length of the model car is 12 inches. Find the actual length of the car in feet.
Answer:
Let x be the actual length of the car in inches.
1: 18 = Scaled length of the car: Actual length of the car
We have:
Substitute values:
1 : 18 = 12 : x
Write ratios in fraction form:
\(\frac{1}{18}\) = \(\frac{12}{x}\)
Write cross products:
x = 18 × 12
Simplify the x.
x = 216
Now convert to feet:
12 in = 1 ft
216 in = \(\frac{1}{12}\) × 216
= 18 ft
The actual length of the car is 18 feet.

Hands-On Activity

Investigate The Relationship Between The Scale Factor And Its Corresponding Area

Work individually.

A square that has a side length of 1 centimeter has an area of 1 square centimeter. In this activity, you will explore how enlarging such a square by a scale factor affects its area.

Step 1.
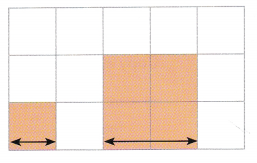
Suppose you enlarge the square by a factor of 2. Find the side length and the area of the resulting square.

Length of square = cm
(twice the original length)
Area of square = cm²
(increased by a factor of 4)
Answer:
Length of square is 4 cm.
Area of square = 16 cm²

Explanation:
The original length is 2 cm.
Now the lenght of square is 2 + 2 = 4 cm.
Therefore the length of square is 4 cm.
And area of the square is = 4 × 4 = 16 cm²

Step 2.
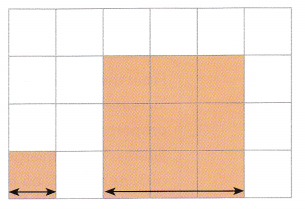
Suppose you enlarge the square by a factor of 3. Find the side length and the area of the resulting square.
Length of square = cm
(three times the original length)

Area of square = cm²
(increased by a factor of 9)
Answer:
Length of square is 9 cm.
Area of square = 9 × 9 = 18 cm²

Explanation:
Original length of the square is 3 cm.
New length of the square is 3 + 3 = 6 cm.
Area of the square = 6 × 6 = 36 cm²

Step 3.
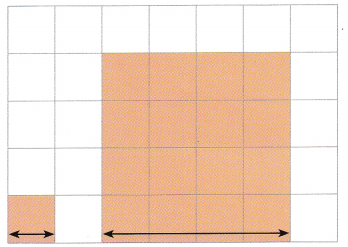
Suppose you enlarge the square by a factor of 4. Find the side length and the area of the resulting square.
Length of square = cm
(four times the original length)

Area of square = cm²
(increased by a factor of )
Answer:
16 cm, 256 cm²

Explanation:
Given, Original length is 4 cm.
Now the new length of the square is 16 cm.
Area of the square is 16 × 16 = 256 cm²

Step 4.
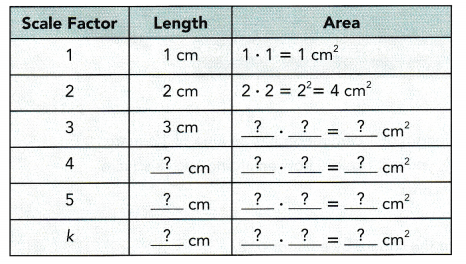
Copy and complete the table.

 

 

 

 

 

 

 

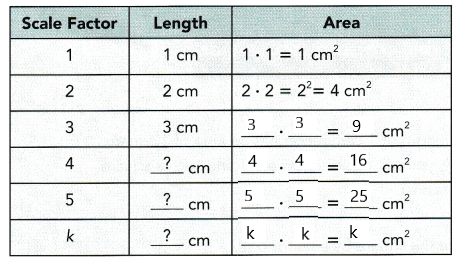
Copy and complete.

a) Increasing the length of a square by a factor of 5 increases the area by a factor of .
Answer:
Area by a factor is 25 cm²

b) Increasing the length of a square by a factor of k increases the area by a factor of .
Answer:
Area of the square is k² cm²  

Math Journal
Compare the side lengths and the areas for the various scale factors. What pattern do you observe?

From the above activity, the area of a square increases as the square of the scale factor. This property applies to other two-dimensional figures. If you enlarge a figure by a scale factor of 3, its area will be enlarged by a scale of 3² = 9

Complete.

Question 5.
Sylvia makes a map of her yard. On a map, 1 inch represents 8 feet. On the map, the area of a patch of grass is 12 square inches. Find the actual area of the patch of grass.

Answer:
1 inch : 8 feet means 1 inch on the map represents 8 feet on the ground.
Map length : Actual length = 1 in. : 8 ft
Map area: Actual area = 1 in.² : 8² ft²
Let y represent the actual area of the patch of grass in square feet.
Write a proportion:
\(\frac{\text { Area of patch of grass on map }}{\text { Actual area of patch of grass }}=\frac{1}{64}\)
Substitute:
\(\frac{12}{y}\) = \(\frac{1}{64}\)
Write the cross products:
y = 12 · 64
Simplify
y = 768
The actual area of the grass patch is 768 square feet.

Copy and complete.

Question 6.
A blueprint is a type of scale drawing used by architects. An architect is making a blueprint for a conference room that will have a floor area of 196 square feet. If the scale on the blueprint is 1 inch : 7 feet, find the area of the conference room floor on the blueprint.

Let y represent the area of the conference room on the blueprint in square inches.

Answer:
1 inch : 7 feet means 1 inch on the bLueprint represents 7 feet on the ground.
Blueprint length : ActuaL Length = 1 in. : 7 ft
Blueprint area : Actual area = 1 in.² : 7² ft²
Let y represent the area of the conference room on the blueprint in square inches.
Write a proportion:
\(\frac{\text { Area of room on blueprint }}{\text { Actual area of room }}=\frac{1}{49}\)
Substitute:
\(\frac{y}{196}\) = \(\frac{1}{49}\)
Write the cross products:
49y = 196
Divide both sides by 49:
\(\frac{49y}{49}\) = \(\frac{196}{49}\)
Simplify:
y = 4
The gloor area of the conference room on the blueprint is 4 square inches.

Math in Focus Course 2B Practice 7.5 Answer Key

Solve. Show your work.

Question 1.
A model of a ship is 6 inches long. The actual ship is 550 feet (6,600 inches). Find the scale factor used for the model.

Answer:
We are given:
Model length: 6 in.
Actual length: 6,600 in.
Determine the scale factor used for the model:
Scale factor: \(\frac{\text { Model length }}{\text { Actual length }}\) = \(\frac{6}{6,600}\)
= \(\frac{1}{1,100}\)

Question 2.
On a blueprint, the length of a wall is 5 inches. The actual length of the wall is 85 feet. What scale is used for the blueprint?
Answer:
We are given:
Blueprint length: 5 in.
Actual length: 85 ft
Convert the actual length from feet to inches:
1 ft = 12 in.
85 ft = (85 · 12) in. = 1020 in.
Determine the scale factor used for the blueprint:
Scale factor: \(\frac{\text { Blueprint length }}{\text { Actual length }}\) = \(\frac{5}{1020}\)
= \(\frac{1}{204}\)

Question 3.
An artist made a painting of a water pitcher. Then the artist reduced the size of the painting. Find the scale factor of the reduction.

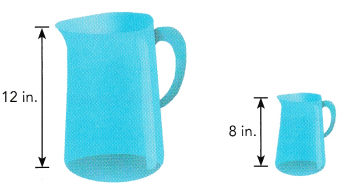
Answer:
We are given:
Big size: 12 in.
Reduced size: 8 in.
Determine the scale factor of reduction:
Scale factor: \(\frac{\text { Reduced size }}{\text { Big size }}\) = \(\frac{8}{12}\)
= \(\frac{2}{3}\)

Question 4.
The height of a building in a drawing is 15 inches. If the actual height of the building is 165 feet, find the scale factor of the drawing.
Answer:
We are given:
Drawing height: 15 in.
Actual height: 165 ft
Convert feet to inches:
1 ft = 12 in.
165 ft = (165 · 12) in. = 1980 in.
Determine the scale factor:
Scale factor: \(\frac{\text { Drawing height }}{\text { Actual height }}\) = \(\frac{15}{1980}\)
= \(\frac{1}{132}\)

Question 5.
In a scale drawing, a sofa is 3 inches long. If the actual length of the sofa ¡s 5 feet long, find the scale factor.
Answer:
We are given:
Drawing length: 3 in.
Actual length: 5 ft
Convert feet to inches:
1ft = 12 in.
5 ft = (5 · 12) in. = 60 in.
Determine the scale factor:
Scale factor: \(\frac{\text { Drawing length }}{\text { Actual length }}\) = \(\frac{3}{60}\)
= \(\frac{1}{60}\)

Question 6.
Daniel is making a scale drawing of his classroom for a project. The length of his classroom is 30 feet long. In his drawing, the length of the classroom is 6 inches. Find the scale factor of Daniel’s drawing.
Answer:
We are given:
Drawing length: 6 in.
Actual length: 30 ft
Convert feet to inches:
1 ft = 12 in.
30 ft = (30 · 12) in. = 360 in.
Determine the scale factor:
Scale factor: \(\frac{\text { Drawing height }}{\text { Actual height }}\) = \(\frac{6}{360}\)
= \(\frac{1}{60}\)

Question 7.
Two cities are 7 inches apart on a map. If the scale of the map is 0.5 inch : 3 miles, what is the actual distance between the two cities?
Answer:
0.5 inch : 3 miles means 0.5 inches on the map represents 3 miles on the ground.
Let x miles be the actual distance.
We have:
0.5 inches : 3 miles = 7 inches: x miles
Write ratios in fraction form:
\(\frac{0.5 \mathrm{in}}{3 \mathrm{mi}}\) = \(\frac{7 \mathrm{in}}{x \mathrm{mi}}\)
Write without units:
\(\frac{0.5}{3}\) = \(\frac{7}{x}\)
Write cross products:
0.5x = 3 · 7
Simplify:
0.5x = 21
Multiply both sides by 2:
x = 42
The actual distance is 42 miles.

Question 8.
A road map of New Orleans uses a scale of 1 inch : 3 miles. If Carlton Avenue is 1 .3 inches long on the map, what is the actual length of the street?
Answer:
1 inch : 3 miles means 1 inch on the map represents 3 miles on the ground
Let x miles be the actual distance.
We have:
1 inch : 3 miles = 13 inches : x miles
Write ratios in fraction form:
\(\frac{1 \mathrm{in} .}{3 \mathrm{mi}}\) = \(\frac{1.3 \mathrm{in} .}{x \mathrm{mi}}\)
Write without units:
\(\frac{1}{3}\) = \(\frac{1.3}{x}\)
Write cross products:
x = 3 · 1.3
Simplify:
x = 3.9
The actual distance is 3.9 miles.

Question 9.
The scale of a map is 1 inch : 85 miles.
a) On the map, the river is 14 inches long. Find the actual length of the river in miles.
Answer:
1 inch : 85 miles means 1 inch on the map represents 85 miles on the ground.
Let x miles be the actuaL length.
We have:
1 inch : 85 miles = 14 inches : x miles
Write ratios in fraction form:
\(\frac{1 \mathrm{in}}{85 \mathrm{mi}}\) = \(\frac{14 \mathrm{in} .}{x \mathrm{mi}}\)
Write without units:
\(\frac{1}{85}\) = \(\frac{14}{x}\)
Write cross products:
x = 85 · 14
Simplify:
x = 1,190
The actual length is 1,190 miles.

b) The actual distance between two towns is 765 miles. Find the distance on the map between these towns.
Answer:
Let y inches be the distance on the map.
We have:
1 inch : 85 miles = y inches : 765 miles
Write ratios in fraction form:
\(\frac{1 \mathrm{in} .}{85 \mathrm{mi}}\) = \(\frac{y \mathrm{in}}{765 \mathrm{mi}}\)
Write without units:
\(\frac{1}{85}\) = \(\frac{y}{765}\)
Write cross products:
85y = 765
Divide both sides by 85.
\(\frac{85y}{85}\) = \(\frac{765}{85}\)
Simplify:
y = 9
The distance on the map is 9 inches.

Question 10.
Goodhope River is 48 miles long. What is the length of the river on a map with a scale of 1 inch : 15 miles?
Answer:
1 inch : 15 miles means 1 inch on the map represents 15 miles on the ground.
Let x inches be the length on the map.
We have:
1 inch : 15 miles = x inches : 48 miles
Write ratios in fraction form:
\(\frac{1 \mathrm{in} .}{15 \mathrm{mi}}\) = \(\frac{x \mathrm{in}}{48 \mathrm{mi}}\)
Write without units:
\(\frac{1}{15}\) = \(\frac{x}{48}\)
Write cross products:
15x = 4
Divide both sides by 15:
\(\frac{15x}{15}\) = \(\frac{48}{15}\)
Simplify:
x = 3.2
On the map the length is 3.2 inches.

Question 11.
A map is drawn using a scale of 1 inch : 165 miles. The length of a road on the map is 12 inches. Find the actual length of the road.
Answer:
1 inch : 165 miles means 1 inch on the map represents 165 mites on the ground.
Let x mites be the actual length.
We have:
1 inch : 165 miles = 12 inches : x miles
Write ratios in fraction form:
\(\frac{1 \mathrm{in}}{165 \mathrm{mi}}\) = \(\frac{12 \mathrm{in} .}{x \mathrm{mi}}\)
Write without units:
\(\frac{1}{165}\) = \(\frac{12}{x}\)
Write cross products:
x = 165 · 12
Simplify:
x = 1980
The actual length of the road is 1980 miles.

Question 12.
On a particular map, 2 inches represents an actual distance of 64 miles. Towns A and B are 608 miles apart. Find the distance between the two towns, in inches, on the map.
Answer:
2 inches : 64 miles means 2 inches on the map represents 64 mites on the ground.
Let x inches be the distance on the map.
We have:
2 inches : 64 miles = x inches : 608 miles
Write ratios in fraction form:
\(\frac{2 \mathrm{in}}{64 \mathrm{mi}}\) = \(\frac{x \text { in. }}{608 \mathrm{mi}}\)
Write without units:
\(\frac{2}{64}\) = \(\frac{x}{608}\)
Write cross products:
64x = 2 · 608
64x = 1,216
Divide both sides by 64.
\(\frac{64x}{64}\) = \(\frac{1,216}{64}\)
Simplify:
x = 19
On the map the two cities are 19 inches apart.

Question 13.
On a particular map, 1 inch represents an actual distance of 2.5 miles. The actual area of a lake is 12 square miles. Find the area of the lake on the map.
Answer:
1 inch : 2.5 miles means 1 inch on the map represents 2.5 miles on the ground.
Map length : Actual length = 1 in. : 2.5 mi.
Map area : Actual area = 1 in.² : 2.5² mi.²
Let y represent the area of the lake on map in square inches.
Write a proportion:
\(\frac{\text { Area of lake on map }}{\text { Actual area of lake }}=\frac{1}{6.25}\)
Substitute:
\(\frac{y}{12}\) = \(\frac{1}{6.25}\)
Write the cross products
6.25y = 12
Divide both sides by 6.25 and simplify:
\(\frac{6.25y}{6.25}\) = \(\frac{12}{6.25}\)
y = 1.92
The area of the lake on the map is 1.92 square inches.

Question 14.
On the map, the area of a nature preserve is 54.2 square inches. If the scale of the map is 1 inch : 8 miles, find the actual area of the nature preserve.
Answer:
1 inch : 8 miles means 1 inch on the map represents 8 miles on the ground.
Map Length : Actual length = 1 in. : 8 mi.
Map area: Actual area = 1 in.² : 8² mi.²
Let y represent the actual area of the nature preserve in square miles.
Write a proportion:
\(\frac{\text { Area of nature preserve on map }}{\text { Actual area of nature preserve }}=\frac{1}{64}\)
Substitute:
\(\frac{54.2}{y}\) = \(\frac{1}{64}\)
Write the cross products:
y = 54.2 × 64
Simplify:
y = 3,468.8
The actual area of the nature preserve is 3,468.8 square miles.

Question 15.
The map shows two roads labeled A and B.

a) Using a ruler, measure, in centimeters, the lengths of roads A and B.

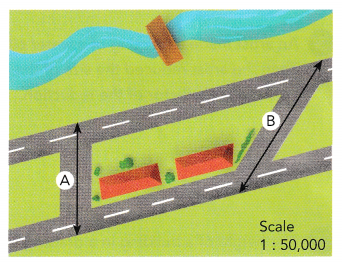
Answer:
We measure the lengths of the roads A and B, in centimeters, using a ruler:
Length A = 24 cm
Length B = 3.3 cm

b) Using the scale given, find, in kilometers, the actual lengths of roads A and B.
Answer:
We are given the scale:
1 : 50,000
We determine the actual length x of Road A in centimeters:
\(\frac{2.4}{x}\) = \(\frac{1}{50,000}\)
x = 2.4 · 50,000
= 120,000 cm
Convert to kilometers:
1 km = 1000 m = 100,000 cm
120,000 cm = \(\frac{120,000}{100,000}\) km = 1.2 km
We determine the actual length y of Road B in centimeters:
\(\frac{3.3}{y}\) = \(\frac{1}{50,000}\)
y = 3.3 · 50,000
= 165,000 cm
Convert to kilometers:
1 km = 1000 m = 100,000 cm
165,000 cm = \(\frac{165,000}{100,000}\) km = 1.65 km

Question 16.
The map shows seven cities in Florida. Using the scale on the map, use a ruler to measure the distance between the following pairs of cities. Then find the actual distance between them in miles.

a) Orlando and West Palm Beach
Answer:
We measure the lengths of the distance between Orlando and West Palm Beach, in centimeters, using a ruler:
Length Orlando-West Pam Beach = 3 cm
Length Fort Myers-Miami Beach = 24 cm
We are given the scale:
1 cm : 50 miles
We determine the actual distance x between Orlando and West Palm Beach in centimeters:
\(\frac{3}{x}\) = \(\frac{1}{50}\)
x = 3 · 50
= 150 miles

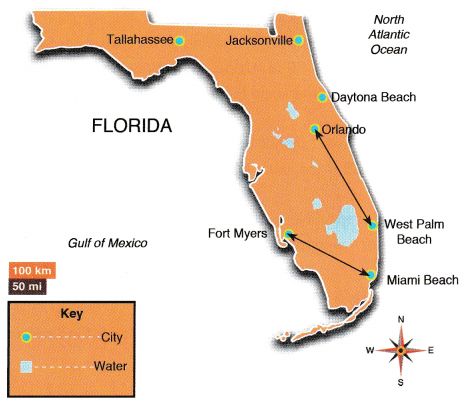
b) Fort Myers and Miami Beach
Answer:
We determine the actual distance y between Fort Myers and Miami Beach in centimeters:
\(\frac{2.4}{y}\) = \(\frac{1}{50}\)
x = 2.4 · 50
= 120 miles

Question 17.
Use the scale on the floor plan of a house to find each of the following.
a) The actual length and width of room 1.
Answer:
2 cm : 5 m means 2 cm on the plan represent 5 m on the ground.
Let x, y meters be the actual length and width of room 1.
We have:
2 cm : 5 m = 1.8 cm : x m
Write ratios in fraction form:
\(\frac{2 \mathrm{~cm}}{5 \mathrm{~m}}\) = \(\frac{1.8 \mathrm{~cm}}{x \mathrm{~m}}\)
Write without units:
\(\frac{2}{5}\) = \(\frac{1}{2}\)
Write cross products:
2x = 5 · 1.8
Divide by 2 and simplify:
\(\frac{2x}{x}\) = \(\frac{9}{2}\)
x = 4.5 meters
We do the same to find the actual width:
2 cm : 5 m = 1.4 cm : y m
\(\frac{2 \mathrm{~cm}}{5 \mathrm{~m}}\) = \(\frac{1.4 \mathrm{~cm}}{y \mathrm{~m}}\)
\(\frac{2}{5}\) = \(\frac{1.4}{y}\)
2y = 5 · 1.4
\(\frac{2y}{2}\) = \(\frac{7}{2}\)
y = 3.5 meters

b) The width of the door on the floor plan if its actual width is 0.8 meter.
Answer:
We determine the width z of the door on the floor plan:
\(\frac{2 \mathrm{~cm}}{5 \mathrm{~m}}\) = \(\frac{z \mathrm{~cm}}{0.8 \mathrm{~m}}\)
\(\frac{2}{5}\) = \(\frac{z}{0.8}\)
5z = 2 · 0.8
\(\frac{5z}{5}\) = \(\frac{1.6}{5}\)
z = 0.32 cm

c) The actual area of the floor of the house to the nearest square meter

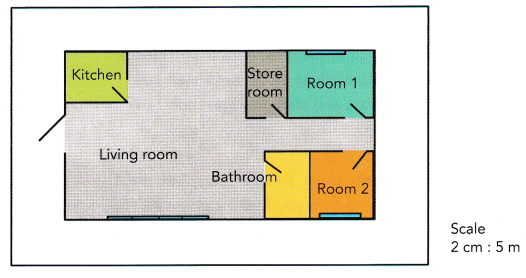
Answer:
We have:
Length scale: 2 cm : 5 m
Area scale: 2² cm² : 5² m²
We determine the actual area s of the floor:
\(\frac{4}{25}\) = \(\frac{7.6 \cdot 3}{s}\)
4s = 25 · 22.8
\(\frac{4s}{4}\) = \(\frac{570}{4}\)
s ≈ 143 m²

Question 18.
A tower is drawn using a scale of 1 inch : 3 feet. The height of the tower in the drawing is 1 foot 5 inches. Then, an architect decides to make a new scale drawing of the tower. In the new scale, the scale is 1 inch : 5 feet. Find the height of the tower in the new drawing.
Answer:
1 inch : 3 feet means 1 inch on the drawing represents 3 feet on the ground.
Let x miles be the actual height
We have:
1 inch : 3 feet 1 ft 5 in. : x feet
Write ratios in fraction form:
\(\frac{1 \mathrm{in} .}{3 \mathrm{ft}}\) = \(\frac{(12+5) \mathrm{in} .}{x \mathrm{ft}}\)
Write without units:
\(\frac{1}{3}\) = \(\frac{17}{x}\)
Write cross products:
x = 3 · 17
Simplify
x = 51 ft
The actual height of the tower is 51 ft.
The new scale is 1 inch : 5 feet
We determine the height y of the tower in the new drawing:
\(\frac{1 \mathrm{in} .}{5 \mathrm{ft}}\) = \(\frac{y \mathrm{in} .}{51 \mathrm{ft}}\)
\(\frac{1}{5}\) = \(\frac{y}{51}\)
5y = 51
\(\frac{5y}{5}\) = \(\frac{51}{5}\)
y = 10.2 inches

Question 19.
Each student walked in a straight line from one point to another. Use a centimeter ruler to measure distances on the map shown. Use the scale on the map to find the distance each student walked in meters.

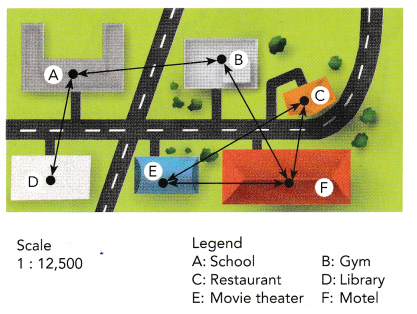
We measure the lengths of the roads, in centimeters, using a ruler:
Length DA = 1.8 cm
Length AB = 3.3 cm
Length BF = 2.5 cm
Length CF = 1.4 cm
Length EF = 2.8 cm
Length CE = 3.5 cm

a) Ethan walked from the library to the school, and then to the gym.
Answer:
We are given the scale:
1 : 12,500
We determine the actual length x Ethan walked:
\(\frac{D A+A B}{x}\) = \(\frac{1}{12,500}\)
\(\frac{1.8+3.3}{x}\) = \(\frac{1}{12,500}\)
x = 5.1 · 12,500
= 63,750 cm
Convert to meters:
1 m = 100 cm
63,750 cm = \(\frac{63,750}{100}\) m = 637.5 m

b) Joshua walked from the motel to the restaurant, and then to the movie theater.
Answer:
We determine the actual length y joshua walked:
\(\frac{F C+C E}{y}\) = \(\frac{1}{12,500}\)
\(\frac{1.4+3.5}{y}\) = \(\frac{1}{12,500}\)
x = 4.9 · 12,500
= 61,250 cm
Convert to meters:
1 m = 100 cm
61,250 cm = \(\frac{61,250}{100}\) m = 612.5 m

c) Chloe walked from the gym to the motel, and then to the movie theater.
Answer:
We determine the actual length z Chloe walked:
\(\frac{B F+F E}{z}\) = \(\frac{1}{12,500}\)
\(\frac{2.5+2.8}{z}\) = \(\frac{1}{12,500}\)
x = 5.3 · 12,500
= 66,250 cm
Convert to meters:
1 m = 100 cm
66,250 cm = \(\frac{66,250}{100}\) m = 662.5 m

Brain @ Work

Question 1.
You know you can bisect any angle using a compass and a straightedge. Geometers have known for thousands of years that it is impossible to trisect any given angle using a compass and straightedge. (The word trisect means to divide into three equal parts.) But it is possible to trisect certain angles, including a right angle. Using only a compass and straightedge, show how you can draw a right angle that is trisected.
Answer:
We are given the right angle:
m∠AOB – 90°

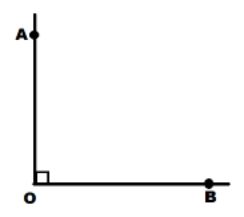
Use the compass: with the center in O, draw an arc. Labet its intersection with \(\overline{O A}\) and \(\overline{O B}\) by C and D

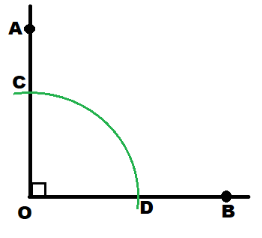
With the same radius place the compass in center C, then D and draw arcs which intersect the arc drawn in the previous step in N and M.

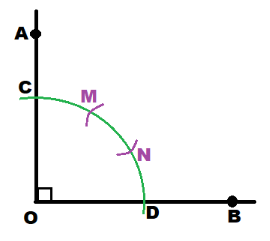
Use a ruler to draw \(\overrightarrow{O M}\) and \(\overrightarrow{O N}\).

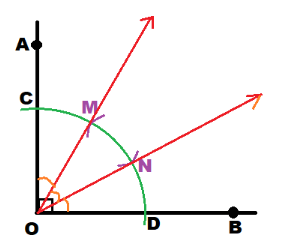
m∠AOM = m∠MON = m∠NOB
= \(\frac{m \angle A O B}{3}\) = \(\frac{90^{\circ}}{3}\) = 30°

Question 2.
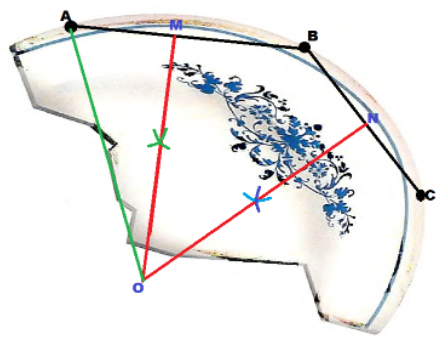
You accidentally broke your mother’s favorite plate. You want to ask an artist to reproduce it. You ask your math teacher to help you find the original size of the plate. She suggests that you locate three points on the rim of the plate and use the points to draw two segments. The point where the two perpendicular bisectors of these segments intersect will be the center of the plate. From that you can measure the radius. Copy and complete the diagram below. Then measure to find the diameter of the plate.

Answer:
We consider 3 points on the rim of the plate:

The center of the circle/plate is situated at the intersection of the perpendicular bisectors of \(\overline{A B}\) and \(\overline{B C}\).

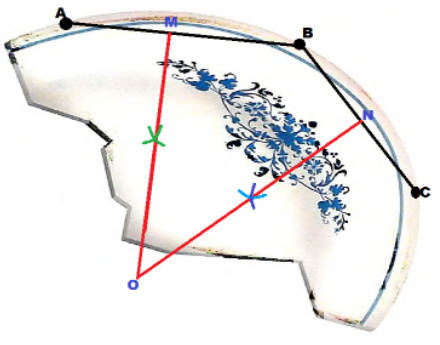
The radius of the circle/plate is OA.